对于快速热循环注塑工艺，由于填充阶段和保压阶段初期的模具型腔表面温度相对较高，与高温型腔壁接触的塑料熔体温度也较高，型腔侧塑料熔体尚未冷凝，故其收缩量很小，所以保压阶段初期较大的保压压力并不能起到很好的补缩作用，反而会导致塑件因厚度方向的保压不均而产生更大的翘曲变形。因此，在注塑保压阶段初期不宜采用较高的保压压力。针对这种基于单侧模具快速加热和快速冷却的快速热循环注塑工艺，可以采用一种初期低压慢速、后期高压快速的两段式反保压压力控制策略。初期较低的保压压力可使高温型腔侧的塑料熔体在冷却过程中首先产生一定量的收缩，使其与型腔壁间具备足够的间隙，为随后高保压压力提供充分的保压空间，以增强保压补缩效果，减小型腔侧塑料熔体的过量收缩，从而减小塑件的翘曲变形和表面缩痕。

利用表8-3给出的中心复合试验设计方案，研究两段式反保压模式对塑件翘曲变形和缩痕深度的影响。每个设计变量均包含5个水平，第一段保压压力（p₁）分别为2.5MPa、10MPa、25MPa、40MPa和47.5MPa，第二段保压压力（p₂）分别为52.7MPa、60MPa、75MPa、90MPa和97.5MPa，第一段保压时间（t₁）分别为0.75s、1.5s、3.0s、4.5s和5.25s，第二段保压时间（t₂）分别为3.0s、4.0s、6.0s、8.0s和9.0s，其他工艺参数与上一节中设定的工艺参数相同。另外，假定冷却前保压时间为0s，即模具冷却与保压是同时进行的。通过模拟分析发现，当第一段保压压力低于45MPa时，在V/P转换点塑料熔体容易发生回流，导致型腔填充不足。为此，在第一段保压之前又增加了一段保压时间为0.3s、保压压力为50MPa的保压阶段，以确保塑料熔体可以完全充满型腔，故在模拟分析中实际上采用的是三段式保压控制。

表8⁃3 四因素五水平中心复合试验设计方案及模拟计算结果

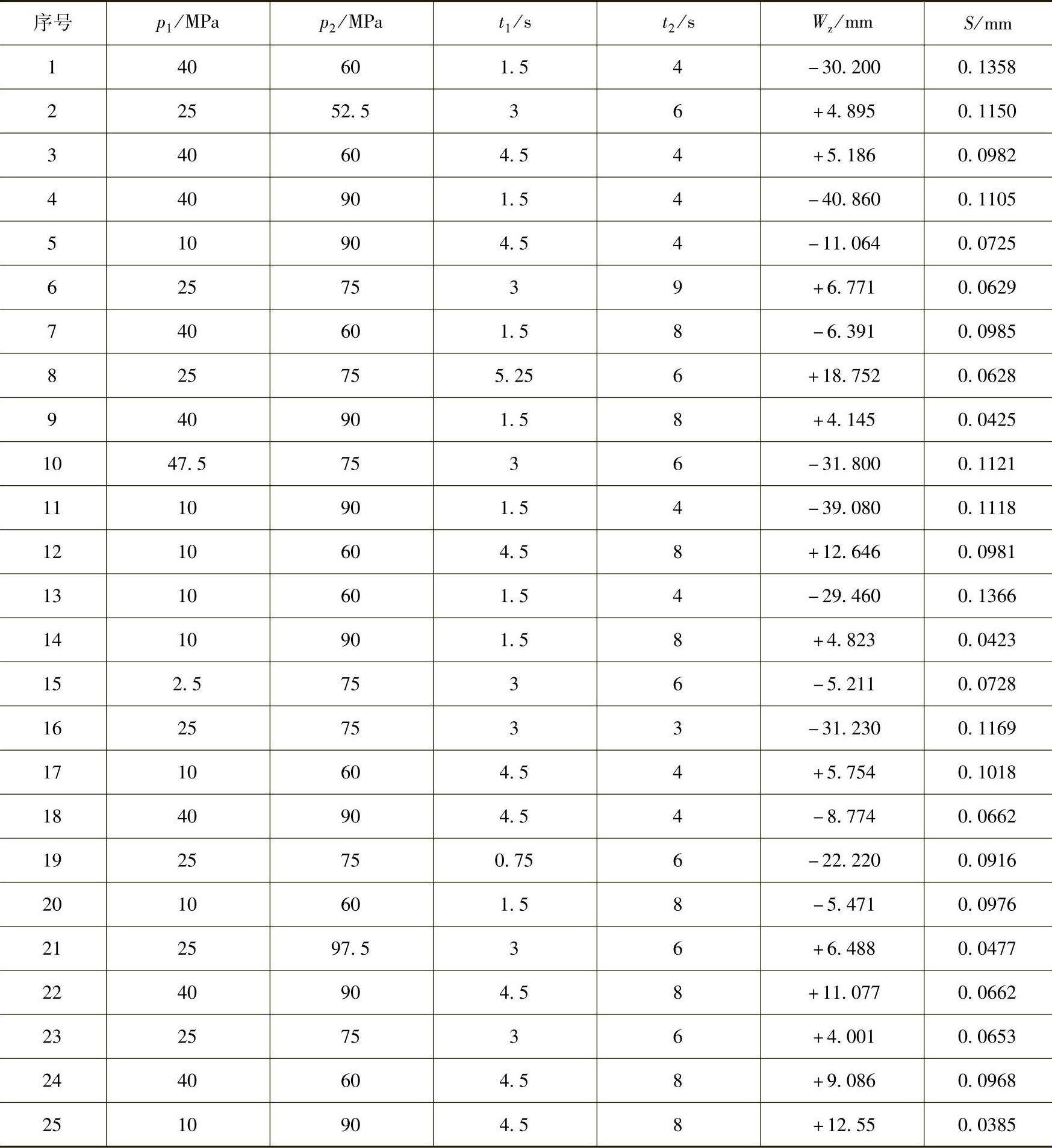
根据表中的工艺变量组合设定快速热循环注塑保压参数，执行快速热循环注塑工艺的填充、保压和翘曲模拟分析，模拟获得的塑件Z向最大翘曲变形量和最大缩痕深度见表8-3。表中，“+”表示塑件发生凸翘曲变形，而“-”则表示塑件发生凹翘曲变形，如图8-29所示。图8-30所示为模拟获得的多段保压工艺参数对翘曲变形的影响。从图中可以看出，在设计空间范围内，随着第一段保压压力增大，塑件翘曲变形量的绝对值先逐渐减小后又逐渐增大；而随着第二段保压压力增大，塑件翘曲变形量的绝对值则先逐渐增大后又逐渐减小；随着第一段保压时间增大，塑件翘曲变形量的绝对值先快速减小后又逐渐增大；而随着第二段保压时间增大，塑件翘曲变形量的绝对值也先快速减小后又逐渐增大。图8-31所示为模拟获得的多段保压工艺参数对缩痕深度的影响。从图中可以看出，在设计空间范围内，随着第一段保压压力增大，塑件缩痕深度逐渐增大；而随着第二段保压压力增大，塑件缩痕深度则逐渐减小；随着第一段或第二段保压时间增加，塑件缩痕深度均逐渐减小。

图8-29 液晶电视机面板的凸翘曲变形和凹翘曲变形

a）凸翘曲变形 b）凹翘曲变形

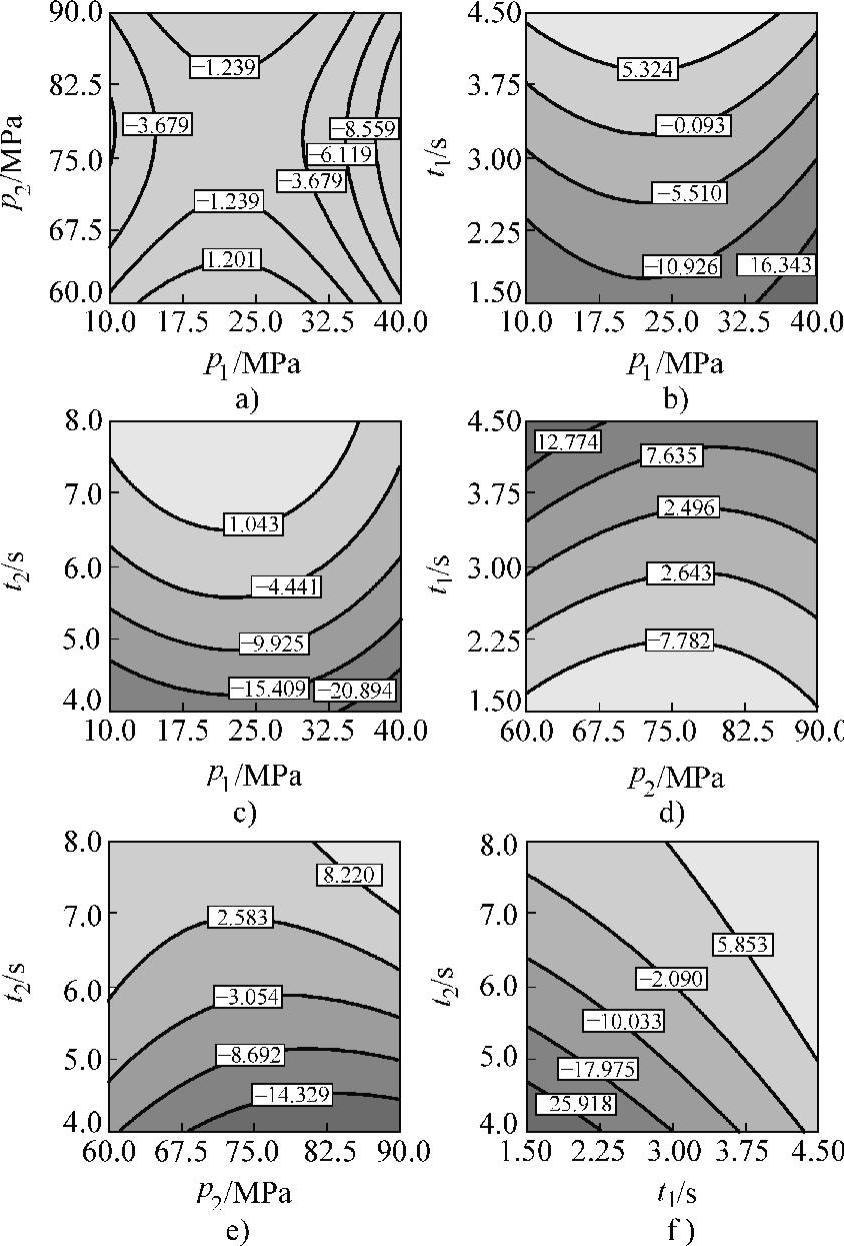
图8-30 模拟获得的多段保压工艺参数对翘曲变形的影响

a）p₁和p₂ b）p₁和t₁ c）p₁和t₂ d）p₂和t₁ e）p₂和t₂ f）t₁和t₂

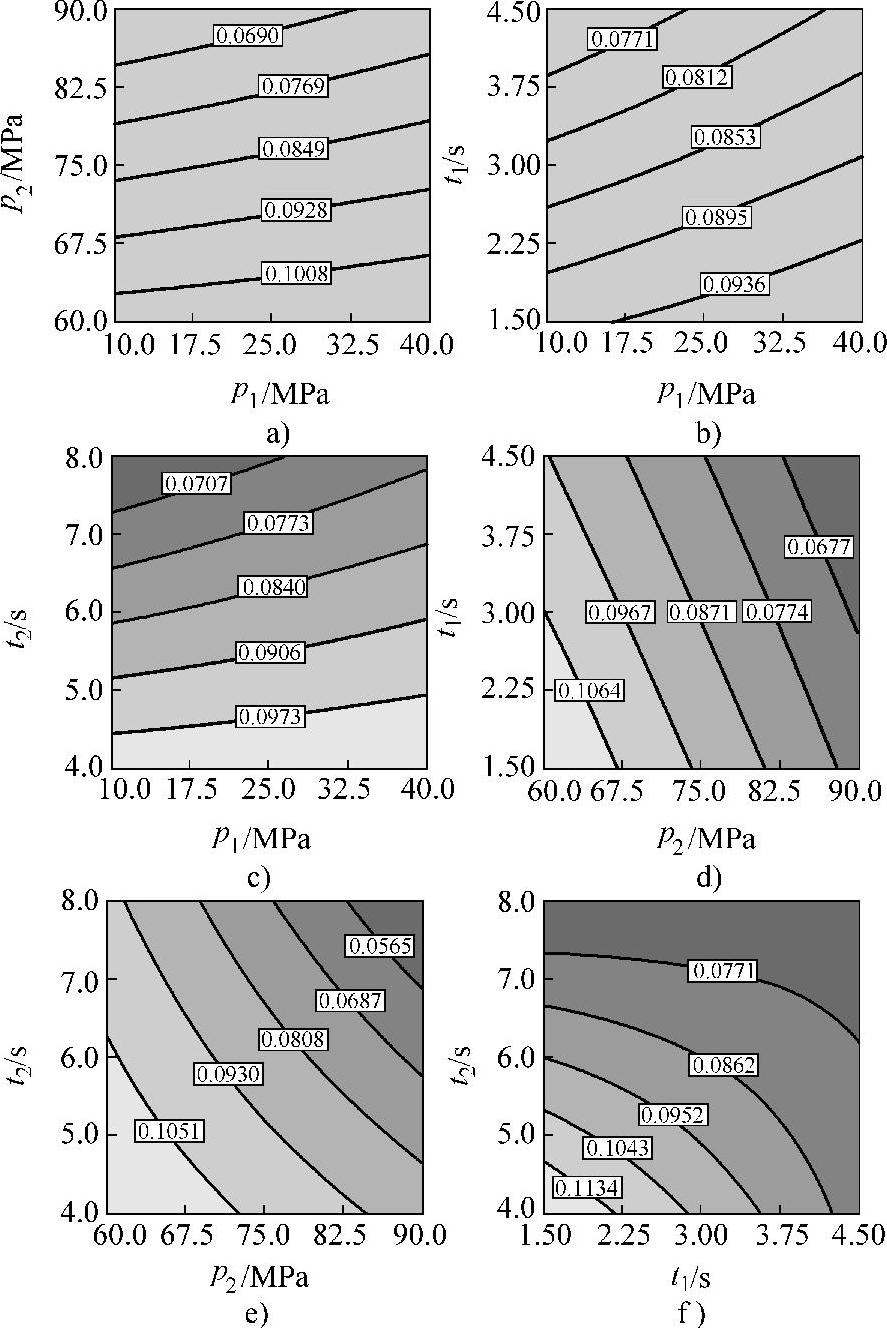
图8-31 模拟获得的多段保压工艺参数对缩痕深度的影响

a）p₁和p₂ b）p₁和t₁ c）p₁和t₂ d）p₂和t₁ e）p₂和t₂ f）t₁和t₂

根据表8-3中的模拟试验数据，利用基于最小二乘法的回归分析，拟合得出了可用于预测塑件Z向最大翘曲变形量和表面最大缩痕深度的多项式数学模型，分别见式（8-2）和式（8-3）。表8-4和表8-5分别为关于塑件最大翘曲变形量和缩痕深度数学模型的变量分析结果。对于翘曲变形，t₁、t₂、p₂t₂、t₁t₂、p²₁、p²2和t²₂为重要项，而对于缩痕深度，p²₁、p²₂、t₁、t2、p1 t1和t1 t2为重要项。式（8-2）与式（8-3）的多项式数学模型为

W_z=27.57888+1.26927p₁-3.62963p₂+21.64306t₁+11.09332t₂+0.0011519p₁p₂+0.0022417p₁t₁-0.012152p₁t₂-0.081758p₂t₁+0.15371p₂t₂-1.71769t₁t₂-0.028867p²₁+0.018930p²₂+0.42620t²₁-0.92643t²₂（8-2）(www.daowen.com)

S=0.22111+0.0022320p₁-0.011606p₂+0.011606t₁-0.020499t_2-0.0011189p₁t₁+0.0044250t₁t₂（8-3）

由上述分析可知，多段保压工艺参数对塑件翘曲变形和缩痕深度的影响比较复杂。为了获得最佳的工艺参数组合，减小塑件的翘曲变形和缩痕深度，需要对多段保压工艺变量进行优化设计。工艺优化设计的目标是在保证塑件翘曲变形不影响后续装配使用的前提下，尽量减小塑件表面的缩痕深度，以获得最优的塑件外观品质。基于上述优化设计策略，可建立如下形式的优化目标模型和约束函数

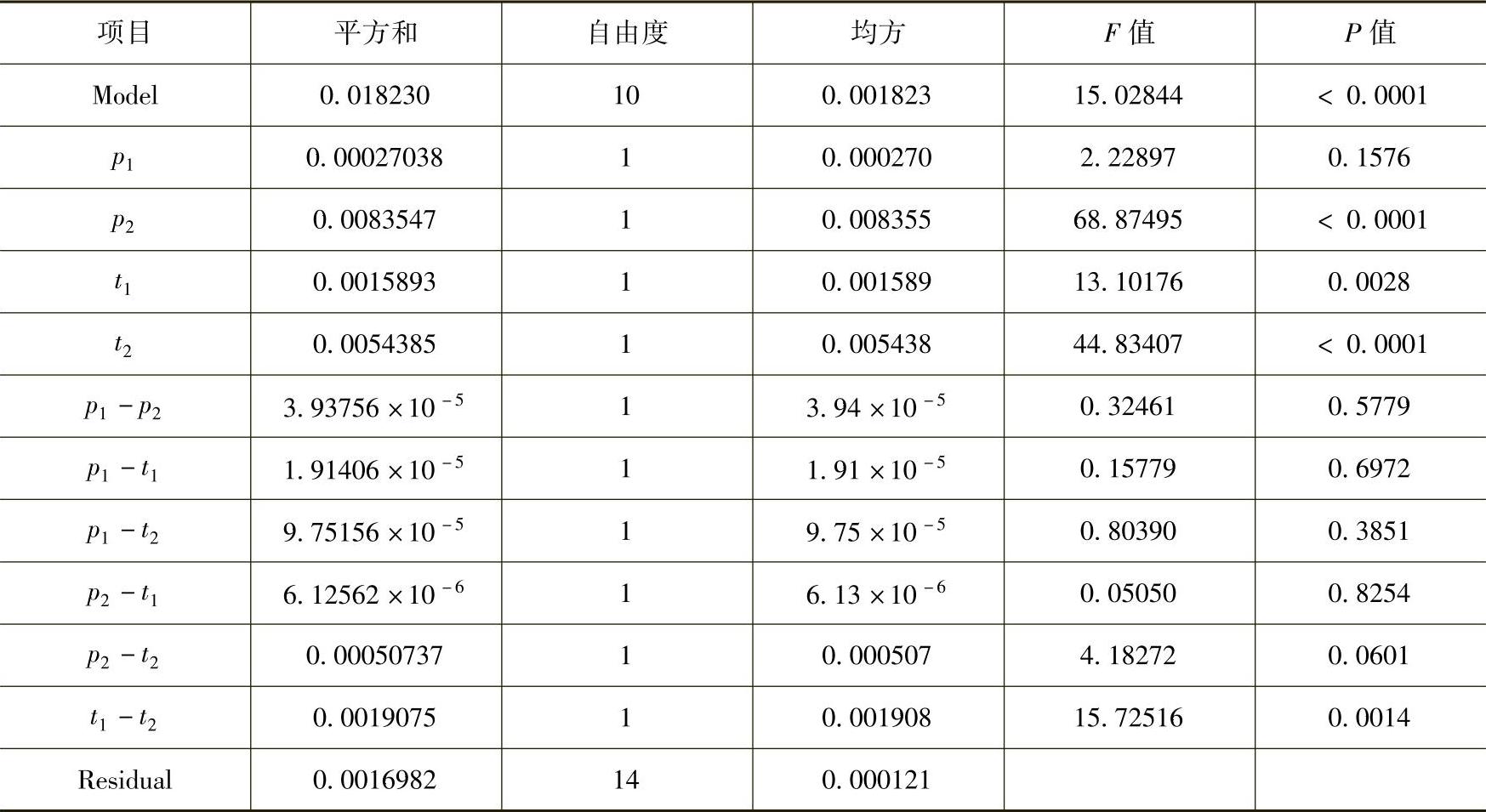
表8⁃4 塑件翘曲变形回归模型的变量分析结果

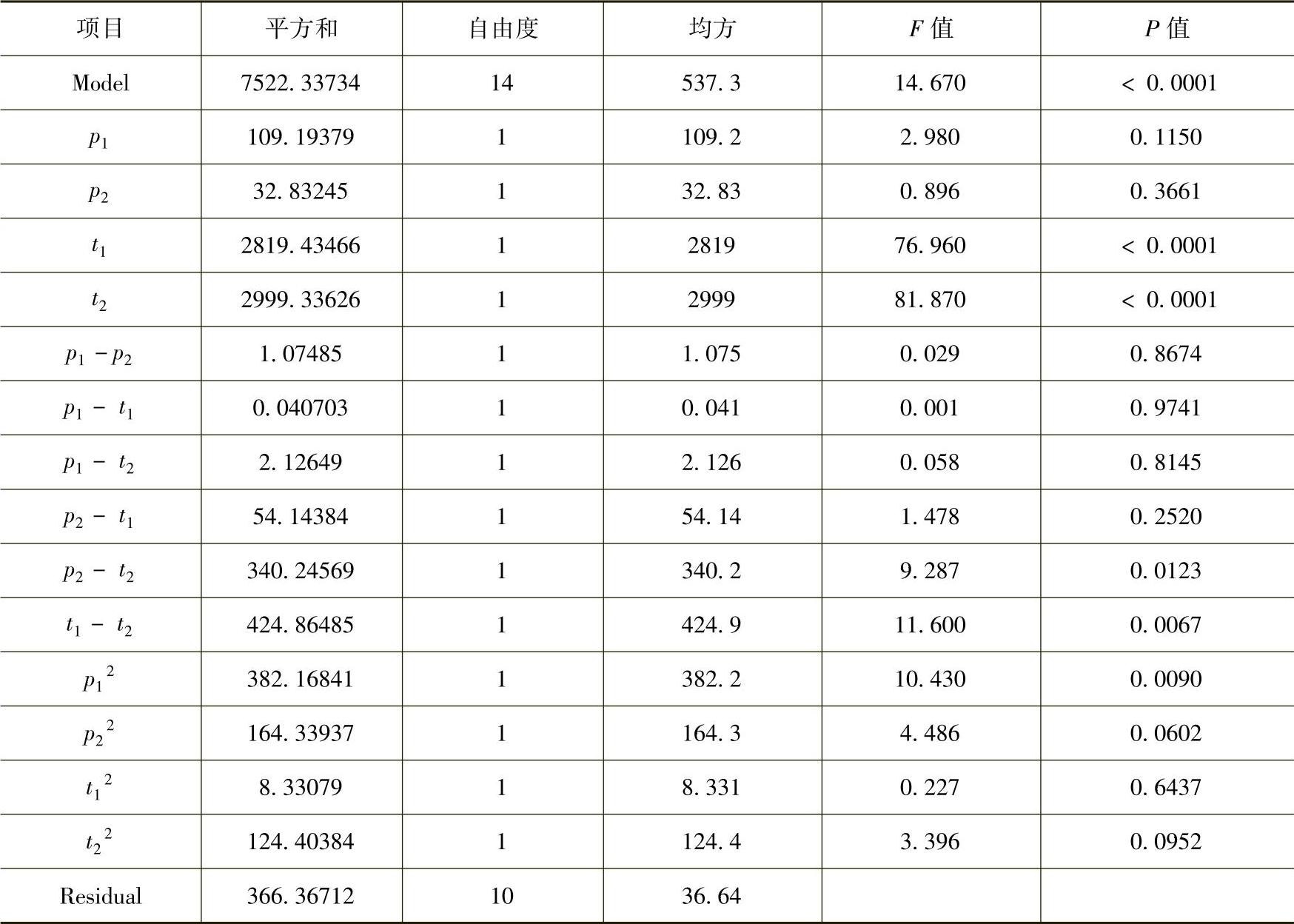
表8⁃5 塑件缩痕深度回归模型的变量分析结果

求解变量：p₁，p₂，t₁，t₂

最小化：S（p₁，p₂，t₁，t₂）

约束条件：

|W_z（p₁，p₂，t1，t2）|≤5.0mm （8-4）

变量取值范围：

10MPa≤p₁≤40MPa，60MPa≤p₂≤90MPa，1.5s≤t₁≤4.5s，4s≤t₂≤8s

利用我们自主开发的多目标优化程序对上述问题执行带约束的非线性优化，优化后获得的最佳工艺变量组合和目标函数值见表8-6。为了验证优化结果的有效性，根据优化后获得的最佳工艺参数组合，再次执行注塑模拟分析，模拟获得的塑件最大翘曲变形量和缩痕深度分别为4.858mm和0.0436mm，优化结果与模拟计算结果之间的相对误差分别为2.92%和-4.36%，均符合工程计算的误差要求。与经优化的单段保压方式相比，经优化的多段保压方式将塑件的翘曲变形量和缩痕深度分别减小了64.7%和73.7%；而与未经优化的保压方式相比，塑件的翘曲变形量和缩痕深度则分别减小了76.3%和75.0%，从而显著提高了液晶电视机面板的形状和尺寸精度及表面质量。

表8⁃6 多段保压工艺的优化设计结果和对应的模拟结果