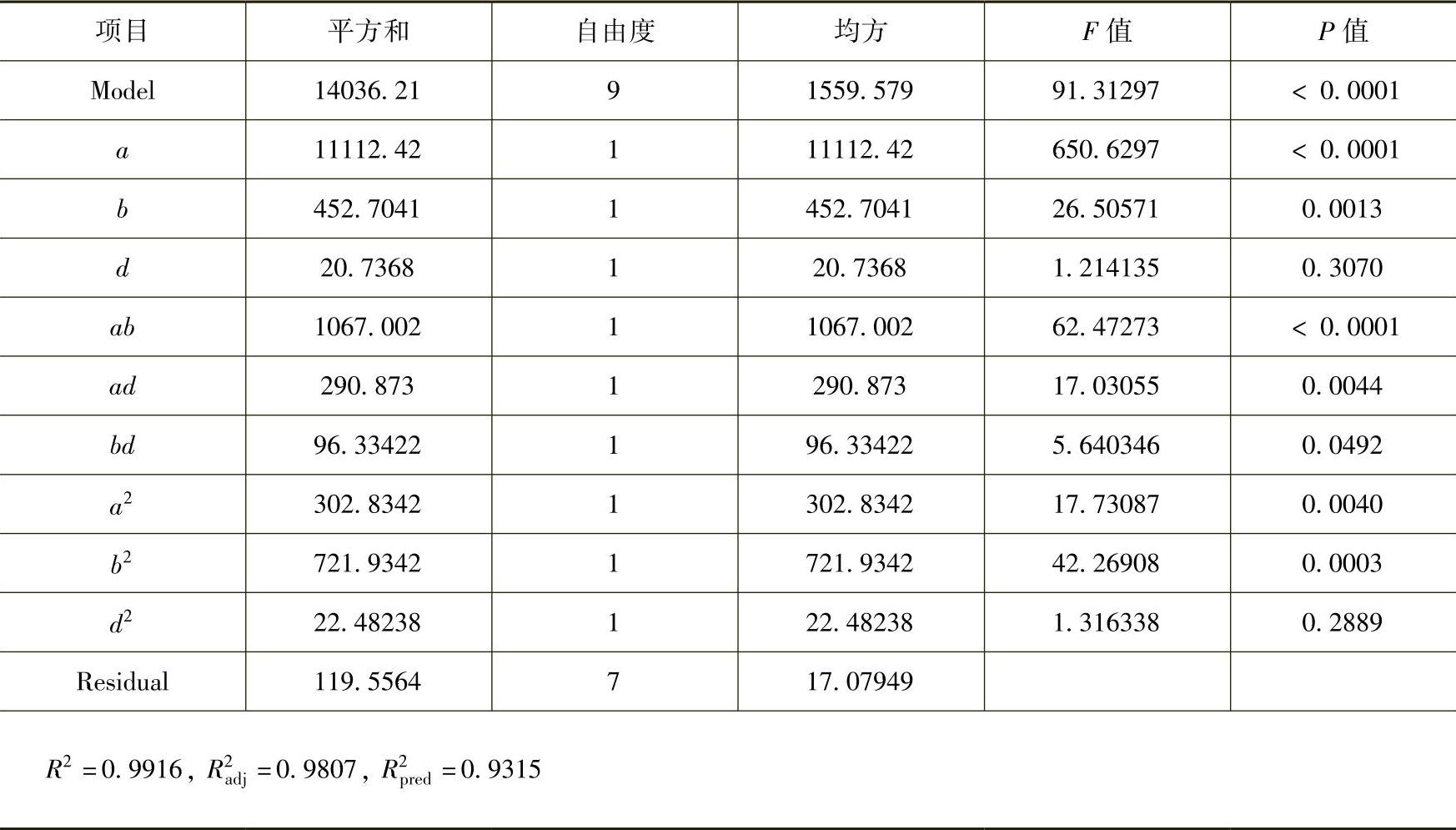
回归拟合的响应曲面模型在统计学上的重要性可以通过ANOVA分析进行评估和检测。表7-3～表7-5分别所示为响应变量t_rh、T_max和σ_max对应的ANOVA分析结果。从表中可以看出，各响应曲面模型的回归可决系数、调整可决系数以及预测可决系数均非常接近1，这表明响应曲面模型具有非常高的拟合精度，可以实现响应变量的精确预测。F检验表明，三个响应曲面模型的F值分别为1227.98、286.63和91.31，均达到0.01的显著水平检验。P检验表明，对于t_rh，所有的一次项（a、b、d）、二次项（a²、b²、d²）和交叉项（ab、ad、bd）的P值均小于0.05，这表明它们均为模型的重要项；对于T_max，一次项（a、b、d）、二次项（b²）和交叉项（ab、ad、bd）为重要项，而二次项（a²、d²）为非重要项；对于σ_max，一次项（a、b）、二次项（a²、b²）和交叉项（ab、ad、bd）为重要项，而一次项（d）和二次项（d²）为非重要项。

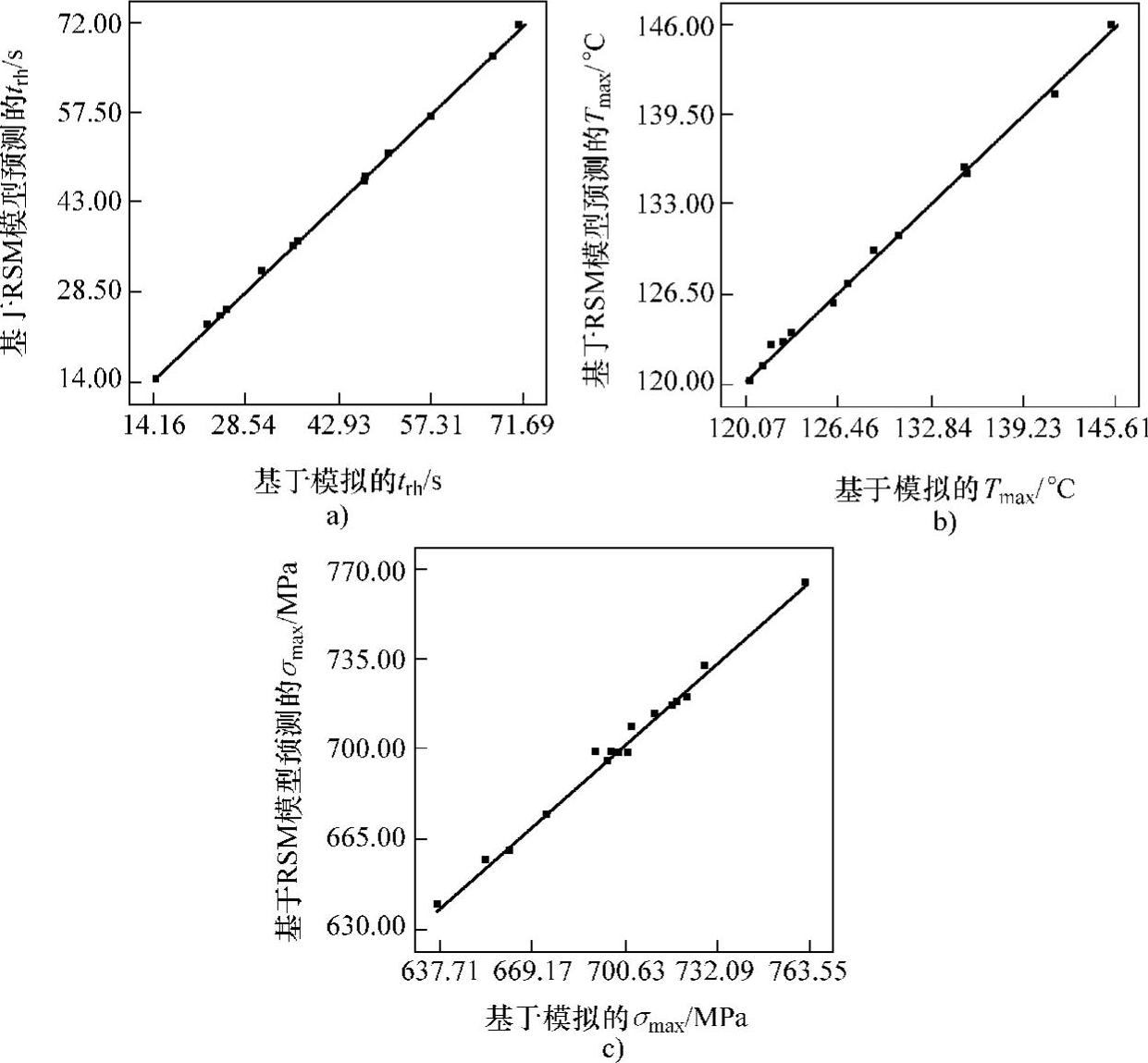
图7-6 响应曲面模型预测值与模拟计算值的对比

a）t_rh b）T_max c）σ_max

表7-3 加热时间t_rh回归模型的变量分析结果

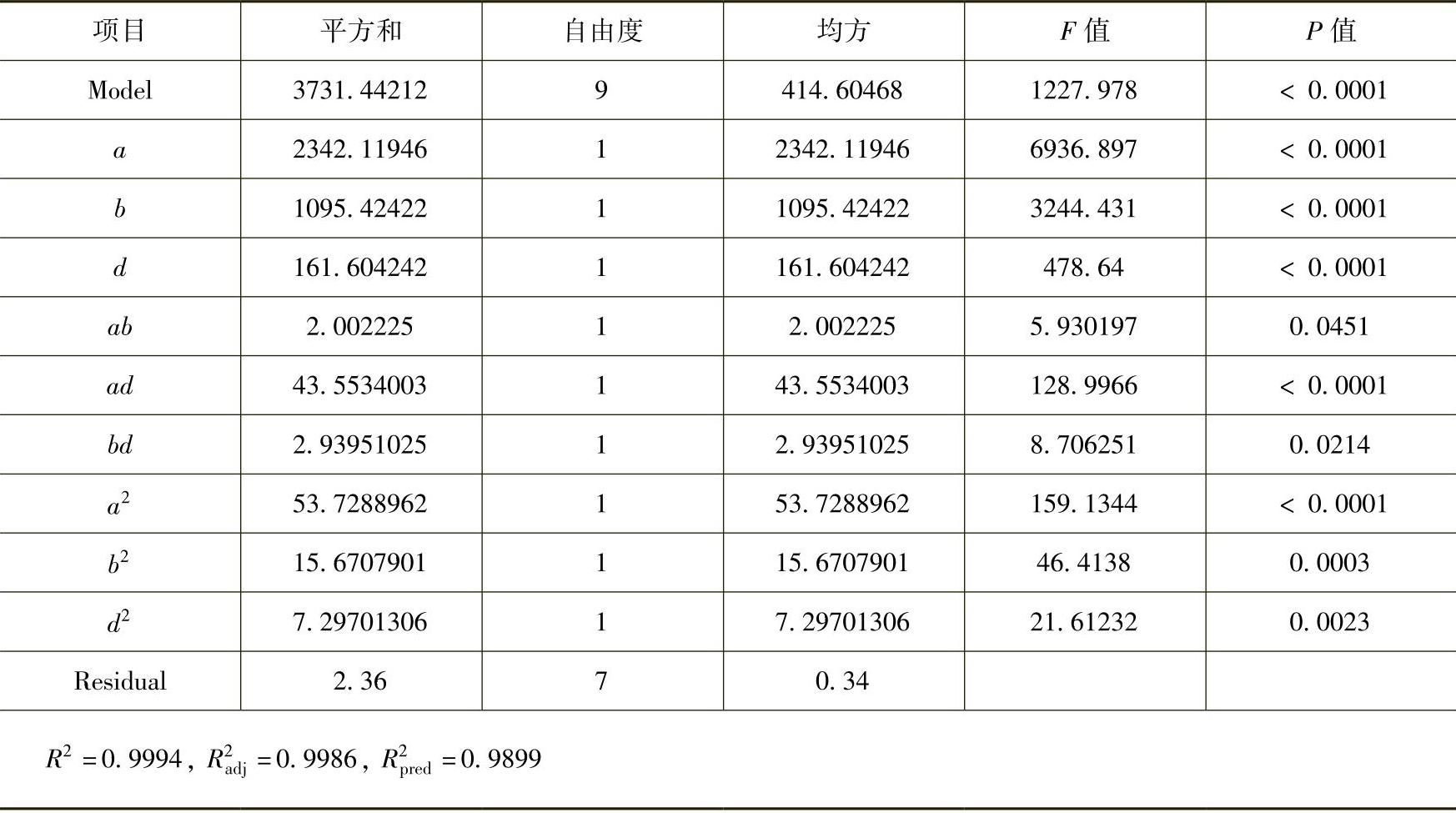
表7-4 最高型腔表面温度T_max回归模型的变量分析结果(www.daowen.com)

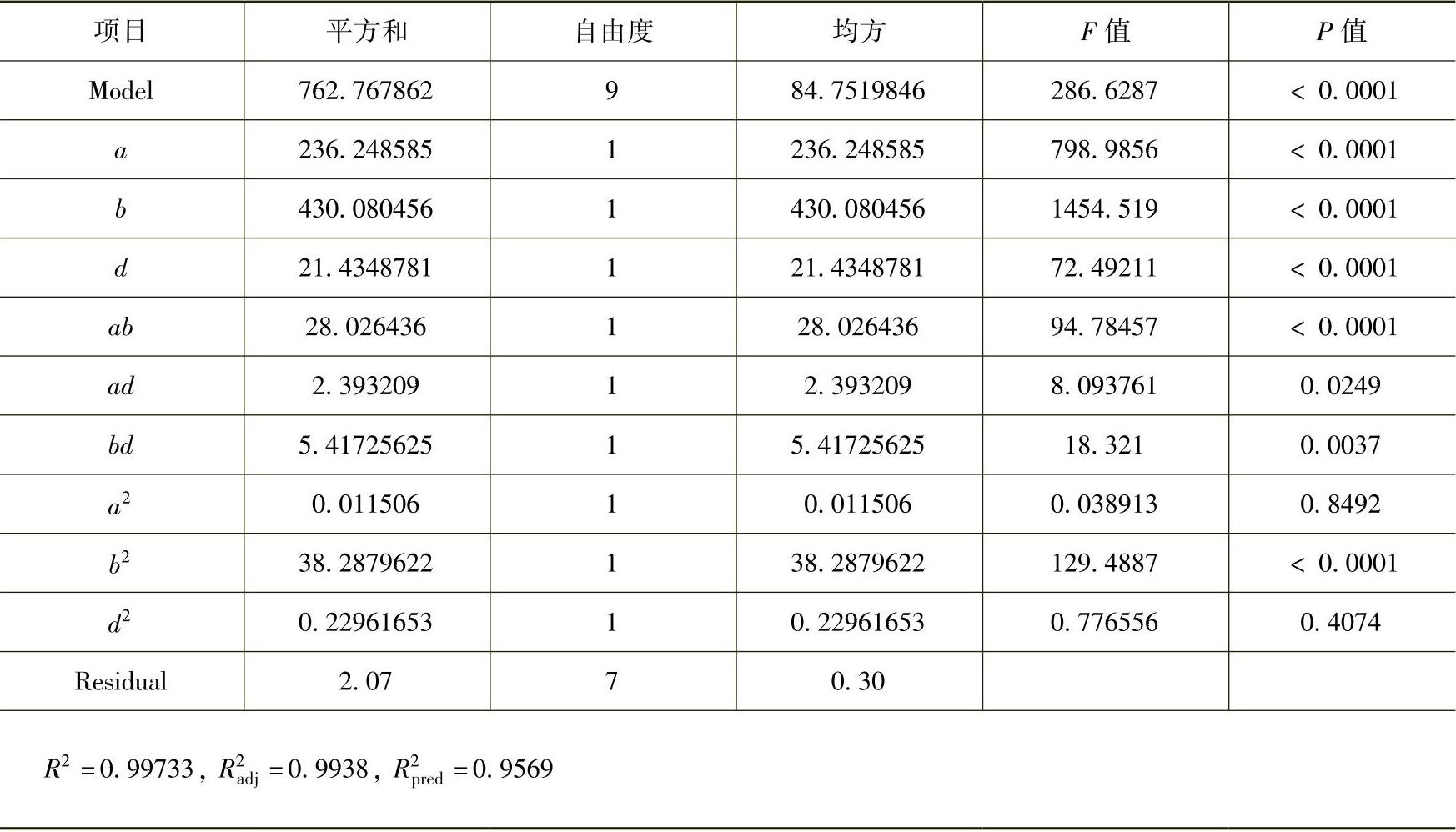
表7-5 最大热应力σ_max回归模型的变量分析结果

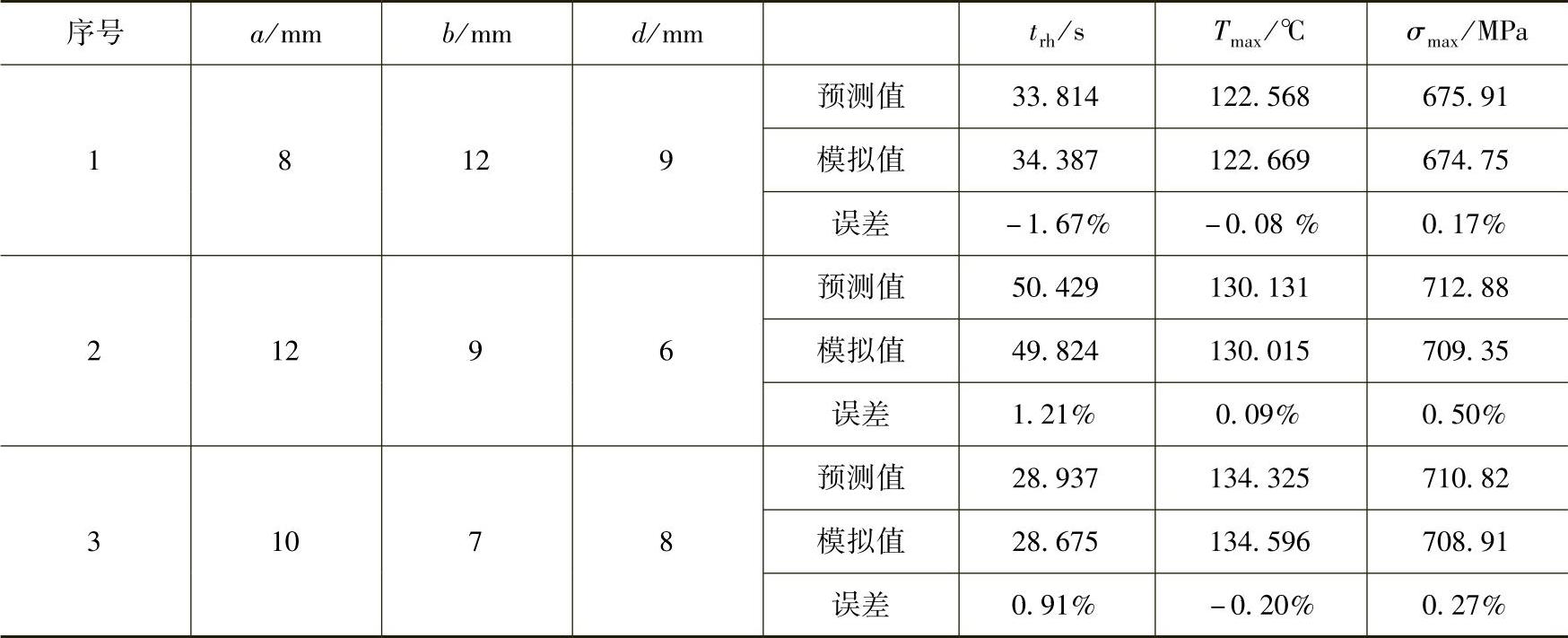
在设计空间范围内任意取三组未包含在表7-2中的设计变量组合，分别利用拟合的响应曲面模型和有限元模拟方法计算各设计变量组合对应的响应变量值，通过对比分析，以进一步验证响应曲面多项式模型的有效性。表7-6列出了对比分析结果。从表中的数据可以看出，三个响应曲面模型预测值的最大误差的绝对值分别为1.67%、0.20%和0.50%，均在工程计算允许的误差范围内，这表明拟合的响应曲面模型具有比较高的预测精度，可以用于响应变量值的预测和评估。

表7-6 基于响应曲面多项式模型和有限元模拟的计算结果对比