根据表7-2中的试验数据，结合式（7-3）可回归拟合出设计变量与响应变量之间的二次响应曲面模型。式（7-14）～式（7-16）分别所示为三个响应变量对应的响应曲面模型的数学表达式，即

t_rh=0.87543+2.66991a+0.92897b-2.31680d+0.044219ab-0.41247ad-

0.10716bd+0.22326a²+0.12057b²+0.32911d²（7-14）

T_max=127.79129+2.17409a-2.78431b+0.37215d-0.16544ab+0.096687ad-

0.14547bd+0.00326719a²+0.18847b²+0.058381d²（7-15）

σ_max=555.86950+21.59875a-3.13312b+3.91300d-1.02078ab+1.06594ad-(www.daowen.com)

0.61344bd-0.53005a²+0.81839b²-0.57769d²（7-16）

与时间成本较高并且过程相对复杂的有限元模拟计算相比，上述拟合得出的响应曲面模型为响应变量的计算提供了一种更为简便和高效的方法。但在利用这些响应曲面模型计算响应变量之前，首先应当对它们的准确性进行检验。利用残差分析可以对响应曲面模型的准确性进行诊断。图7-5所示为三个响应曲面模型对应的残差正态概率分布。从图中可以看出，每一个响应变量对应的残差均沿一直线分布，这表明响应曲面模型的预测误差呈正态分布，验证了最小二乘法的拟合精度是足够的。图7-6所示为利用响应曲面模型预测的响应变量值与模拟试验获得的响应变量值之间的对比。从图中可以看出，响应曲面模型的预测结果与模拟试验结果具有很好的一致性，这表明在给定的设计空间里响应曲面模型具有较高的预测精度。

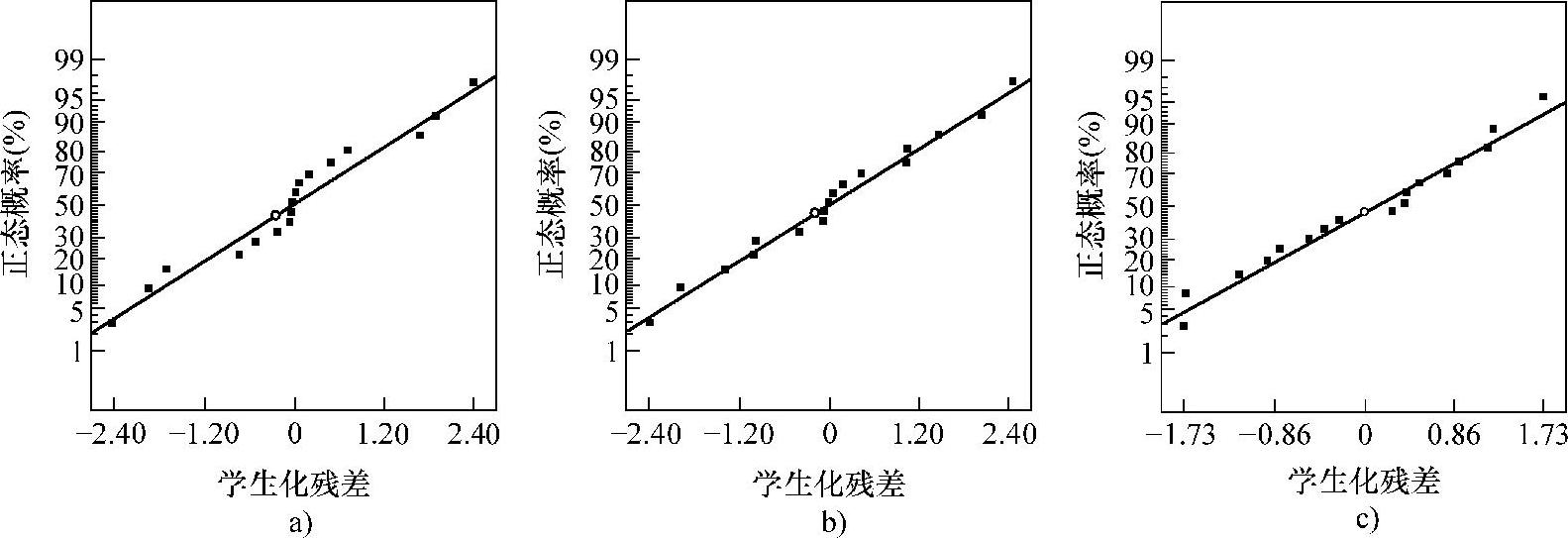
图7-5 三个响应曲面模型对应的残差正态概率分布

a）t_rh b）T_max c）σ_max