响应曲面法（Response Surface Methodology，简称RSM）是一种结合统计分析和数学应用的试验设计方法，用于探寻和评价设计变量（又称输入变量、过程变量、影响因子或影响因素）与响应变量（又称目标变量或解释变量）之间的数学模型关系。设计变量与响应变量之间的真实函数关系可用下面的模型表示

Y=f（x₁，x₂，···，x_n）+ε（7-1）式中，Y表示响应变量；f表示设计变量与响应变量之间的未知真实函数；x表示设计变量；n表示设计变量的个数；ε表示随机误差，代表测量误差、背景噪声以及函数f中未包含的其他变量等因素的影响。

在RSM的实际应用中，需要为真实响应曲面或函数f建立一个近似的数学模型，最常用的近似数学模型为一阶或二阶泰勒多项式。为了可以更加精确地预测响应变量，可以采用二阶泰勒多项式拟合响应曲面模型，其数学表达式为

式中，β₀表示模型常量；β_i表示线性项系数；β_ii表示二次项系数；β_ij表示交叉项系数。

基于式（7-2）的二次多项式模型，设计变量组合与响应变量之间的对应关系可用下面的矩阵方程式表示

Y=Xβ+ε（7-3）

式中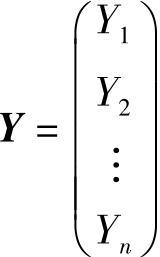，表示响应变量的数值集合；表示设计变量组合的(www.daowen.com)

数值矩阵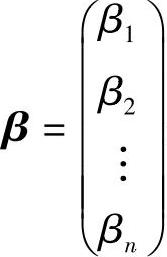；表示多项式模型中的未知系数；表示残差向量。未知系数向量β可通过基于最小二乘法的回归分析估计，其通用的数学表达式为

β=（X^TX）^-1X^TY （7-4）

式中，X^T表示矩阵X的转置矩阵；（X^TX）^-1表示矩阵X^TX的逆矩阵。

值得注意的是，为了避免矩阵X^TX的奇异性，试验样本数据的组数应当多于未知系数的数量。

在RSM中，回归分析所需的样本数据是通过专门的试验设计获得的。在标准的RSM中，最常用的试验设计方法主要有Box-Behnken设计（Box-Behnken Design，简称BBD）和中心复合设计（Central Composites Design，简称CCD）两种形式。在试验设计中，不同水平的设计变量组合对应的响应变量的值可以通过真实试验或者数值模拟计算获得。