在除尘工程中，含尘气体是以风机为动力通过风管而输送的。风管设计和风机选择都会影响整个除尘系统的效果。而风管设计和风机选择都涉及一些流体力学基本概念，如空气在风管中流动时的能量变化、压力损失等。

气体在风管中流动时，除高温气体外，压力和温度一般不会有很大的变化，不致引起空气密度的显著变化，故可称为定容运动。气流在风管中流动时，有两种不同的压力：动压和静压。

1.动压

动压是流动空气的动能，与空气流速直接有关，永远是正值。动压的表示式如下，即

p_d=ρv²/2 （8-5）

式中 p_d——动压指单位体积气体的运动能量（Pa）；

v——气体运动的流速（m/s）；

ρ——气体的密度（kg/m³）。

2.静压

静压是单位体积空气作用于周围物体的压强，简称静压，与空气的流动无关，静压值通常相对于大气压力而言，又称相对静压。把大气压力作为基点，大于大气压力时就为正值，反之为负值。

3.全压

动压和静压的代数和称为全压，代表气体在风道中流动时的全压力，即

p_T=p_d+p_s=ρv²/2+p_s （8-6）

式中 p_T——全压（Pa）；

p_s——静压（Pa）。

4.气体在管道中流动时的能量变化

空气在风管内作定容运动时的能量变化，通常用伯努利方程式来表示。

对于风管内的两个截面（截面1和2）来说，伯努利方程式为

式中 p_s1、p_s2——位于截面1和截面2处的单位体积空气的压力能，即静压（Pa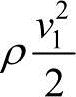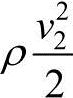）；、——位于截面1和截面2处的单位体积空气的动能，即动压（Pa）；

Δp——在截面1和截面2之间的单位体积空气的能量损失，即压力损失（Pa）。

由上式可见，方程式表达了风管内空气的流速和压力之间的关系。Δp表示全压的损失，它用于克服风道内的局部阻力和摩擦阻力。

若截面1和截面2的截面积分别为A₁和A₂。当风管的截面积不变时，即A₁=A₂，则v₁=v₂，由上式公式Δp=p_s1−p_s2。这就是说，空气流经截面积不变的风道截面1至截面2的能量损失等于两处的静压差。

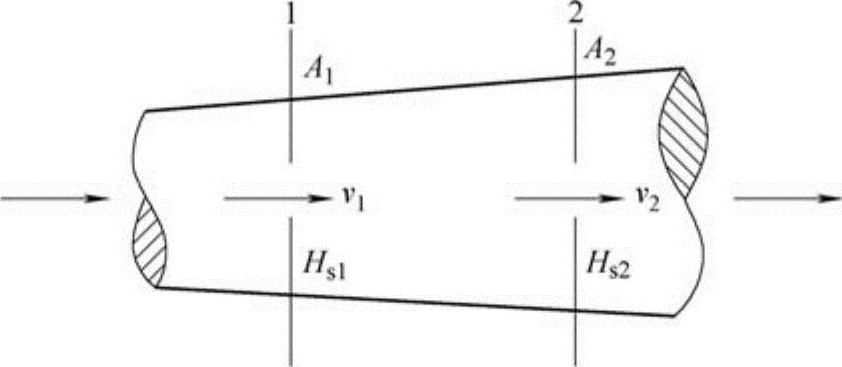
图8-3 变径管能量转化示意

因风管内各个截面上的总能量是不变的，故动能和位能可以互相转化，也就是动压和静压是可以互相转化的。如图8-3所示，当截面1和截面2的截面积不相同时，即A₁<A₂，由于通过风管的空气流量不变，所以v₁>v₂，因此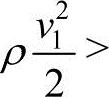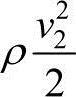，即截面1的动压大于截面2的动压。因总能量不变，由上式可知，截面1的静压必然小于截面2的静压。由此可见，空气由截面1流到截面2时，动压变小，静压变大。

5.流动状态(www.daowen.com)

风管中空气的流动状态可以分为层流和紊流两种。

1）层流：是各股流体形成互相平行的流速，呈有秩序地流动，不相混淆，也不产生涡流。

2）紊流：是气流在风管的横截面上发生脉动，毫无秩序地紊乱流动形成涡流。由层流运动过渡到紊流运动是在一定的惯性力和流体内摩擦力的相互关系下发生的。

3）雷诺数：标志空气在风管内的流动状态的准数称为雷诺数。雷诺数用下式表示，即

式中 R_e——雷诺数；

D——管道直径（m）；

v——气流速度（m/s）；

ν——气体的运动黏度（m²/s）；

μ——流体的动力黏度（Pa·s）；

ρ——气体密度（kg/m³）。

气体的动力黏度和运动黏度，随着气体温度的升高而增长。气体压力增高时，动力黏度增大，而运动黏度减小。当压力小于1MPa时，对气体的动力黏度的影响可以忽略不计。

实验证明，流体在直管内流动时，当雷诺数R_e≤2000时，流体黏滞力超过流体的惯性力，流体的流动类型属于层流，当R_e≥4000时，流体的惯性力超过流体黏滞力，产生紊流运动，流体的类型属于紊流；而R_e值在2000～4000的范围内，可能是层流，也可能是紊流，若受外界条件的影响，如管道直径或方向的改变，外来的轻微振动，都易促成紊流的发生，所以将这一范围称为不稳定的过渡区。在生产操作条件下，常将R_e>3000的情况按紊流考虑。

由层流转变为紊流时的雷若数值，称为临界值，常数R_e=2320。当雷诺数到达临界值时，相应的气体流速称为临界速度。

6.压力分布

空气在管道内流动时，由于除尘管道的阻力和流速等的变化，除尘管道中空气的压力也随之发生变化。了解管道内压力的变化规律，对通风系统的设计和运行管理都很重要。下面我们根据流体力学原理，分析管道内的压力分布规律。

（1）简单系统中的压力分布

图8-4所示为一简单除尘管道系统，在风机前为一简单管段，风机后为一断面较小的直管段，风机的入口及出口均设有格栅。

（2）复杂管网系统中压力的分布

图8-5所示为复杂风管系统中空气压力的分布示意图。该系统内有局部排气罩、除尘器、风机、排气风帽等设备。

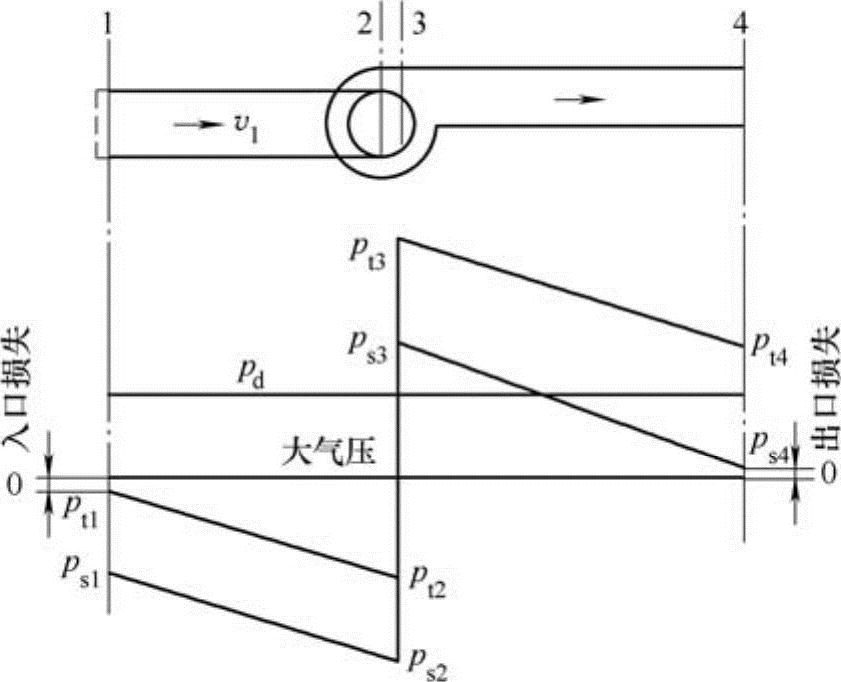
图8-4 简单风管系统的压力分布

图8-5 复杂风管系统的压力分布

1—砂轮 2—袋式除尘器 3—排气风帽 4—风机