头型的不同会直接影响流动的分离点发生改变，进而对航行体的空化水动力特性产生影响，如图6-35所示。因此设计者有必要对水下航行体的非定常空化流动有更清楚的认识和把握，以便为水下航行体头部外形的设计提供一定的理论基础。

图6-35　水下航行体外形示意图

（a）潜射导弹；（b）鱼雷

6.3.1.1　头型对初生空化流动特性的影响分析

空化的发生和流场结构之间存在重要的关系，并且初生空化流场对后续空化现象的发展有着重要的影响。为了研究初生空化的流场特性，本节采用数值模拟与实验研究相结合的方法对绕不同头型回转体的初生空化流场结构进行了分析。

图6-36分别给出了采用计算和实验得到的不同头型的回转体初生空泡形态，计算中，空泡用含汽量为0.8（αv=0.8）的等值面表示。从图中可以看出，对于不同头型，所对应的初生空化数各不相同，在目前的实验工况下，平头回转体的初生空化数为1.20，锥头回转体的初生空化数为0.95，半球型回转体的空化数远小于其余两种头型回转体，其初生空化数为0.65左右。头型对初生空化流场结构会产生较大的影响：对于平头回转体，如图6-36（a）所示，由于其肩部的曲率突变，高剪切流动区在此处形成明显的涡旋结构，在涡心处压力降低到液体的汽化压力时就会有空化现象的产生，故绕平头回转体的初生属于旋涡空化；对于锥头回转体，其肩部的曲率也会也有明显突变，初生空化也属于脱体涡空化。对比上述两种头型的回转体，在很大程度上，半球型的空泡脱体属于自然分离。当空化数为0.65左右时，在半球型回转体前端会形成薄薄的初生片空泡，附着空泡呈现明显的“指状”分布。由图6-36（c）的流线图可以看出，此时空化流场结构比较稳定，在回转体肩部无明显的旋涡结构。

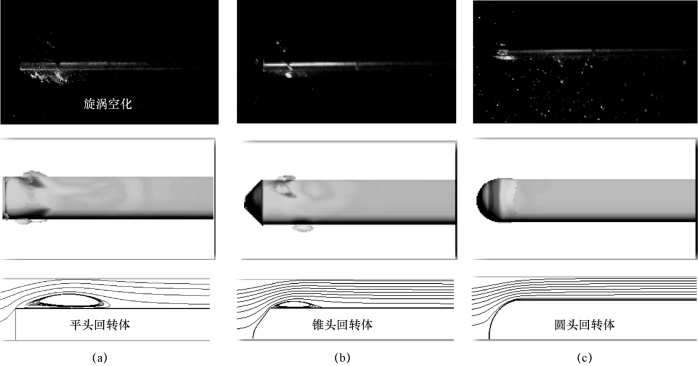
图6-36　绕不同头型回转体的初生空泡形态及流场结构

（a）平头回转体σ=1.20；（b）锥头回转体σ=0.95；（c）圆头回转体σ=0.65

图6-37分别给出了在初生空化数下，不同头型回转体表面的压力系数分布情况。不同头型的回转体表面的压力系数均呈现出以下的分布规律：由驻点最大值急剧下降，当到达斜面分离涡区时，压力系数下降到负压最大值而逐渐区域稳定，接着压力系数逐渐上升，而后达到一个稳定区域。头型对回转体肩部的压力分布趋势也有着非常重要的影响，由于在平头回转体的肩部存在明显大尺度的旋涡结构，所以该头型得到的低压区域要明显大于其他两种头型，半球型回转体肩部的低压区域最小。

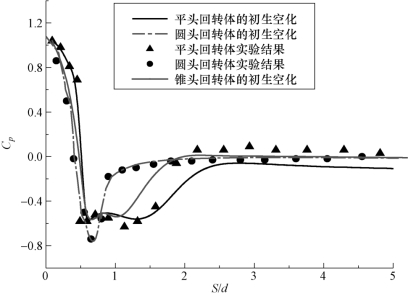
图6-37　不同头型回转体表面的压力系数分布

为了更为详细地了解头型对回转体空化现象的影响，图6-38给出了不同头型回转体，其肩部分离点位置的差异。对于平头回转体，数值模拟所预测的流动再附着点的位置与Katz（1984）实验结果较为吻合，进一步验证了研究中所采用数学模型的正确型。平头回转体得到的回流区可达距头部2.5d处（d为回转体直径），而锥头回转体得到的回流区明显小于平头回转体，仅可达距头部1.5 d处。对于分离特性较小的半球型回转体，在初生工况下，并没有回流的产生。

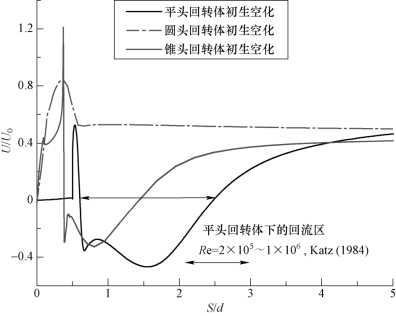
图6-38　不同头型回转体表面再附着区域

图6-39分别相应给出了在初生空化工况下，数值计算得到的不同头型回转体周围的湍流动能k及湍流耗散ε的分布情况，k和ε是表征流场中的脉动特性的重要物理参量，在k和ε较大的区域，说明该区域内的速度以及动量交换比较频繁，湍流脉动比较剧烈。由图6-39可以看出，不同头型回转体周围的湍流脉动特性有明显的差异，在平头回转体壁面附近的剪切层中，湍流动能、湍流耗散率及其影响范围明显大于其他两种头型的回转体。说明在平头回转体壁面附近的剪切层附近，体现出更为明显的旋涡脉动特性。相较而言，圆头回转体周围则基本没有高湍动能及湍流耗散区域，说明此处流动比较稳定，无明显的旋涡脉动区域。

图6-39　绕不同头型回转体湍流动能和湍流耗散率k和ε的分布（见彩插）

（a）湍流动能分布；（b）湍流耗散率分布

6.3.1.2　头型对片状空化流动特性的影响分析

图6-40分别给出了平头回转体和锥头回转体在3种不同空化数下的典型形态对比。可以发现，空化数为0.8时，两种回转体的空穴已基本均匀包裹着回转体肩部的整个圆周，呈现为片状空化。对于平头回转体而言，空穴形态呈现为游离状的小尺度空泡团的聚集状，其表面并不光滑。相比之下，锥头回转体的空穴表面比较光滑且靠近肩部的部分空穴已呈现附着层状。随着空化数的降低，空化得以进一步的发展，两种回转体的空穴尺度均逐渐增大，且空穴界面逐渐变得光滑清晰，呈椭球状包裹回转体的头部，片状空化逐渐转变为云状空化。与锥头回转体相比，平头回转体的云状空化程度更加剧烈。

图6-40　两种回转体在不同空化数下的典型空穴形态图

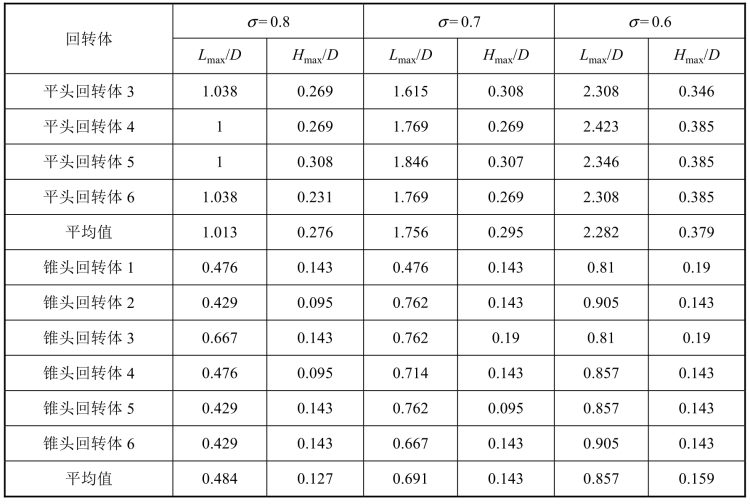
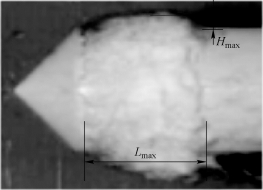
为了对比随着空化数的变化，两种回转体的空穴发展特性，表6-4分别列出了两种回转体在不同空化数下，6个不同发展周期内的最大空穴尺度值。其中，统计量为最大空穴的长度Lmax及厚度Hmax，两种尺度的定义如图6-41所示。由表6-4的数据可知，即使在相同的工况下，不同周期的空穴发展情况也有所不同，为了更形象地对两种回转体最大空穴长度和厚度进行比较，图6-42（a）～（c）分别给出了与表6-4统计数据对应的曲线图，其中蓝色曲线表示空穴厚度，黑色曲线表示空穴长度。从图中可以看出，相同空化数下，无论是空穴的长度还是厚度，平头回转体均要大于锥头回转体的。对比不同空化数下的曲线变化可知，随着空化数的减小，曲线的波动亦逐渐减小，即不同周期间的最大空穴尺度的差异逐渐减小，从而说明空化数较小时，空穴的周期性发展更加明显。

表6-4　各工况下，最大空穴的长度及厚度统计

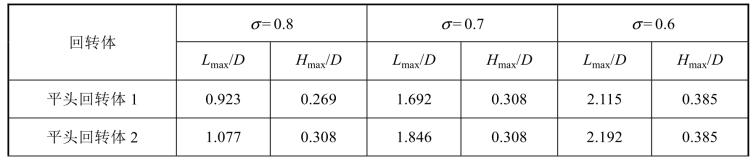
续表

(www.daowen.com)

图6-41　最大空穴长度及厚度的示意图

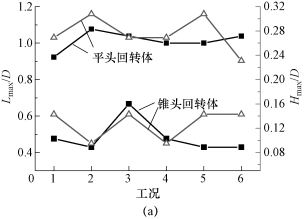
图6-42　不同头型回转体在不同空化数条件下的最大空穴尺度对比（见彩插）

（a）σ=0.8

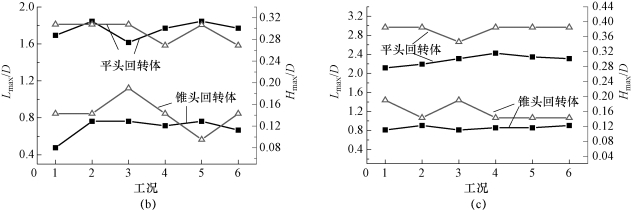
图6-42　不同头型回转体在不同空化数条件下的最大空穴尺度对比（续）（见彩插）

（b）σ=0.7；（c）σ=0.6

为了进一步分析头型对片状及云状空化流动特性的影响，图6-43分别给出了不同空化数下平头回转体和锥头回转体的时均速度u的分布云图。从图中可以看出，随着空化数的减小，与空穴对应的低速区域逐渐增大，分离区域也逐渐外扩。相比于平头回转体，相同空化数下，由于锥头回转体肩部的空穴尺度较小，其对应的低速区域亦远小于平头回转体。

图6-43　不同头型回转体片状和云状空化阶段时均速度u的分布云图（见彩插）

（a）平头σ=0.8；（b）锥头σ=0.8；（c）平头σ=0.7；
（d）锥头σ=0.7；（e）平头σ=0.6；（f）锥头σ=0.6

为了更直观地了解片状和云状空化区域内速度的分布情况，图6-44给出了两种回转体在不同空化数下，时均空泡厚度的中心水平剖线上的时均速度u的分布曲线，剖线的起始点为回转体的肩部。由图6-44可知，随着空化数的减小，两种回转体空穴内的时均速度u沿轴向方向的分布趋于均匀、速度梯度减小，并且由于空穴的不断发展，其沿轴向的增长促使空穴内速度u值总体增大。与锥头回转体相比，平头回转体的时均速度曲线随着空化数的变化更为复杂，当空化数为0.8时，时均速度曲线呈现W形或波浪状，已完全改变了原时均流场的结构。另外，仔细对比两种回转体的速度曲线随空化数的变化可以发现，平头回转体空穴内速度的总体增长幅度较大，这便说明随着空化数的降低，平头回转体空穴的增长速度较大。

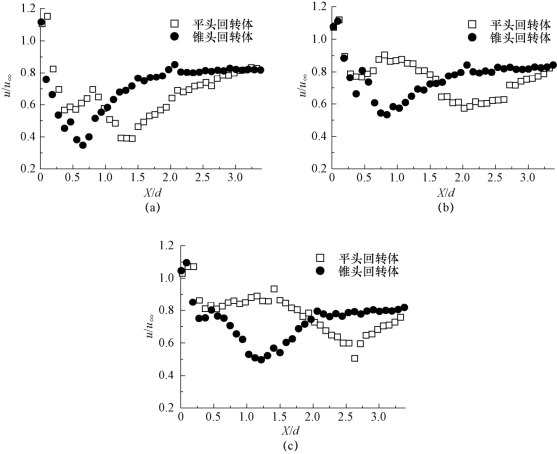
图6-44　不同空化数下，两种回转体的时均速度u在特征剖线上的分布情况

（a）σ=0.8；（b）σ=0.7；（c）σ=0.6

6.3.1.3　绕不同头型三维回转体空化流场结构分析

在6.3.1.2节中，主要讨论了头型对于初生和片状空化流场的影响，随着空化数的降低，绕回转体的空化流动呈现不同的阶段性特征。下面，将重点对于在不同空化阶段，非定常空化流场结构进行分析。图6-45首先给出了在空化数分别为0.3时，绕平头型和半球型轴对称体肩部的汽相体积分数云图和轴对称体表面的压力分布计算结果与Rouse和McNown实验结果的对比，图中横坐标为模型表面位置的无量纲化参量（其S表示从前驻点开始沿轴对称体表面到取值点的弧长，d表示轴对称体的直径），纵坐标为压力系数。不同头型回转体表面的压力系数呈现出以下的分布规律：由驻点最大值急剧下降，当到达斜面分离涡区时，压力系数下降到负压最大值而逐渐趋于稳定，接着压力系数逐渐上升，而后达到一个稳定区域。总体而言，计算结果与实验值比较吻合，实验与数值计算结果有较好的一致性。

图6-45　绕三维回转体的空穴形态及表面压力分布

（a）圆头回转体；（b）平头回转体；（c）锥头回转体

图6-46、图6-47和图6-48采用实验与数值模拟相结合的手段描述了在不同空化阶段的典型空穴形态。对于半球型轴对称体，在目前实验工况下，其初生空化数为0.65左右，在回转体前端会形成薄薄的初生片空泡；当空化数降低到0.50左右时，片空泡逐渐拉长，附着空泡呈现明显的“指状”分布，在空泡的继续发展过程中，空泡表面变得光滑，并沿周向覆盖这个模型。此时，附着在弹体头部的空泡明显分为两个区域：一部分为透明状的高含汽区域；另一部分为不稳定的雾状水汽混合脉动区域，空泡界面有明显的不规则扰动现象。在空泡的末端可以发现强烈的随机高频脱落现象，雾状空泡团的频繁扰动和小尺度的空泡云脱落有直接的关系。

图6-46　不同空化数下，绕圆头回转体的空穴形态

（a）实验结果；（b）数值计算结果

图6-47　不同空化数下，绕锥头回转体的空穴形态

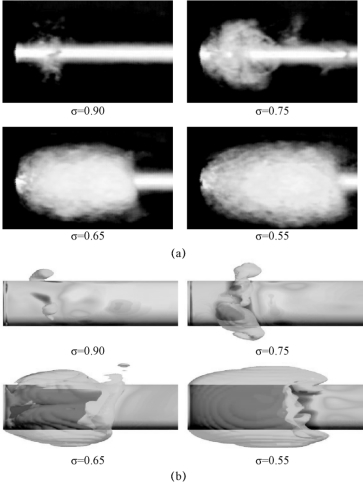
图6-48　不同空化数下，绕平头回转体的空穴形态

（a）实验结果；（b）数值计算结果

回转体头部形状对与空穴形态与空化流场结构有着较大的影响。对于锥头回转体，由于相较半球型，其肩部的曲率存在一定程度的变化。因此，空化初生发生的位置不再附着在回转体上，由于流动在回转体肩部的分离而形成空泡脱体。随着空化数的下降，空穴面积逐渐增大，空泡脱体点的位置有向头部前移的趋势。当空化数为0.50时，绕弹体空化流场处于比较明显的云状空化阶段，在弹体肩部，产生一个椭球形的空化区域，内部为雾状的水-汽混合相，尾部环状气泡在旋涡的作用下上下抖动，存在小范围的空泡脱落现象。随着空化数进一步降至0.30，此时椭球形空化区域达到最大，一直延伸到弹体后部，空泡的长度和形状比较稳定，几乎观察不到空泡的断裂脱落现象。随着空化数的变化，空穴经历了一个稳定-波动-稳定的过程。由于平头与半球型轴对称体的边界层流动特征有很大的差异，因此空穴形态也必然有很大的区别。对于平头轴对称体，由于肩部的曲率突变，致使流动在此强烈分离而形成空泡脱体，其初生空化的本质为涡空化。在很大程度上，半球型的空泡脱体属于自然分离，而平头轴对称体的流动则属于强分离，空泡流动具有明显的涡流特性。半球型轴对称体的初生空化数远小于平头轴对称体的初生空化数。当空化数为0.90时，在平头轴对称体肩部的分离区域内，会首先产生连续的空化涡团结构，空化涡的形成和溃灭逐渐随时间呈现出一定的规律性，但是整个空化区域的边界还不是很明显。随着空化数的降低，空泡区域逐渐变大，形成椭球状的水汽混合空泡团。