结构在水动力作用下的动力学方程定义为

当仅考虑水翼结构在外部激振力和流体作用力的共同作用下绕弹性轴发生振动时，假设水翼结构受到幅值为M0、频率为ωe的外部激振力矩和流体对结构的作用力拒Mfluid，水翼结构单自由度模型如图6-16所示。

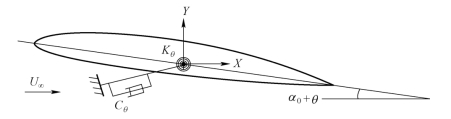
图6-16　水翼结构单自由度模型示意图

式（6.1）可以简化为

Theodorsen模型和Munch模型可以对流体作用力进行预测，其中Theodorsen模型基于不可压缩、无黏流动，流体对结构的作用力矩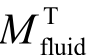表述为

Theodorsen函数C（k）是折合频率的复函数，如图6-17所示，表述为

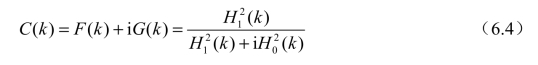
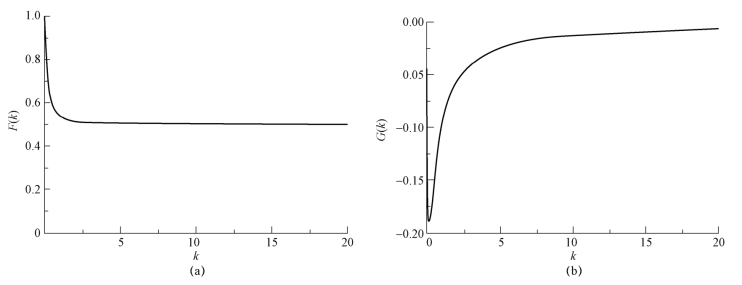
图6-17　Theodorsen函数

为了考虑流体黏性对流体作用力的影响，Munch基于不可压缩、湍流黏性流动的大量数值计算与实验结果进行曲线拟合，提出了Munch非定常动力模型，将流体对结构的附加作用力矩定义为

将式（6.2）在时域内进行离散，可得

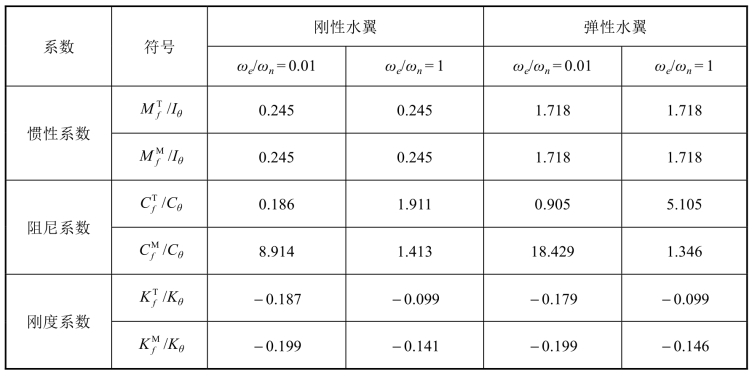
基于上述理论对两种不同结构物质参数和两种不同流体介质参数的结构流激振动特性进行分析，如表6-1所示。其中，ρs为结构密度，ξs为结构阻尼系数，ωθ为结构在真空中的特征频率，ωn为结构在水中的特征频率。采用的计算工况为来流速度5 m/s，雷诺数5×105。

表6-1　结构物质参数和流体介质参数

(www.daowen.com)

图6-18分别给出了在不同激励条件和流体介质中，数值计算的刚/弹性水翼扭转变形角度随时间的变化情况：当ωe/ωn=0.01时，表征外部激励频率远小于共振频率；当ωe/ωn=1时，外部激励等于共振频率。

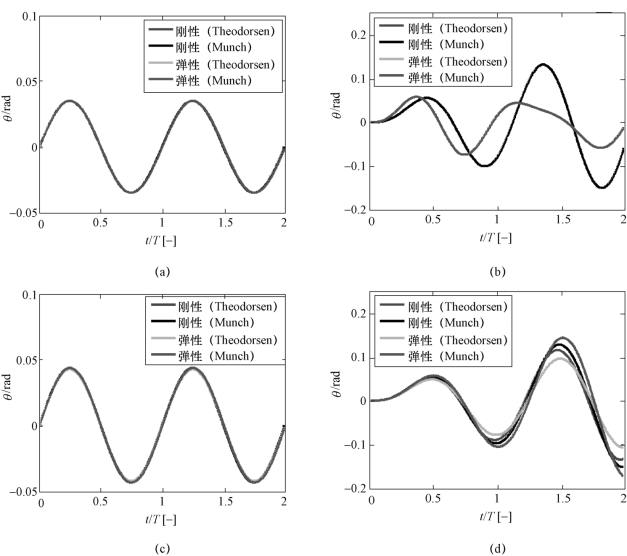
图6-18　不同流体介质和激励条件下，刚性与弹性水翼扭转变形角度随时间的变化

（a）ωe/ωn=0.01，流体介质为空气；（b）ωe/ωn=1，流体介质为空气；（c）ωe/ωn=0.01，流体介质为水；
（d）ωe/ωn=1，流体介质为水

对比图6-18（a）和（b）与图6-18（c）和（d）可知，当流体介质为空气时，采用Theodorsen模型和Munch模型数值计算得到的水翼扭转变形角度随时间的变化情况基本一致；当流体介质为水时，采用Theodorsen模型和Munch模型对翼型水弹性响应的数值计算结果出现差异，且共振激励频率下不同模型的数值计算结果差异比非共振激励频率下更为明显。造成这种差异的原因在于，空气黏性较小。因此，考虑了流体黏性的Munch模型与基于势流理论的Theodorsen模型的数值计算结果基本一致，而当流体介质为水时，水的黏性不可忽略。Theodorsen模型由于不考虑流体黏性而在一定程度上低估了结构的弹性变形量，从而导致Theodorsen模型和Munch模型的数值计算结果差异较大。

对比图6-18（a）和（c）与图6-18（b）和（d）可以看出，当结构所受外部激励的频率为非共振频率时，刚性和弹性水翼的扭转变形角度随时间的变化情况基本一致，均随外部激励发生周期性变化；当结构所受外部激励的频率为共振频率时，振幅明显大于非共振激励频率下的振幅，且刚性和弹性水翼发生共振时的振幅和频率相差较大，水翼在水中的弹性变形量呈明显发散趋势。这反映了当结构所受外部激励的频率接近系统固有频率时，系统振幅显著增大的共振现象，同时结构的材料属性对水弹性响应的振幅和频率影响较大。

图6-19给出了在基于Theodorsen模型和Munch模型数值预测流体作用力下，刚/弹性水翼产生的惯性力矩、阻尼力矩和刚度力矩随时间的演变情况，并与相同扭转变形角度下结构的固有惯性力矩、阻尼力矩和刚度力矩进行了对比。在本节的研究中，设定流体介质为水，外部激励频率为非共振频率，即ωe/ωn=0.01。表6-2给出了基于不同流体作用力模型计算得到的流-固惯性力矩、阻尼力矩和刚度矩系数之比。

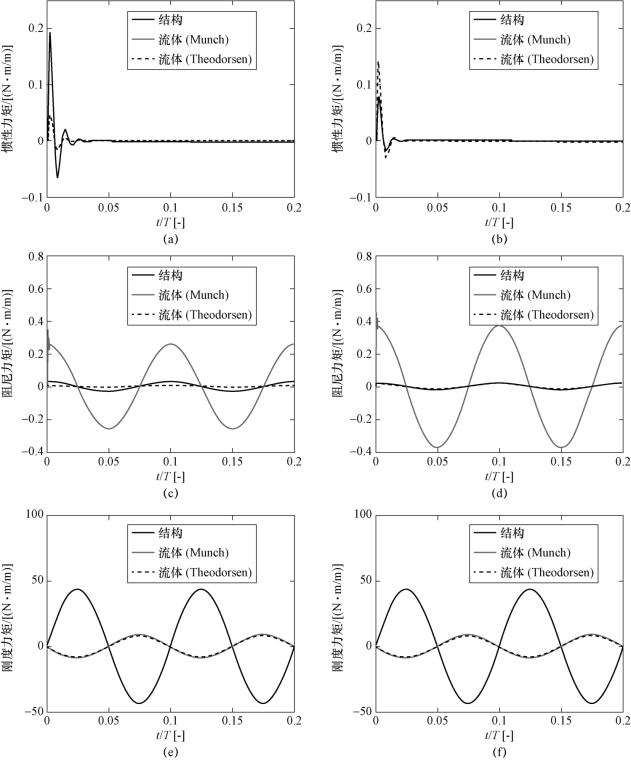
图6-19　结构固有惯性、阻尼和刚度力矩和流体作用力下的惯性、阻尼和刚度力矩随时间的演变情况（ωe/ωn=0.01）

（a）惯性力矩（刚性，ωe/ωn=0.01）；（b）惯性力矩（弹性，ωe/ωn=0.01）；（c）阻尼力矩（刚性，ωe/ωn=0.01）；
（d）阻尼力矩（弹性，ωe/ωn=0.01）；（e）刚度力矩（刚性，ωe/ωn=0.01）；（f）刚度力矩（弹性，ωe/ωn=0.01）

由图6-19（a）和（b）可知，对于相同结构，基于Theodorsen模型和Munch模型数值预测流体作用力下的惯性力矩随时间的演变规律相同，这是因为，由表6-2可知，基于Theodorsen模型和Munch模型计算流体作用力下的惯性系数相等，即，结合式（6.3）和式（6.5）可知，Theodorsen模型与Munch模型对流体作用力下的惯性系数项定义相同，惯性系数仅与流体密度和结构几何参数有关，与折合频率、雷诺数等无关。同时，流体作用力下的惯性力矩与结构固有惯性力矩随时间的演变呈同相分布，说明在水弹性响应的影响下，由流体与结构组成的弹性系统内部惯性作用加强。此外，由图6.5（a）和（b）不难发现，初始时刻，刚性水翼在流体作用下的惯性力矩小于结构的固有惯性力矩，而弹性水翼在流体作用下的惯性力矩大于结构的固有惯性力矩。结合表6-2可知，刚性和弹性水翼的流-固惯性系数比值分别为0.245和1.718，刚性水翼的密度较大，流-固密度比较小，因此刚性结构在流体作用力下产生的惯性作用力比弹性结构在相同作用力下的惯性作用力小。

由图6-19（c）和（d）可知，基于Theodorsen模型数值预测流体作用力下的阻尼力矩小于基于Munch模型数值预测流体作用力下的阻尼力矩。结合表6-2可知，不同流体作用力下刚性水翼流固阻尼系数比值分别为0.186（Theodorsen模型）和8.914（Munch模型），而对于弹性水翼，流-固阻尼系数比值则分别为0.905（Theodorsen模型）和18.429（Munch模型）。这是因为Theodorsen模型基于无黏势流假设，流体作用力的阻尼作用偏小。此外，采用Munch模型预测流体作用力下的阻尼力矩明显大于结构的固有阻尼力矩，两者同相分布，说明水弹性响应进一步增强了弹性系统的阻尼作用，其中流体作用力的阻尼作用强于结构的固有阻尼作用。

由图6-19（e）和（f）可知，基于Theodorsen模型和Munch模型数值预测流体作用力下的刚度矩随时间的演变情况基本一致，结合表6-2可知，采用不同模型预测流体作用力下的流-固刚度系数比值也很接近。这是由于结构的刚度系数较大，流-固刚度系数比值较小，因此，流体作用力下的刚度效应受水弹性响应影响较小。与惯性力矩和阻尼力矩不同的是，流体作用力下的刚度矩与结构的固有刚度矩呈反相分布，这说明水弹性响应在一定程度上削弱了弹性系统的刚度作用。

综合图6-19（a）～（f）可以看出，当外部激励频率为非共振频率时，结构的固有刚度矩远大于结构的固有惯性力矩、阻尼力矩以及流体作用力下的相应附加载荷，因此结构的刚度作用是影响结构水弹性响应的主要因素。同时，结构的固有惯性、阻尼和刚度力矩与流体作用下的相应附加载荷均处于同一数量级，因此流体与结构的相互作用不可忽略，尤其对于弹性水翼，由于流体作用力下的惯性、阻尼作用增大，流-固耦合算法的数值稳定性将对弹性水翼流-固耦合特性的数值计算结果产生更大的影响。

表6-2　不同流体作用力下的流-固惯性、阻尼和刚度系数之比

为了进一步研究激励频率对结构水弹性响应和流-固耦合特性的影响，图6-20对比了外部激励频率为共振频率（ωe/ωn=1）时，基于Theodorsen模型和Munch模型数值预测流体作用力下，刚/弹性水翼的惯性力矩、阻尼力矩和刚度矩随时间的演变情况。

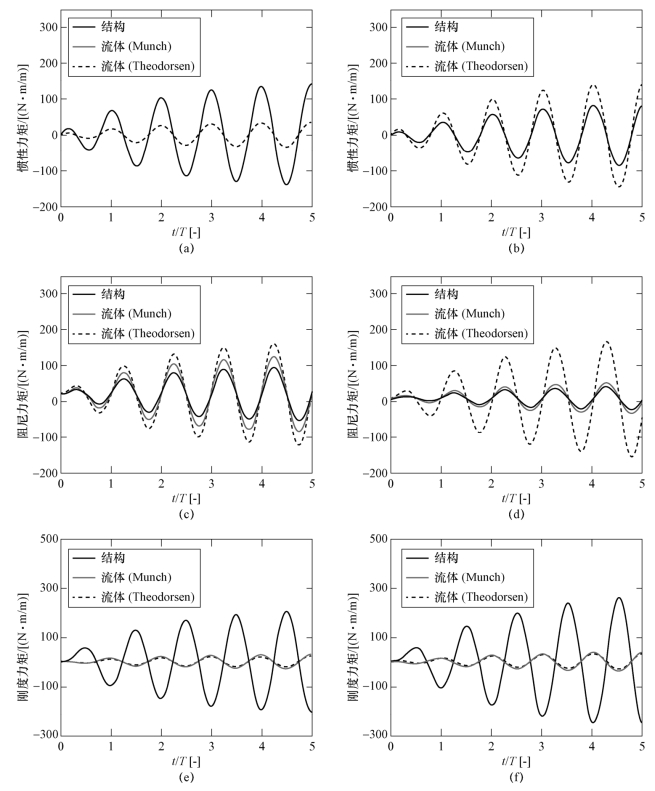
图6-20　结构固有惯性、阻尼和刚度力矩和流体作用力下的惯性、 阻尼和刚度力矩随时间的演变情况（ωe/ωn=1）

由于Theodorsen模型和Munch模型对流体惯性系数定义相同，由图6-20（a）和（b）可以看出，不同流体作用力下的惯性力矩随时间的演变情况相同，且由于刚性水翼的密度远大于流体的密度，而弹性水翼的密度与流体的密度相当，因此刚性水翼在流体作用力下产生的惯性力矩小于结构固有的惯性力矩，而弹性水翼在流体作用力下产生的惯性力矩大于结构固有的惯性力矩。由于流体惯性系数与折合频率无关，由表6-2可知，外部激励频率为共振频率时，数值计算得到的刚/弹性水翼流-固惯性系数之比分别为0.245和1.718，与外部激励频率为非共振频率时的计算结果一致。值得注意的是，基于无黏势流假设的Theodorsen模型是针对任意变形翼型简谐运动的推导结果，当激励频率较高，结构变形量较大时，采用Theodorsen模型的数值计算结果可靠性大大降低。由图6-20（c）～（f）不难发现，基于Munch模型的数值计算结果表明，结构固有阻尼力矩小于流体作用力下产生的阻尼力矩，且二者同相分步；结构固有的刚度矩大于流体作用力下产生的刚度矩，且二者呈反相分布，这与外部激励频率为非共振频率时数值计算得到的水弹性响应趋势是一致的。由表6-2可知，与外部激励频率为非共振频率时的数值计算结果相比，共振激励频率下，基于Munch模型数值预测流体作用力下的流固阻尼系数比和刚度系数比明显减小，流体的阻尼和刚度作用减弱。此外，结合图6-19（d）可知，当结构所受外部激励频率为共振频率时，结构的变形量呈现发散趋势，流体作用力也随时间的发展逐渐增大。综合图6-20（a）～（f）可知，当外部激励频率为共振频率时，弹性水翼固有的惯性、刚度力矩与流体作用力下产生的惯性力矩大小相当，说明除结构的刚度作用外，流体与结构的惯性作用对结构水弹性响应和流-固耦合特性的影响也较大。