模态是结构系统的固有振动特性，将结构自由振动系统解耦成N个正交的单自由度振动系统，即对应结构系统的N阶模态。各阶模态具有特定的固有频率、阻尼比和模态振型。模态分析的最终目标是识别系统的模态参数，为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。

在一般情况下，结构模态指“干模态”，即结构在不考虑周围环境介质影响真空状态下的模态。在实际计算中，结构都会被周围流体介质“包围”或者“环绕”。当周围流体密度很小如空气等时，其压缩性很大，对结构的模态影响较小，所以通常把结构在空气中的模态也视为“干模态”；当周围流体密度较大和结构处在同一个数量级（如水等）时，基本为不可压缩流体，对结构的模态影响较大，为了准确得到结构模态参数，必须考虑周围介质的影响，计算其“湿模态”。

在模态分析中，一般假设结构的刚度和质量恒定不变，不考虑阻尼作用且结构做自由振动。结构在水介质中的振动问题属于典型的流固耦合振动问题。在水力机械领域，国内外对水坝、储液容器、海洋结构等耦合问题进行了较为深入的研究。然而，对水轮机振动特性的研究相对还比较少，主要原因在于传统水轮机转轮尺寸、单机容量较小，叶片较为厚实，振动问题并不突出，没有引起太多注意。近年来，随着单机容量、尺寸及比转速的不断提高，新型材料的大量使用，相对刚度减弱，转轮叶片的水力振动问题日益突出，引起了国内外的广泛关注。此外，工程界也迫切希望能提供转轮在水介质中的振动特性，以保证合理进行水力设计、结构设计及安全稳定运行。

针对这些问题，过去主要是借助于实验来完成。模态测试技术是参数识别方法，其原理是在实际结构模态模型动态响应条件下，通过测试数据的处理分析，得到振动系统的模态频率等。在实验过程中，对静止状态下的结构进行人为激振，通过测量激励力与振动响应确定存在于激振点和测点之间的传递函数，建立传递函数矩阵，通过模态分析理论识别结构的模态参数，最终建立结构物的模态模型。图6-12所示为模态测试实验过程示意图。

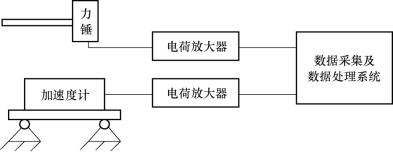
图6-12　模态测试实验过程示意图

目前，模态测试主要通过两种方法实现，即激振器实验和敲击法。实验中应注意激振点的选择、传感器连接及环境噪声抑制等问题。图6-13给出了模态实验测得水翼结构振动速度随时间的变化曲线，其中横坐标为时间，纵坐标为无量纲处理后的振动速度y=y′/ymax。基于振动速度随时间的变化曲线进行快速傅里叶变换得到振动频域图，如图6-14所示。与水翼结构在空气中的固有频率相比，由于水中附加质量的影响，水翼结构在水中的固有频率下降了65%。这是由于一阶弯曲固有频率和一阶扭转固有频率与系统总质量与弯曲/扭转刚度的比值成正比，空气中的流体介质质量可以忽略，而水中附加质量不可忽略。

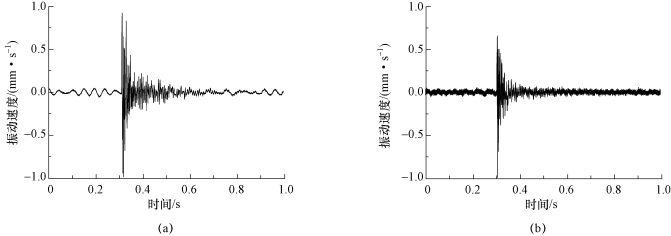
图6-13　振动速度随时间的变化曲线(www.daowen.com)

（a）水翼在空气中的振动响应；（b）水翼在水中的振动响应

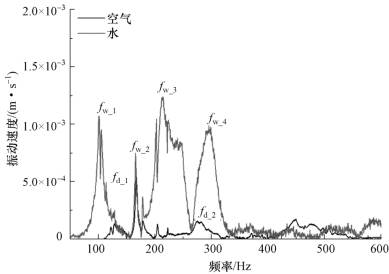
图6-14　空气中与水中的固有频率

然而用实验的方法来指导结构设计，周期长、成本高、易受外界因素干扰，且有些实验目前还无法进行，而工程设计又需要考虑结构在水中的自振特性，因而人们开始考虑用数值方法来研究。最初人们提出用数值计算方法求解结构在空气中的自振特性，然后根据经验乘以一个小于1的系数得出水中的自振频率。众多的研究表明，这与真实情况有较大的误差，因为结构在水中固有频率的降低与许多因素（如水的密度、黏度、可压缩性、静水压力、水的流速以及结构几何外形等）有关，而不能简单地用乘以一个系数的方法来处理。随着有限元等数值计算方法的不断成熟，一些学者开始尝试用有限元法计算结构在水介质中的振动特性。例如，Dubas借助有限元软件ANSYS计算了混流式水轮机在空气中的静、动态特性；Tomita采用有限元法建立了水轮机液固耦合振动有限元方程。1986年，程德林根据能量法和振动相似性理论，建立了水轮机在空气中固有频率与水中固有频率之间的关系式，用计算得到的水轮机在空气中的动态特性来分析在水中的特性。

很显然，这种方法存在很大的误差，并且其浸没系数必须通过模型实验才能确定。最近10年来，随着计算技术的发展，基于流固耦合理论的湿模态法在水力机械转轮动态特性分析中逐渐得到应用。朱世林等采用附加质量法计算了混流式水轮机在水介质中的振动特性，并且作了实验模态分析；王正伟等利用变分原理从理论上推导了转轮叶片在动水中振动的有限元方程；梁权伟、肖若富等利用能量法分析了转轮在水中的动态特性；何玲艳用有限元法计算了南水北调大型双吸泵转轮在空气和水中的模态。图6-15给出了数值预测的水翼前三阶湿模态振型及振动频率，并与实验结果进行了对比。结果表明，前三阶模态分别为一阶弯曲模态、一阶扭转模态和二阶弯曲模态，数值预测各阶模态频率与实验测量值基本吻合。

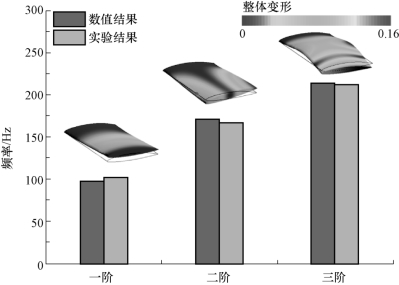
图6-15　数值预测的水翼前三阶湿模态振型及振动频率

这些成果为分析水力机械的流激振动，特别是在某些工况下的特殊振动奠定了基础。但是，在现有的湿模态计算时，基本上都没有考虑静水压力、转轮转速、流体流动、流体密度的变化、黏度及可压缩性等因素对转轮叶片在水介质中自振特性的影响，这将是流激振动研究面临的重大挑战之一。