近年来研究者在实验中发现，空穴断裂及脱落存在另外一种非定常机制。Ceccio等采用高速摄像和X射线技术研究了片状空化向云状空化转变规律，在不同工况下，存在两种非定常流动机制，即以空泡旋涡脱落为特征的回射流机制和以大尺度空穴结构瞬间溃灭为表现形式的泡状流激波机制。Reisman等和Arndt等在研究绕水翼空化脱落机理时，认为当σ/2α较小时，在空化区域内的类似间断面的泡状流激波是影响附着型空穴断裂及脱落的重要因素。已有的研究初步推断，泡状流激波间断面产生于尾部大尺度空泡团的溃灭压力波，当压力波传播到附着型空穴前缘时，会导致附着型空穴的断裂及空泡脱落。最近，Brennen和Ceccio的研究表明，在空化流动中，尽管主流纯液体具有低马赫数流动的特点，但在空化区域汽-液混相介质中，声速将会出现显著下降，最低声速出现在含汽率为0.5处。因此，空化汽-液混相区域流动可以达到10个当地马赫以上。随着空化数的降低，空穴内部的含汽量会增加，空化流体的声速会显著降低。当空化局部马赫数达到冲击波产生条件时，就会发生以大尺度空穴结构瞬间溃灭为特征的泡状流激波机制。Ganesh等通过在空穴区域设置障碍物的方式研究回射流机制与泡状流激波机制下空化不稳定性的差异。结果表明，设置障碍物可有效抑制回射流诱导空穴断裂及空泡脱落机制下的空化不稳定性，但是无法抑制泡状流激波机制下的空化不稳定性，这是由于泡状流激波厚度与空穴厚度相近；当泡状激波面推进到收缩-扩张段分离区域时，会造成大尺度空泡云的脱落。Wu采用流动可视化与瞬态压力测量的方法研究了收缩-扩张管道中的非定常空化流动现象。研究结果表明，附着型空化的周期性演化频率随着来流速度的增加而减小。在一定空化数下，随着主流速度的增加，空化流动结构由旋涡片状空化逐渐演化为以回射流为主导的片/云状空化，进而发展为以水汽激波主导的瞬态溃灭空化。两相气泡流激波在向上游推进过程中，移动的速度高于当地的声速，激波面推进前缘会产生了一个明显的压力波动，并随即产生片状空化的突然溃灭以及涡状空泡云。

下面，以绕NACA66型水翼两种典型工况为例，说明回射流机制（α=8°，σ=1.5，σ/2（α-α0）=4.52）与泡状激波机制（α=6°，σ=1.2，σ/2（α-α0）=4.58）表现形式的差异。

对于α=8°，σ=1.5，σ/2（α-α0）=4.52工况，片状空泡结构从水翼前缘向尾缘发展至x/c=0.8位置处，如图5-69（a）～（f）和图5-71（a）所示。在空泡发展过程中，空泡尾部形成反向射流并从空泡尾缘两侧分别向空泡前缘中心位置推进。当两束反向射流在翼型中截面汇合时，空泡尾部被切断，大尺度空泡团脱落并向下游移动，形成楔形空泡尾缘，如图5-69（g）所示。这一空泡脱落演变过程是由于流场逆压梯度导致反向射流引起的，大量学者对非定常空化流动特性的研究均是针对此脱落机理。

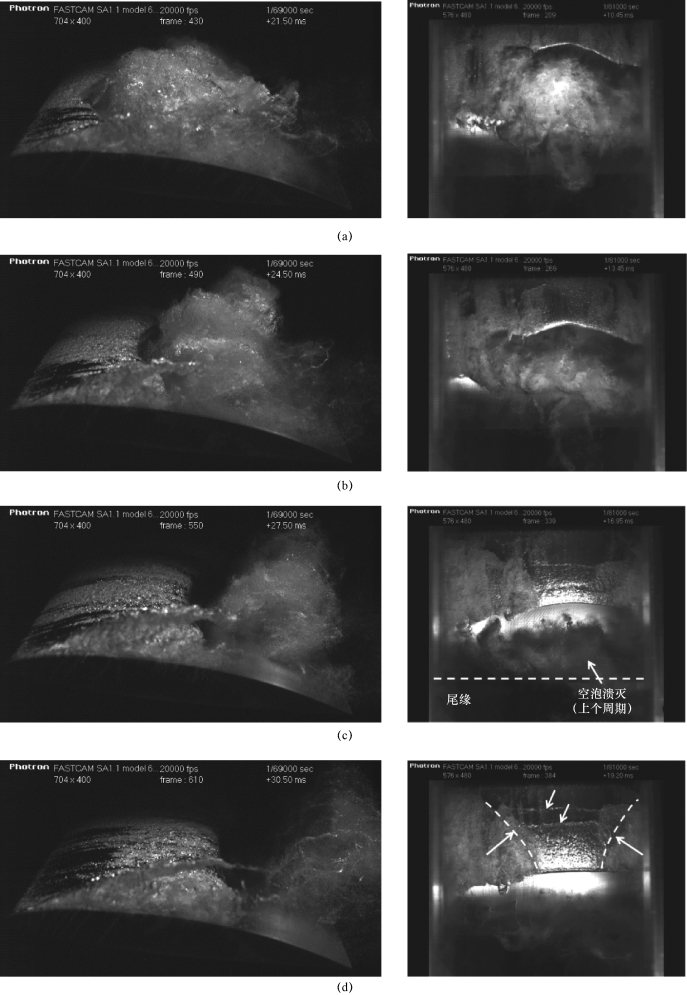
图5-69　空泡形态随时间的演变（α=8°，σ=1.5，σ/2（α-α0）=4.52）

（a）t1=t0；（b）t2=t0+15%T；（c）t3=t0+30%T；（d）t4=t0+45%T

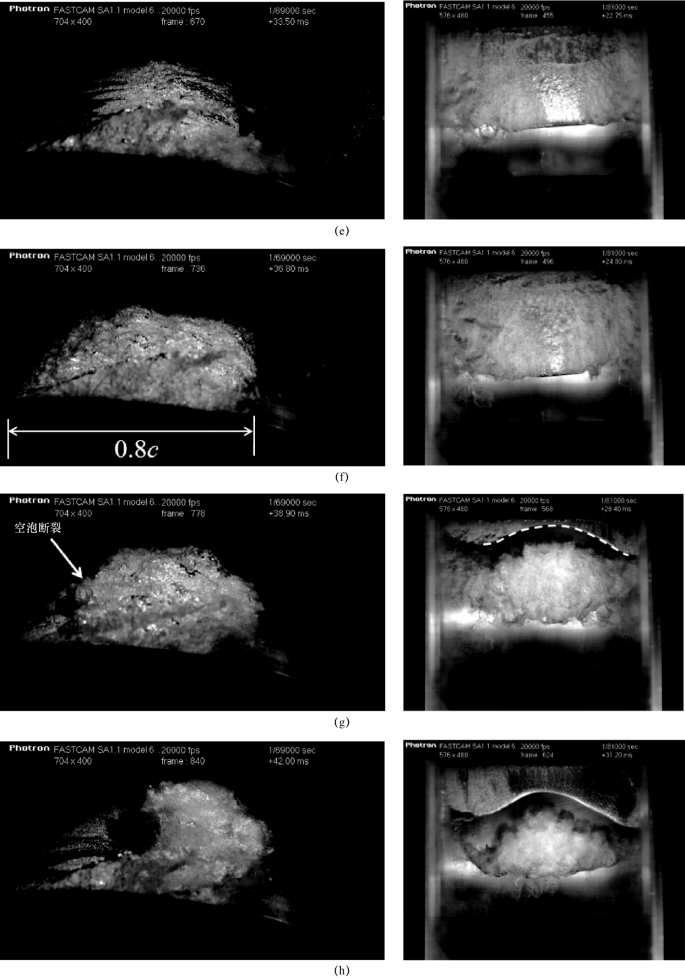
图5-69　空泡形态随时间的演变（α=8°，σ=1.5，σ/2（α-α0）=4.52）（续）

（e）t5=t0+60%T；（f）t6=t0+80%T；（g）t7=t0+90%T；（h）t8=t0+T

与α=8°，σ=1.5，σ/2（α-α0）=4.52工况相比，当空泡发展至尾缘时，即α=6°，σ=1.2，σ/2（α-α0）=4.58工况下，空泡呈现更为复杂的形态与脱落机理。如图5-70（a）和（b）所示，片状空泡结构首先在水翼前缘形成并沿水翼吸力面向尾缘发展，同时在空泡尾部形成反向射流。反向射流的形成导致空泡长度发生小范围的波动，波动范围约为0.2 c，如图5-71（a）所示。当空泡发展至0.9 c～1.0 c时，空泡尾缘变得十分不稳定，同时由于反向射流逆向发展至水翼前缘，与汽液交界面相互作用，导致空泡后半部分（0.5 c～0.9 c）卷曲形成大尺度云状空泡团，如图5-70（c）和（d）所示，大尺度空泡团脱落，空泡长度骤减至0.5 c左右，如图5-71（b）所示。水翼吸力面的附着空泡继续生长，如图5-70（d）和（e）所示，同时空泡发展速度增大，如图5-71（b）所示。这是由于反向射流的形成将附着在水翼吸力面上的空泡推离抬升，减小了空泡发展的流动阻力。当空泡尾缘大尺度空泡团脱落并向下游移动至水翼尾迹区域时，流场与空泡团内部的压力差导致空泡团的溃灭，如图5-70（e）所示。此时，水翼吸力面的附着空泡几乎在同一时刻停止生长，且由尾缘向前缘方向依次迅速溃灭，直至水翼吸力面空泡完全消失，如图5-70（f）～（h）所示，空泡长度骤减至最小值，如图5-71（b）所示。这一附着空泡的二次溃灭现象是由于水翼下游尾迹区域，受水翼吸力面与压力面压差的影响，进一步加剧了流场空泡内外的压力梯度，空泡团溃灭形成的冲击波引起吸力面压力分布的急剧变化，从而导致吸力面附着型残余空泡的二次溃灭。这一现象在Ganesh、Leroux等的前期研究中也有所提及。

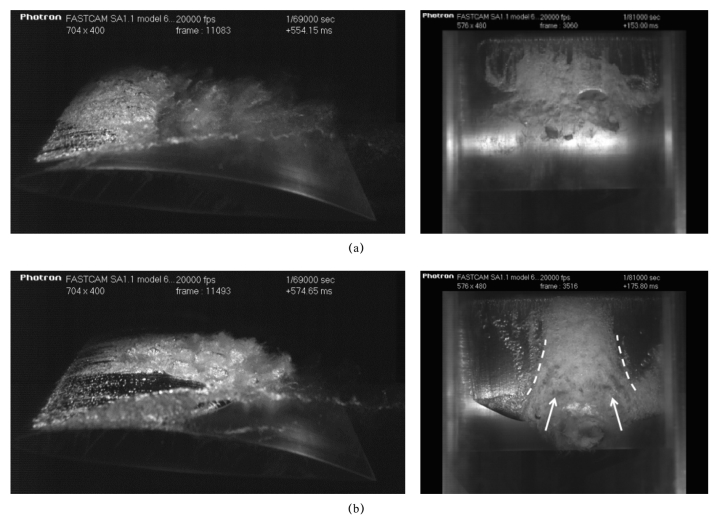
图5-70　空泡形态随时间的演变（α=6°，σ=1.2，σ/2（α-α0）=4.58）

（a）t1=t0+10%T；（b）t2=t0+40%T

(www.daowen.com)

图5-70　空泡形态随时间的演变（α=6°，σ=1.2，σ/2（α-α0）=4.58）（续）

（c）t3=t0+60%T；（d）t4=t0+70%T；（e）t5=t0+80%T；（f）t6=t0+90%T

图5-70　空泡形态随时间的演变（α=6°，σ=1.2，σ/2（α-α0）=4.58）（续）

（g）t7=t0+92%T；（h）t8=t0+95%T

对比两种云状空化发展过程发现，空泡脱落过程受两种机制联合影响：一是由于空泡尾部逆压梯度导致反向射流，如图5-69（b）和5-70（d）所示；二是由于大尺度云状空泡团溃灭形成冲击波，如图5-69（f）～（h）和5-70（d）和（e）。当空泡发展至水翼尾缘，即最大空泡长度大于1.0c时，空泡溃灭位置位于水翼下游尾迹区域，水翼吸力面与压力面压差加剧了流场空泡内外的压力梯度，从而空泡溃灭导致的冲击波起到主要作用，同时伴随有水翼结构强烈的振动与噪声。

图5-71给出了α=8°，σ=1.5，σ/2（α-α0）=4.52和α=6°，σ=1.2，σ/2（α-α0）=4.58两种不同云状空化条件下的振动速度测量结果。为了更好地研究非定常空化流动对结构振动的调制作用，应用Hilbert函数获取了振动速度信号包络线，如图5-71所示。两种工况下的振动速度信号均表现出显著的周期特性，但α=6°，σ=1.2，σ/2（α-α0）=4.58工况下的振动速度幅值远大于α=8°，σ=1.5，σ/2（α-α0）=4.52。其中，在α=6°，σ=1.2，σ/2（α-α0）=4.58工况下，典型周期内的振动速度演变过程主要由两部分构成，振动速度信号包络线随时间逐渐增加，同时伴随小幅波动；随后振动速度信号波动范围大幅增加，同时振动速度信号包络线随时间推移逐渐减小。在α=8°，σ=1.5，σ/2（α-α0）=4.52工况下，振动速度随时间周期性先增加后减小，波动幅值相对较小。基于Hilbert函数计算得到的振动速度信号包络线进行快速傅里叶变换，如图5-72所示，两种工况下的主要振动频率分别为14 Hz和44 Hz。

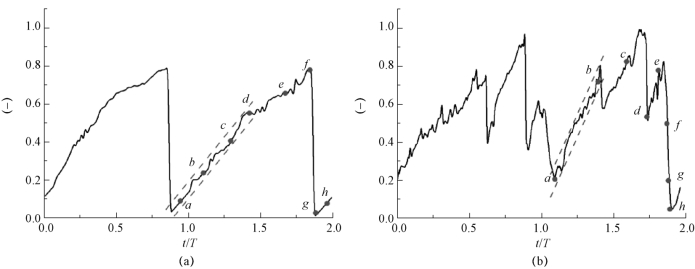
图5-71　空泡长度随时间的演变

（a）α=8°，σ=1.5，σ/2（α-α0）=4.52；（b）α=6°，σ=1.2，σ/2（α-α0）=4.58

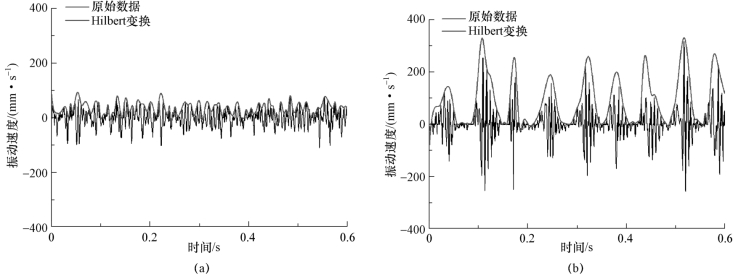
图5-72　振动速度随时间的演变

（a）α=8°，σ=1.5，σ/2（α-α0）=4.52；（b）α=6°，σ=1.2，σ/2（α-α0）=4.58