为了更好地预测和分析非定常流场结构的动态演变规律，引入一种有限时间Lyapunov指数（Finite-Time Lyapunov Exponents，FTLE）流场分析技术，利用拉格朗日拟序结构（Lagrangian Coherent Structures，LCS）分析方法对流场结构及流动特性进行了研究。

在传统欧拉体系下，速度梯度张量可分解成对称张量（应变率张量Sij）和反对称张量（涡张量Ωij）：

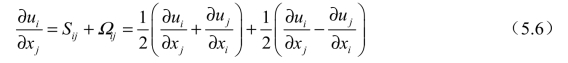
式中，i和j代表不同的方向。

基于欧拉体系的涡旋判据包括涡度ω、Q等，分别定义为

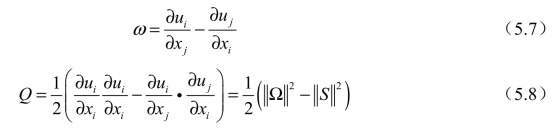
另一类涡旋辨识准则基于拉格朗日体系，以流体质点在流场中对流特性的时间积分为主要考虑因素，无须使用速度梯度张量。因此，对速度场的空间分辨能力要求较低，有限时间Lyapunov指数即是其中的一种。

一般动力系统可表示为

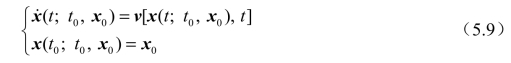
式中，t为时间（自变量）；x表示系统状态（因变量）。

对于任意空间点x0，利用空间梯度求解柯西-格林应变张量：

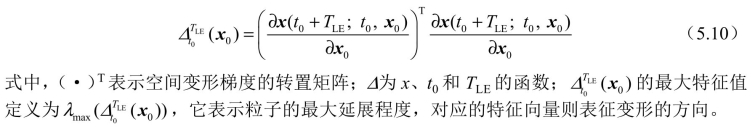
在有限时间TLE内，FTLE定义为

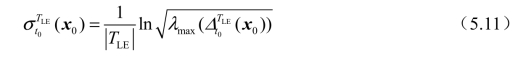
FTLE场是一个标量场，它反映了流体的特性。当相邻粒子以不同运动特性运动时，会导致FTLE场中出现突出的“脊线”结构，这种结构称为拉格朗日拟序结构（LCS）。通常，FTLE和LCS一起被认为是研究流场结构的后处理技术，利用LCS可以分割不同运动特性的流场，从而捕捉潜在流场的动态力学和几何学特性。

下面将用两个算例，来说明基于拉格朗日拟序结构分析方法在复杂旋涡结构表征中的应用。

5.5.2.1　方腔通气气-液两相流场结构分析

采用长方体方腔模型为研究载体，长方柱体内盛有一定量的水，其初始状态是静止的，且上表面为自由液面，底板正中央布置有一直径为1 cm的通气孔，通气量为48 L/h，如图5-50所示。网格划分采用六面体结构化网格，在通气孔附近采用O形网格，并在流域中间进行网格加密，如图5-51所示。

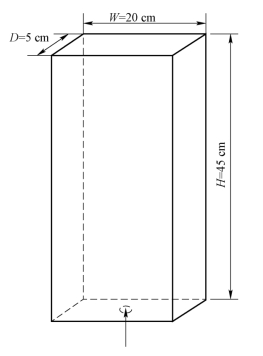
图5-50　计算域及边界条件设置

图5-51　网格示意图

基于数值计算结果，采用拉格朗日拟序结构分析方法，对长方柱体内的流场涡结构进行分析。定义无量纲时间t*=t/t∞，其中参考时间t∞=0.5 s（10个时间步）。根据方腔通气气-液两相流的流动特点，将方腔通气过程分为两个阶段。

1.通气起始阶段

图5-52（a）给出了通气起始阶段长方柱体内流场气相体积分数云图和流场流线分布情况。可以发现，气体经喷气孔进入长方柱体内，并在水中形成气束。气束从喷气孔沿竖直方向发展，长度不断增加，同时气体出流导致气束两侧液相流体中形成对称涡结构分布，涡结构随着气束长度的增加而增大，最终在气泡束左右两侧形成两个对称分布的大旋涡。图5-52（b）和图5-52（c）分别给出了常用的涡流结构判别标准ω分布和Q分布云图。从ω分布云图可以看出，ω关于喷气孔中心线呈明显对称带状分布，并且随着气束的增长而增长，方向相反的ω分布区域之间形成明显的边界。这是因为，在静止的液体流场中，沿喷气孔中心线气体流动方向存在很大的速度梯度，ω分布不能区分由于纯剪切流动引起的涡量和由于旋转运动引起的涡量，因而容易高估涡流的强度，因此也说明ω分布与涡并不等同。由式（5.8）可知，伽利略第二不变量Q为正值时，表示旋转运动强于轴向形变，可以此判别涡流所在区域，而正值越大，表示涡流的旋转运动越强。由图5-52（c）Q分布云图可知，相对于涡度ω在靠近气束区域的高估，Q在此区域有最小值，而在旋涡中心Q具有最大值。随着气束从喷气孔向出口边界处发展，Q分布反映的旋涡中心区域位置不断升高，这与图5-53（a）反映的趋势一致。图5-52（d）给出了FTLE分布云图，计算FTLE的积分时间TLE=1.5 s。从图中可清楚地观察到LCS的分布位置和形状。比较图5-52（a）和图5-52（d）可知，LCS并没有位于气-液交界面上，而是位于液相随气泡束流动的主流通道边界上，将气泡束周围的液相主流区和液相回流区分开。结合图5-53所示t*=2时刻部分质点经过时间TLE后的运动轨迹图可知，LCS内侧（区域B）靠近气泡束的液体随气相流向下游，为液相主流区域；LCS外侧（区域A）远离气泡束的液体反向逆流，向喷气孔方向运动，为液相回流区域。这个由LCS描绘出的主流与回流之间的运动边界很难通过常规的欧拉法进行描述。

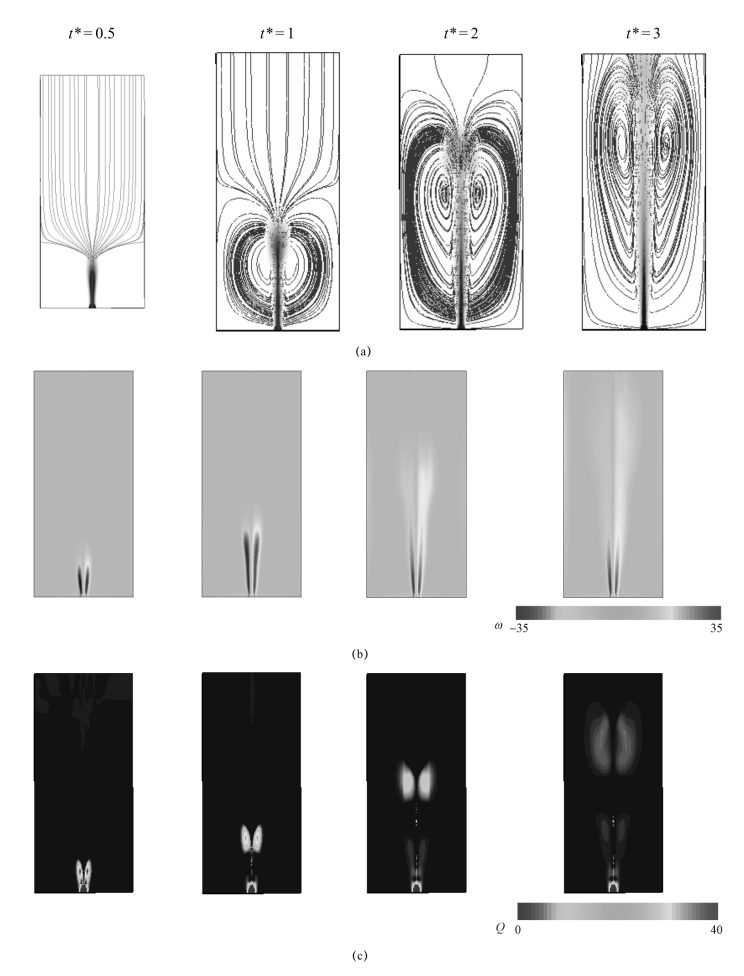
图5-52　通气起始阶段长方柱体内流场气相体积分数、流线分布、ω分布，Q分布和FTLE分布情况

（a）流场气相体积分数云图和流场流线分布图；（b）ω分布云图（定义逆时针为负，顺时针为正）；
（c）Q分布云图

图5-52　通气起始阶段长方柱体内流场气相体积分数、流线分布、ω分布，Q分布和FTLE分布情况（续）

（d）FTLE分布云图

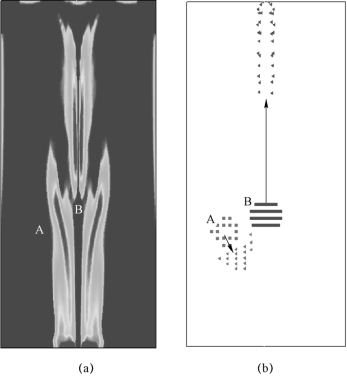
图5-53　t*=2时刻部分质点运动轨迹

（a）FTLE云图；（b）粒子始末位置

2.通气发展阶段

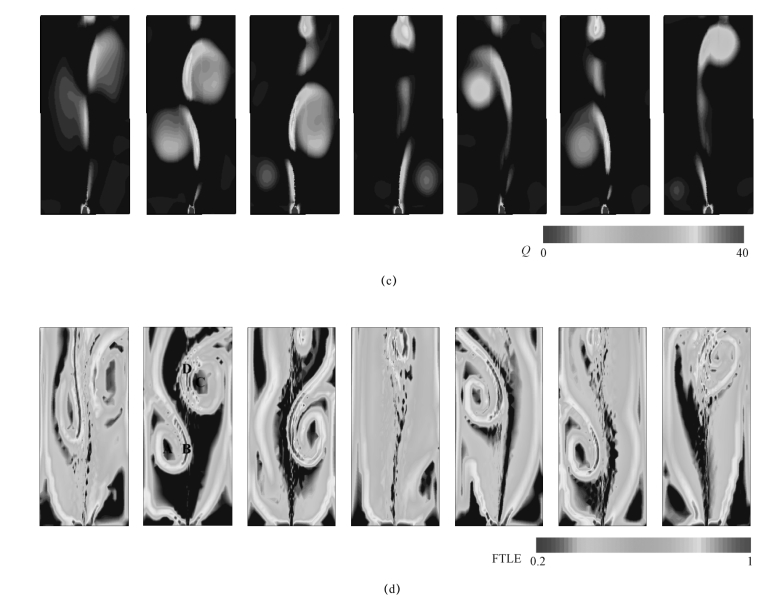
经过一段时间的发展，气泡束左右两侧对称分布的大旋涡基本保持稳定。随后，气泡束开始出现周期性摆动，伴随着其摆动，自由液面处的两个旋涡沿着气泡束的左右两侧交替向方腔底部运动，如图5-54（a）所示。ω分布和Q分布云图如图5-54（b）、图5-54（c）所示。观察发现，ω始终分布于气泡束两侧的气液交界面上，并随气泡束的摆动而摆动，ω分布较好地体现了气液交界面上由于速度梯度导致的流场结构变化，但无法体现流场的旋涡结构随时间的演变。由图5-54（c）可知，Q分布能较好地捕捉流场的旋涡中心，随着气泡束的周期性摆动，Q的最大值区域沿着气泡束的左右两侧向喷气孔运动，对应图5-54（a）中自由液面处的两个旋涡沿着气泡束的左右两侧交替向方腔底部运动过程。为了更清晰地给出流场涡结构的演变过程，图5-54（d）给出了通气发展阶段的FTLE场演变过程，其中计算FTLE的积分时间TLE=4.5 s。对比图5-54（b）～（d）可知，相比于欧拉体系的涡辨识方法，FTLE方法用具有拉格朗日性质的物质线显示旋涡边界，无须人为定义判别阈值，因此具有客观性。由于随着时间的周期性演变，流场开始有了不对称的动态行为，FTLE可表示流场中各质点的动态趋势，而非限于当前的流场。随着时间的推移，高FTLE值区域会与低FTLE值区域卷曲交错，进而形成“脊”状结构，即拉格朗日拟序结构（LCS），它代表该区域中无限相邻的质点，经过流场的拉扯、卷曲和交错等，将发散至较大的距离。这一现象描述为涡流拉扯，表明了LCS在流场结构分析中的独特之处。此外，LCS卷曲在涡中心的附近，但并未延伸至中心，表征质点经过流场拉扯后的发散程度。图5-55给出了图5-54（d）中t*=76时刻区域A、C（涡中心区域）和B、D（LCS所在区域）的部分质点经过时间TLE后的运动轨迹。不难发现，区域A、C中的质点仍基本保持原有相对位置关系，间距变化较小，对应低FTLE值区域；区域B、D中的质点随着速度场的周期性变化，被分散至涡中心两侧位置，对应高FTLE值区域，与LCS反映的流场结构一致。

图5-54　通气发展阶段长方柱体内流场气相体积分数、流线分布、ω分布、Q分布和FTLE分布情况（见彩插）

（a）流场气相体积分数云图和流场流线分布图；（b）ω分布云图（定义逆时针为负，顺时针为正）

(www.daowen.com)

图5-54　通气发展阶段长方柱体内流场气相体积分数、流线分布、ω分布、Q分布和FTLE分布情况（续）（见彩插）

（c）Q分布云图；（d）FTLE分布云图

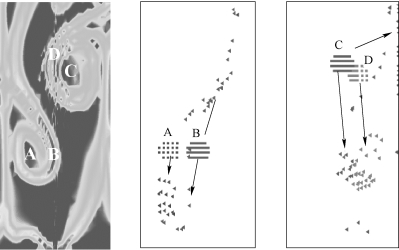
图5-55　t*=76时刻部分质点运动轨迹

5.5.2.2　云状空化流场结构分析

图5-56给出了计算得到的云状空穴流动形态随时间的准周期性变化过程，并和实验结果的对比情况。从图中可以看出，数值计算结果和实验结果相吻合，准确地描述了附着型空穴的生长-反向射流的发展-　空穴的断裂的准周期变化过程。根据文献［10］可知，该工况下的云状空化的发展周期约为Tref=40 ms。在t=5%Tref时刻，在水翼前缘处形成透明状附着型空穴，并处于持续增长状态。当附着型空穴覆盖整个吸力面时，在空穴尾部产生逆时针的空化旋涡，进而在紧贴壁面的区域内诱导了一股指向上游的反向射流，并持续向上游运动，如t=63%Tref时刻。当反向射流到达空穴前缘附近时，与主流相遇，导致附着型空穴的断裂；断裂部分沿顺时针方向旋转并向下游运动，逐渐发展成为脱落的空泡云，如t=81%Tref时刻。

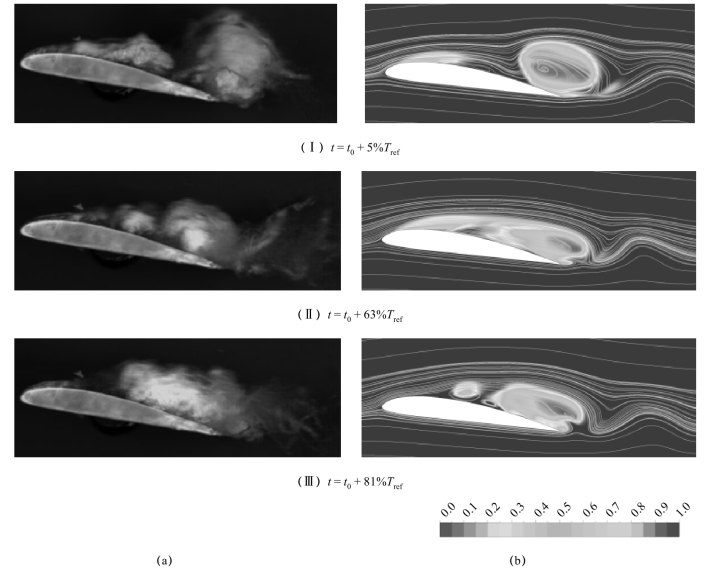
图5-56　计算和实验结果比较（见彩插）

（a）实验空泡形态图；（b）计算汽相体积分数图

由于上述附着型空穴的生长-反向射流的发展-空穴的断裂过程较为复杂，为了更准确地分析云状空化流场结构演变规律，将上述过程分为3个阶段：（Ⅰ）附着型空穴发展阶段（0～28%Tref）；（Ⅱ）反向射流向前运动阶段（28%～75% Tref）；（Ⅲ）脱落空化云的形成阶段（75%～100% Tref）。在不同阶段，空化发展具有不同的特点，为了进一步分析云状空化流动机理，下面采用基于拉格朗日体系的方法对每个阶段内的非定常流场结构进行描述。

1.附着型空穴发展阶段Ⅰ

在附着型空穴发展阶段，上个空化发展周期内的大尺度脱落空泡脱离水翼表面，前缘的附着型空穴逐渐发展并覆盖整个吸力面。

图5-57给出了附着型空穴发展阶段的FTLE云图，积分时间为附着型空穴TLE_I=28%TREF，图中FTLE取值根据最大值进行无量纲化处理。从图5-57中可以看出，在远离水翼表面的主流区域，FTLE取值为零，这是由于在均匀来流的作用下，该区域内部流体质点具有相同的运动状态，相邻流体质点的距离不随时间的变化而发生改变。从图5-57中还可以看出，在水翼吸力面附近的空化核心区域，FTLE分布和主流区域相差较大；这是由于附着型空穴的发展，导致空穴内部流体质点的运动规律与主流具有显著不同。

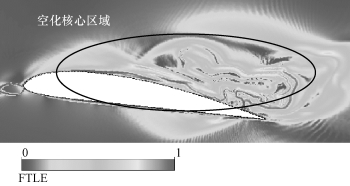
图5-57　阶段Ⅰ的FTLE和LCS分布（见彩插）

FTLE场的最大值称为LCS，其“脊”特性可以更清晰地展现流动细节。图5-58给出了基于附着型空穴发展阶段FTLE分布得到的LCS分布情况。从图中可以看出，空化核心区域存在两条主要LCS（图中红色曲线所示），两条LCS从上游开始，在水翼前缘发生分离，沿水翼吸力面发展的LCS在吸力面中部附近与水翼表面发生分离，定义为前缘拉格朗日拟序结构（Leading Edge Lagrangian Coherent Structure，LE-LCS）。沿水翼压力面发展的LCS绕过水翼尾缘并沿着吸力面向前缘延伸，在水翼尾缘附近发生分离，定义为尾缘拉格朗日拟序结构（Trailing Edge Lagrangian Coherent Structure，TE-LCS）。

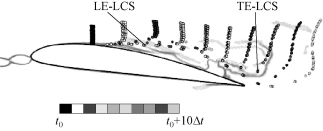
图5-58　阶段Ⅰ的LCS分布和粒子轨迹（见彩插）

在附着型空穴发展阶段，LE-LCS表示前缘分离涡的边界，这是由于前缘分离涡内部流体质点无法越过旋涡边界，从而在旋涡边界处形成“脊”结构。从图5-58中可以看出，LE-LCS延伸到水翼尾缘附近，表明前缘分离涡延伸到水翼尾缘附近，与附着型空穴相对应。TE-LCS表示水翼尾缘旋涡结构的边界，从图5-58中可以看出，TE-LCS和LE-LCS在水翼尾缘附近汇合并共同向下游延伸，在该阶段内水翼尾缘附近存在未完全脱离水翼尾缘的大尺度空泡云，有关该空泡云的形成和演变规律将在脱落空化云的形成阶段进行详细论述。

考虑到FTLE和LCS方法是对整个附着型空穴发展阶段进行积分，具有历史效应。为了进一步突出瞬态时间点的流动细节，引入基于拉格朗日体系的粒子追踪方法对附着型空穴的发展进行描述。为了分析附着型空穴的发展过程，在水翼吸力面距离前缘20%弦长位置处，沿法向布置示踪粒子，黑色表示粒子初始位置，其他不同颜色表示不同时刻示踪粒子的位置，如图5-58所示，Δt=2%Tref。从图中可以看出，远离水翼表面的示踪粒子在均匀主流的作用下向下游运动，运动规律基本一致；靠近水翼表面的示踪粒子，在附着型空穴的影响下，向下游的运动明显滞后于均匀主流作用下的示踪粒子；在近壁面位置，位于TE-LCS附近的示踪粒子被卷入附着型空穴内部，其运动规律和主流作用下的示踪粒子具有显著不同。该部分示踪粒子运动轨迹指向水翼尾缘，反映了附着型空穴的持续增长并覆盖水翼吸力面的发展过程，如图5-58所示。

2.反向射流向前运动阶段Ⅱ

在反向射流向前运动阶段，水翼尾部附近产生了液相的反向射流，并沿水翼表面逐渐向前缘推进。

图5-59给出了反向射流向前运动阶段的FTLE云图，积分时间为附着型空穴TLE-Ⅱ=47%Tref，图中FTLE取值根据最大值进行无量纲化处理。从图中可以看出，空化核心区域的FTLE分布和附着型空穴发展阶段有所不同，较大取值FTLE边界更为光滑。图5-59中红色曲线是该阶段的LCS分布情况，从图中可以看出，在反向射流向前运动阶段，LE-LCS和TE-LCS均延伸至水翼吸力面中部附近，较好地描述了附着型空穴较为光滑的边界。从图中还可以看出，水翼吸力面中部附近存在LE-LCS和TE-LCS的混合区域（Mixing region），该混合区域对应于反向射流和附着型空穴的相互作用位置。为了进一步分析反向射流和附着型空穴的作用机理，下面采用粒子追踪方法对流场结构进行分析。

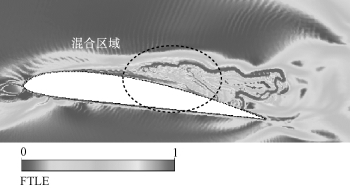
图5-59　阶段ⅡFTLE和LCS分布（见彩插）

根据上述混合区域的位置，在水翼吸力面距离前缘70%弦长位置处，沿法向布置示踪粒子。图5-60给出了不同时刻下的示踪粒子位置，黑色表示初始位置。图5-60还给出了该阶段内的LCS分布情况，从图中可以看出，初始时刻，示踪粒子位于TE-LCS内部，表明示踪粒子全部位于附着型空穴内部，运动规律不受主流的影响。从图中还可以看出，远离水翼表面的示踪粒子向下游运动，而靠近水翼表面的示踪粒子首先向上游运动，两种相反的运动方向反映了附着型空穴内部的顺时针旋涡结构。靠近水翼表面粒子首先向上游运动，这和反向射流相对应，当粒子抵达水翼前部附近时被卷入附着型空穴内部的旋涡结构，逐渐远离水翼表面并向下游运动。

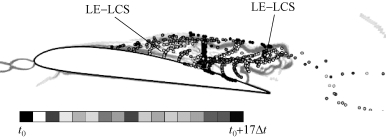
图5-60　阶段ⅡLCS分布和粒子轨迹（见彩插）

3.脱落空化云形成阶段Ⅲ

在脱落空化云形成阶段，附着型空穴在反向射流的作用下发生断裂，附着型空穴断裂部分逐渐向下游运动，发展成云状空泡。

图5-61给出了脱落空化云形成阶段的FTLE云图，积分时间为附着型空穴TLE-Ⅲ=25%Tref，图中FTLE取值根据最大值进行无量纲化处理。从图中可以看出，空化核心区域的FTLE分布和反向射流向前运动阶段基本一致，但水翼吸力面中部附近不存在LCS的混合区域。这表明，在脱落空化云形成阶段，水翼近壁面附近的反向流动和附着型空穴没有发生相互作用，这和附着型空穴的断裂相一致。为了进一步分析空化云的形成机理，下面采用粒子追踪方法对流场结构进行分析。

图5-61　阶段ⅢFTLE和LCS分布（见彩插）

为了捕捉附着型空穴的断裂以及空化云的形成过程，在水翼吸力面距离前缘20%弦长位置处，沿法向布置示踪粒子。图5-62给出了不同时刻下的示踪粒子位置，黑色表示初始位置，图5-62还给出了该阶段内的LCS分布情况，从图中可以看出远离水翼表面的示踪粒子首先在主流的作用下保持相同的运动状态，粒子相对位置保持不变。但是，随后该部分示踪粒子相对位置发生显著变化，这是由于附着型空穴的脱落部分在其内部旋涡结构的作用下逐渐发展成为空化云，从而对周围的流场产生影响，导致示踪粒子相对位置的变化。从图5-62还可以看出，靠近水翼表面的示踪粒子迅速被卷入附着型空穴断裂部分，运动轨迹反映了空化云的形成过程。

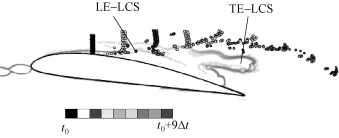
图5-62　阶段ⅢLCS分布和粒子轨迹（见彩插）

上述研究采用基于拉格朗日体系的有限时间李雅普诺夫指数（FTLE）、拉格朗日拟序结构（LCS）和粒子追踪方法对绕水翼典型非定常云状空化流场结构进行研究。定义了前缘拟序结构和尾缘拟序结构，在不同的空化发展阶段，两种拟序结构相互作用并呈现不同的分布规律：

（1）在附着型空穴发展阶段，LE-LCS延伸到水翼尾缘附近，与附着型空穴相对应。TE-LCS和LE-LCS在水翼尾缘附近汇合并共同向下游延伸，与脱落空化云对应。

（2）在反向射流向前运动阶段，水翼吸力面中部附近存在LE-LCS和TE-LCS的混合区域，该混合区域对应于反向射流和附着型空穴的相互作用位置。粒子追踪方法反映了反向射流以及附着型空穴内部的旋涡结构。

（3）在脱落空化云形成阶段，水翼吸力面中部附近不存在LCS的混合区域，反映了附着型空穴的断裂，粒子追踪方法反映了附着型空穴在内部旋涡结构作用下逐渐发展成脱落空化云的过程。