图5-33给出了在无空化（σ=2.00）和云状空化（σ=0.80）工况下，实验与数值计算的沿主流方向时均速度u的分布云图。实验与数值计算的结果均表明，在无空化阶段，绕水翼的速度分布分为两个明显的特征区域：一是水翼前缘附近的主流区；二是水翼尾部的低速区域。随着空化数的降低，速度分别表现出明显的特征差异，即当处于云状空化状态时，在水翼吸力面后部区域的空化核心区域内的速度大约在2.5 m/s，远小于主流速度，且存在较大的速度梯度，并向后扩展形成尾流。

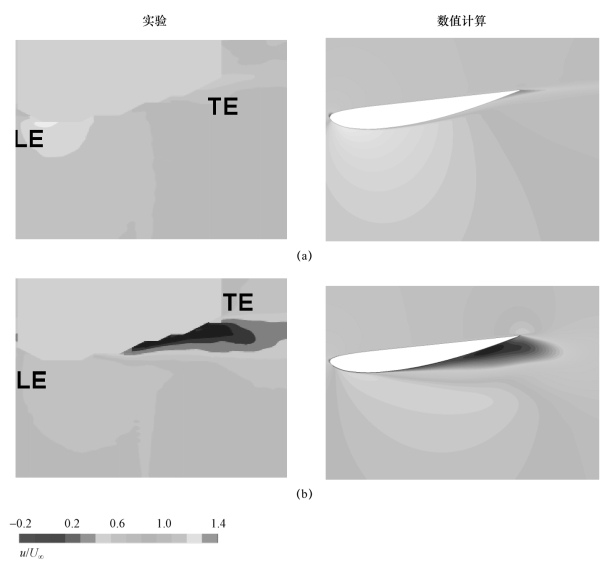
图5-33　水翼吸力面上的时均速度分布（α=8°，Re=7×105）

（a）无空化（σ=2.00）；（b）云状空化（σ=0.80）

图5-34和图5-35分别给出了实验与数值计算得到无空化（σ=2.00）和云状空化（σ=0.80）流场下，在如图5-34所示的特征位置处（x/c为0.2、0.4、0.6、0.8和1.0），沿主流方向速度u的时均、最大概率和标准差值随距水翼壁面距离y/c的分布。从图中可以看出，在两种工况下，绕水翼的速度分布存在较大的差异，尤其在水翼尾缘处。当σ=2.00时，时均速度分布与最大概率密度分布较为接近，速度的标准差接近于零，仅在水翼尾缘的近壁区域内存在一定的差别，这是由于尾涡引起了流场结构的小幅波动，数值计算结果与实验结果有较好的吻合。当σ=0.80时，在空化核心区域内，速度的时均与最大概率分布存在较大的不同。通过比较σ=2.00和σ=0.80在相同截面上的速度分布可以看到，当处于云状空化状态时，随着x/c的增大，速度湍流边界层的随之增厚，速度的标准差值有显著的增加，说明流场结构的非定常特性得以增强。在水翼尾缘处（x/c=0.6～1.0），速度的最大概率分布存在更为显著的反向射流。复杂的空化流场结构导致了速度的时均分布与最大概率分布存在较大的差异，速度值的非定常变化趋势不再满足高斯分布，这与σ=2.00时的流场特性有本质的不同。云状空化流场存在较强的非定常特性，对其流场速度进行时均处理往往会忽略空化流场中的尺度结构信息，速度在最大正值与最小负值之间存在间歇性的振荡。在一定程度上，近壁剪切区域内的时均速度分布不能很好地揭示非定常空化流动中的反向射流现象。标准差反映了不同时刻测量点间的离散程度，从一个侧面说明了流动非定常特性。从图5-34和图5-35中可以看出，当σ=2.00时，速度标准差较小，尤其在水翼前缘附近，说明此处流场结构较为稳定；当σ=0.80时，其速度标准差较大，尤其在水翼尾缘附近。与σ=2.0的工况相比，当σ=0.80时，尽管数值计算的结果与实验测量值存在一定的偏差，但数值计算结果合理地预测了空化效应对流场速度的影响。

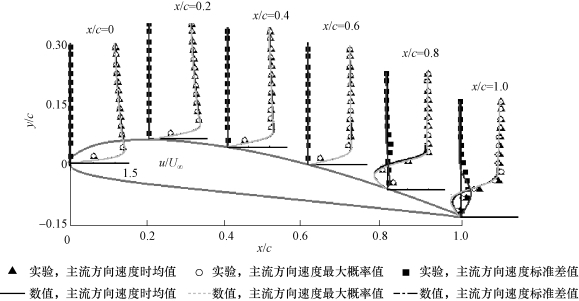
图5-34　沿主流方向速度u的时均、最大概率、标准差值沿距壁面距离y/c的分布（σ=2.00，α=8°，Re=7×105）

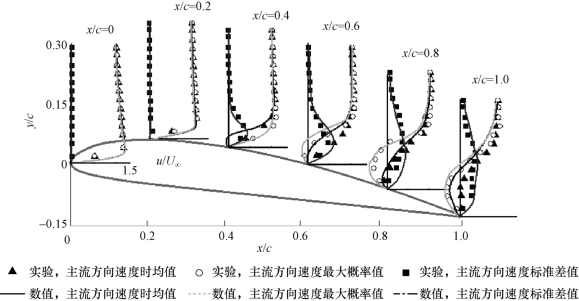
图5-35　沿主流方向速度u的时均、最大概率、标准差值沿距壁面距离y/c的分布（σ=0.80，α=8°，Re=7×105）

图5-36进一步给出了α=8°时，不同空化阶段绕水翼周围的时均湍流脉动强度分布。这里，湍流脉动强度I定义为

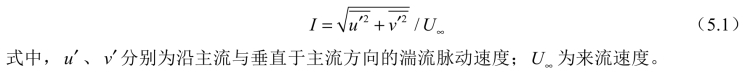
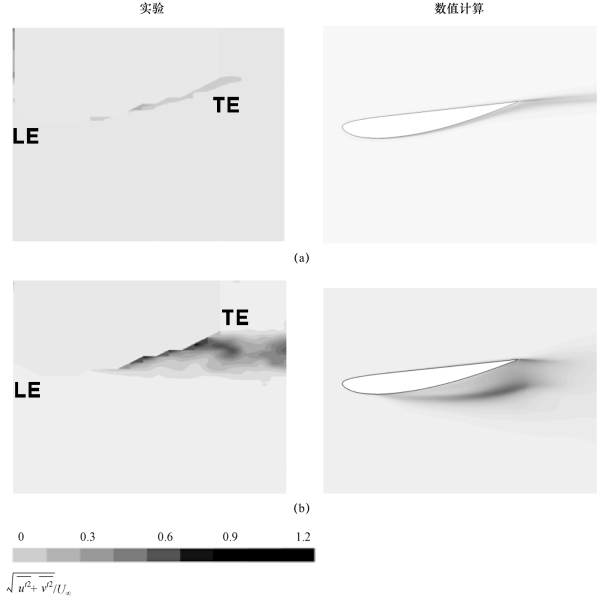
图5-36　水翼吸力面上的时均湍流脉动强度分布（α=8°，Re=7×105）

（a）无空化（σ=2.00）；（b）云状空化（σ=0.80）(www.daowen.com)

当σ=2.00时，湍流脉动分布基本局限于水翼吸力面的近壁区域，空化流场较为稳定；当σ=0.80时，高湍流脉动区域基本集中水翼尾缘处。结合空化流场的流场结构图可以看出，当处于云状空化阶段时，在水翼尾部会出现周期性的大尺度空泡团的脱落现象，空化云的脱落和溃灭导致了水翼尾部流场速度的大范围脉动，由于强烈的汽、液相间的质量和速度交换，形成高湍流脉动区域。

图5-37对比了α=8°、σ=2.00和σ=0.80时，在特征位置处的时均湍流脉动强度统计分布。在计算中，基于湍流模型的封闭模式，可以直接提取湍流动能值k，从而通过表达式间接得到时均湍流脉动强度。由图中可以看出，空化现象导致了流场湍流脉动特性的增加，当σ=0.80时，所形成的湍流边界层较厚。当σ=2.00时，数值计算结果与实验结果有较好的一致性；当σ=0.80时，在空化核心区域内，数值计算预测的湍流脉动强度要略小于实验测量值。这可能是因为现有的计算模型不能反映空穴溃灭对湍流产生的贡献。

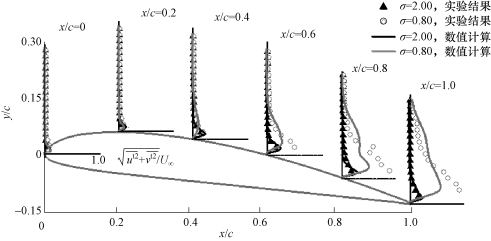
图5-37　时均湍流脉动强度分布（α=8°，Re=7×105）

涡量来源于流场存在的速度梯度，是描述有旋流动的一个运动学物理量。在空化现象中，涉及流动分离、空泡团的脱落等情况，对涡量进行分析具有重要的意义。图5-38给出了在上述不同的工况条件下，水翼周围的时均z向涡量分布，这里，z向涡量定义为

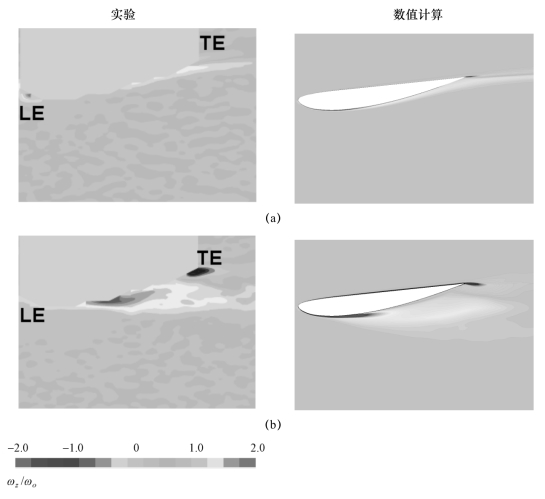
图5-38　水翼吸力面上的时均涡量分布（逆时针方向为正，α=8°，Re=7×105）（见彩插）

（a）无空化（σ=2.00）；（b）云状空化（σ=0.80）

在图5-38中，实验测得的水翼尾缘的湍流边界层厚度。当σ=2.00时，对应于自水翼前后缘开始剪切流所在的位置，出现了两个高涡量聚集区——涡带，上、下涡带的涡量符号相反，说明两处的旋涡方向不同，而其他区域的旋涡特性并不明显，表现为涡量峰值较小。当处于云状空化（σ=0.8）工况时，水翼尾缘处大尺度空泡团的脉动脱落现象导致流场处于不稳定的状态，致使水翼尾缘处的旋涡特性得到发展，上、下涡带随着空化区域的延伸而逐渐向后拉长，涡量聚集区域明显扩大。由此说明，空化产生与旋涡结构之间明显的依赖关系，空化加剧了流场中的质量与速度交换，体现出更为明显的旋涡特性。

图5-39进一步给出特征位置处的时均涡量随距水翼壁面距离y/c的分布。当σ=2.00时，在水翼前缘处，旋涡层较薄，随着x/c的增大，其最大旋涡层厚度在x/c=1.0处，其值约为0.1c；当σ=0.80时，空化现象的产生增加了水翼表面的旋涡区域，其最大旋涡层厚度约为0.3c（x/c=1.0c），并且旋涡强度也明显大于σ=2.00时的测量值，表现为涡量峰值较大。在近壁面处，存在明显的旋涡空化区，涡量随着离翼型壁面垂直距离而变化，在远离壁面区域，涡量趋近于零。结合图5-38，数值计算与实验结果均表明，空泡团的脱离会对湍流空化流场造成相当大的影响，涉及复杂的涡流结构；空化现象扩大了水翼吸力面上的旋涡区域，增强了旋涡强度，使得湍流强度及湍流边界层的厚度有显著的增加。

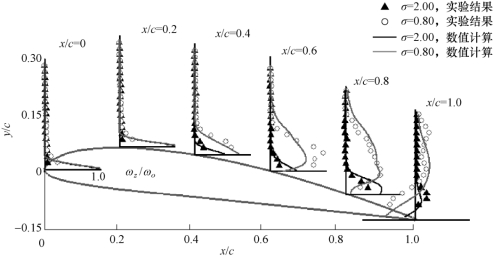
图5-39　时均涡量沿距壁面距离y/c分布（α=8°，Re=7×105）