图5-7给出了云状空化阶段，云状空穴流动形态随时间的准周期性变化过程，实验中分别观察了流场侧视图和仰视图。虽然侧视图与仰视图不是同时拍摄的同一事件，但两事件是在同一次实验中拍摄的，具有基本相同的变化过程。图5-8描述了对应工况下，数值计算得到的非定常空穴以及旋涡结构的发展过程。通过与实验结果对比，数值模拟结果形象地描述了附着型空穴的生长（反向射流的发展）、空穴的断裂的准周期变化过程。在此工况下，云状空化的发展周期约为Tcycle=40 ms（Tcycle为当α=8°和σ=0.80时，云状空化发展的一个完整周期）。为了更清晰地描述云状空穴的旋涡运动，在图5-8中标出了空穴内部流场的流动方向。在t=0.125Tcycle时刻，在水翼前缘处形成透明状附着型空穴，并处于持续的增长状态；在t=0.475Tcycle时刻，附着型空穴逐渐覆盖了水翼的整个吸力面，并开始在空穴尾部产生逆时针的空化旋涡。t=0.625Tcycle～0.875Tcycle阶段，在紧贴壁面的区域内诱导了一股指向上游的反向射流，并持续向上游运动，水翼尾部的水汽混相区域逐渐形成并扩大，而透明状的汽相空穴区域则逐渐缩小。在空穴前缘附近，反向射流与主流相遇，两股方向相反的流动相互作用。在t=1.0 Tcycle时刻，随即产生了空穴的断裂和大尺度空泡的旋涡脱落。图5-9给出了附着型空穴断裂时刻，绕水翼的局部压力场和流场结构。从图中可以看出，由于反向射流与主流的相互作用，在水翼前缘处产生了明显的局部高压，局部高压是引起空穴断裂的主要原因，空穴断裂位置会出现明显的旋涡结构。空穴断裂后，空泡团随主流不断向下游运动。

图5-7　云状空穴准周期性发展过程（σ=0.80，α=8°，Re=7×105）

（a）0.125Tcycle；（b）0.250Tcycle；（c）0.475Tcycle

图5-7　云状空穴准周期性发展过程（σ=0.80，α=8°，Re=7×105）（续）

（d）0.625Tcycle；（e）0.875Tcycle；（f）1.0Tcycle

图5-8　云状空化阶段的空穴形态（σ=0.80，α=8°，Re=7×105）

（a）0.125Tcycle；（b）0.250Tcycle；（c）0.475Tcycle；（d）0.625Tcycle；（e）0.875Tcycle；（f）1.0Tcycle

图5-9　附着型空穴断裂时刻的局部压力场与流场结构（σ=0.80，α=8°，Re=7×105）

（a）压力云图；（b）速度矢量分量

图5-10描述了在一个完整的云状空化的发展周期内，实验观察得到的附着型空穴前缘、尾缘的瞬时和时均的相对位置。从图中可以看出，在空穴的发展过程中，空穴前缘的位置相对比较稳定，而空穴尾缘则处于较大幅度的波动。图5-11描述了在距水翼前缘0.2c、0.4c、0.6c、0.8c、1.0c处的空穴厚度随时间的脉动。水翼中后部的空化云时均厚度要明显大于水翼前缘处的厚度，并呈现大幅度波动，呈现出强烈的非定常变化，空穴厚度脉动的最大幅度发生在0.8c与1.0c位置处。

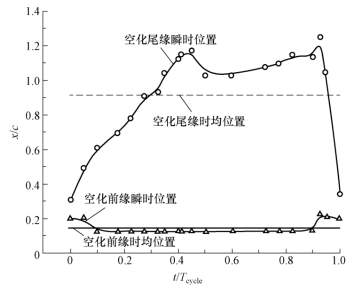
图5-10　空穴前缘与尾缘的瞬时和时均相对位置图（σ=0.80，α=8°，Re=7×105）

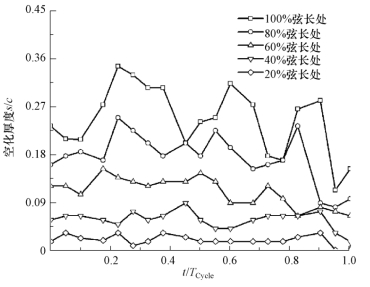
图5-11　不同特征位置处空穴厚度随时间的脉动（σ=0.80，α=8°，Re=7×105）

图5-12给出了采用图像二值处理方法得到的空穴面积变化的过程。图5-13描述了在σ=0.8时，无量纲空穴面积S/Sc（S是空穴面积，Sc是水翼剖面面积）在3个发展周期内的变化曲线。在空穴的非定常发展过程中，空穴面积的最小值接近零，最大值在1.1Sc左右，平均值为0.72Sc，通过图像处理得到的结果和数值计算的结果所描述的空穴面积随时间的变化过程均呈现明显的周期性，也可描述空穴的非定常变化过程。

图5-12　空穴图像二值处理过程

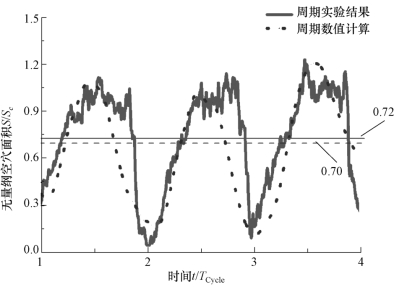
图5-13　附着型空穴面积随时间的波动（σ=0.80，α=8°，Re=7×105）(www.daowen.com)

空穴内部的汽-液两相密度变化也是表征空穴非定常特性的重要指标。空化流动时，汽-液两相呈现明显的当地变化，在附着型空穴区域内，水蒸汽含量的差异将导致图像灰度值的不同。Wonsik等通过对空化图片进行灰度值测量，建立了灰度值与含汽量之间关系的经验公式，用以分析空化的多相流动形态。应用Wonsik的处理方法，表5-1给出了5个特征监测点的灰度值时间序列的统计数据（统计样本为10个云状空化的发展周期），包括时均值（Mean）、最大概率密度值（Mode）、标准差（Standard deviation）。图5-14给出了水翼截面示意图及5个监测点的位置（监测点分别位于x/c=0.2、x/c=0.4、x/c=0.6、x/c=0.8和x/c=1.0位置）。由于实验条件所限，尽管不能定量地给出灰度值与含汽量之间的关系，但对于理解空化流场的非定常特性则有一定的帮助。

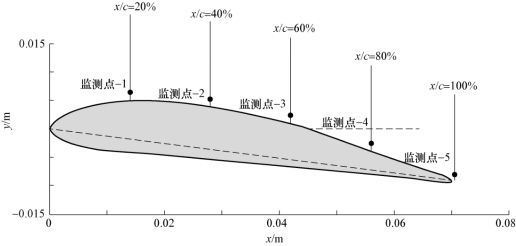
图5-14　水翼剖面示意图及监测点的相对位置

表5-1　监测点位置处灰度值的统计规律（σ=0.80，α=8°，Re=7×105）

图5-15（a）对各个监测点灰度值的瞬时值进行了概率密度函数（Probility Density Function，PDF）分析，数值0对应于黑色区域（无空化区域），数值255对应于像素饱和值，即白色区域（空化区域）。图5-15（b）是相应的局部放大图。结合表5-1和图5-15可以看出，在水翼前缘处（如x/c=0.2位置处），其灰度的时均与标准差值明显小于水翼中、尾缘处，说明该处的灰度值随时间的脉冲振幅相对较小。表明在水翼前缘处，水蒸汽含量较高，往往呈现比较稳定透明状的空穴状态。在水翼中、尾缘处（0.4≤x/c≤1.0），由于此处存在周期性的大尺度空泡团的周期性脱落，其瞬时灰度值谷值与峰值间隔出现，灰度值随时间的波动程度和幅度相对较大，表明在该区域存在大的密度变化，这显然是由于空穴的生长和断裂引起的。

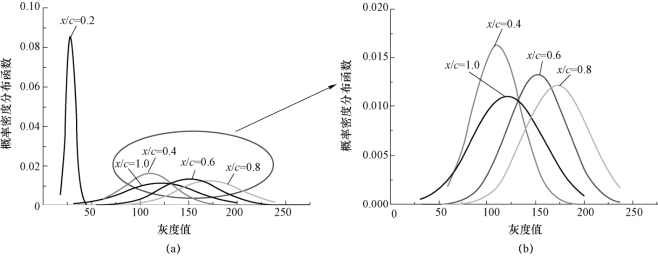
图5-15　监测点灰度值时间序列的PDF分析（σ=0.80，α=8°，Re=7×105）

（a）整体分布；（b）局部放大

为了揭示云状空穴的断裂机理，图5-16分别给出了翼型吸力面的相对高压力系数（研究中，取Cp＞0）和反向射流的时空演变过程，图中纵坐标表示沿弦长方向的长度，横坐标为时间。在附着型空穴的持续增长阶段，空穴与壁面之间的近壁区域并无明显的反向射流产生。当空穴发展到最大时，在翼型尾缘处，如图5-16（a）的1.1Lref～1.5Lref处，会产生明显的相对高压区域。由于逆压梯度的作用，首先在翼型尾缘处产生了如图5-17所示的反向射流，反向射流的初始大小大致在2～3 m/s。在反向射流向水翼前缘的发展过程中，不同时刻水翼表面都会产生一个局部高压区域，并且逆压梯度的持续作用使反向射流有逐渐增大的趋势，大致维持在4～6 m/s。

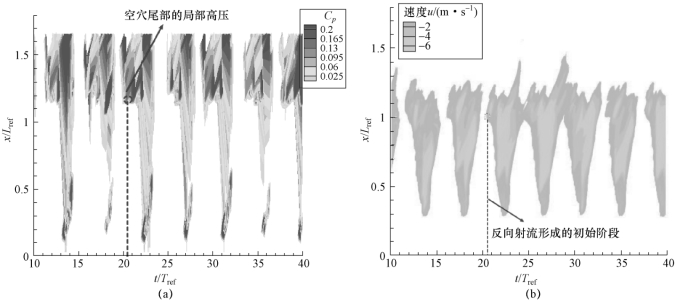
图5-16　高压力系数、反向射流随时间的演变过程（σ=0.80，α=8°，Re=7×105）

（a）高压力系数；（b）反向射流

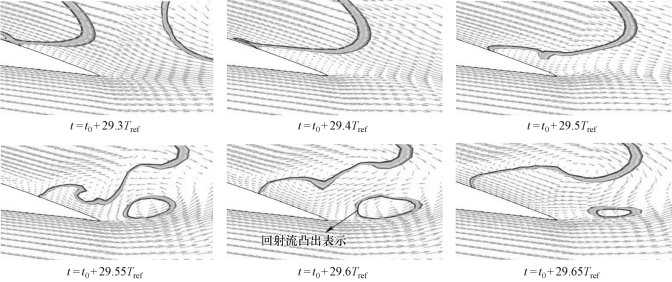
图5-17　反向射流的形成与发展过程（σ=0.80，α=8°，Re=7×105）

图5-18描述了在反向射流的形成与发展的初始阶段，水翼尾缘处的压力系数和速度在典型时刻的分布。从图5-18可以看出，在t=t0+29.5Tref～t0+29.65Tref时刻，水翼尾缘处的逆压梯度陡增，诱导了反向射流的发生，引起反向射流的主要因素是近壁的旋涡运动而引起的逆压梯度。该逆压梯度持续作用使反向射流获得足够的能量不断向水翼前缘发展，直至在水翼前缘处切断整个附着型空穴。

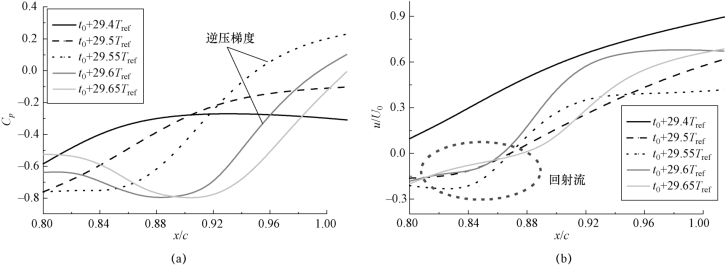
图5-18　空穴尾缘的压力系数和速度分布（σ=0.80，α=8°，Re=7×105）

（a）压力系数；（b）沿主流方向的速度

为了更为深刻地理解在非定常发展过程中，空穴形态、反向射流和空化旋涡结构等多物理变量之间的关系，图5-19（a）分别给出了翼型尾缘附近（x/c=0.9）处，无量纲速度u/U∞、翼型尾缘处的压力系数Cp和涡量在大约4个周期时间内随时间的变化趋势；图5-19（b）给出了对应时刻的空穴形态示意图。具体对A、B、C 3个典型阶段的流场结构进行了分析，A为前一周期的空泡脱落过程，B为后一周期附着型空穴的持续增长过程，C为后一周期反向射流发展阶段。从图中可以看出，伴随着前一周期空泡的脱落，在A阶段，翼型尾缘处的旋涡结构得以加强，而反向射流逐渐减弱，当附着型空穴进入其后的持续增长阶段B时，由于此时翼型尾缘处的压力较小，没有反向射流现象的发生，此时该处的旋涡结构并不明显，体现为涡量峰值较低。当附着在翼型上的空穴增长到最大后，在翼型尾缘处出现了高压力区域，反向射流现象开始出现，伴随着高压力区域长时间的持续存在，反向射流逐渐增强。当反向射流到达翼型前缘，附着型空穴开始断裂，大尺度的脱落空泡团初步形成，随即完成空穴的周期性发展过程。

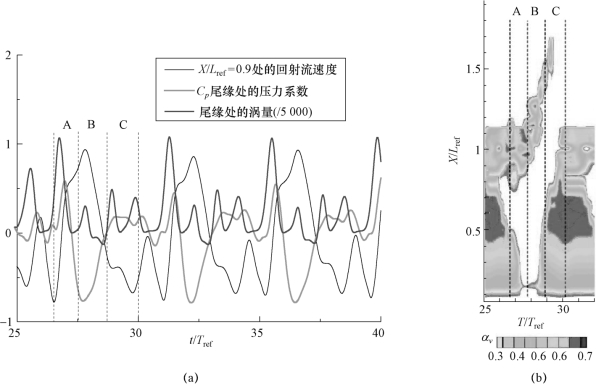
图5-19　翼型尾缘处的速度、压力系数和涡量随时间的变化趋势（σ=0.80，α=8°，Re=7×105）

（a）速度、压力和涡量分布；（b）空穴形态分布