在上述内容中，对Kubota和IDM空化模型进行了基本的介绍，相关数值计算结果表明，上述两种不同空化模型对于非定常空化流场的不同区域，如附着型空穴区、空泡分离区以及空穴的闭合端的预测有着明显的差异。IDM空化模型基于交界面质量和动量守恒所推导，对低汽相体积分数的混相区域逐渐过渡到高汽相体积分数的纯汽相区域的动态交界面有很好的表现，可清晰模拟出附着型空穴中，不同含汽量区域的空穴界面。Kubota模型基于空泡动力学理论，对空穴的断裂以及大尺度空化泡旋涡脱落等非定常特征有较好的描述。下面将重点介绍一种基于混合密度分域的空化模型（Density modify based cavitation model，DMBM）。与前面介绍的混合湍流模型（FBDCM）的构建思想类似，在含汽量比较大的翼型前缘附着纯汽相及过渡区域内，采用IDM空化模型，以模拟空穴内部、清晰的水汽界面及其反向推进的过程；在含汽量比较小的空化混相脉动区域内，采用Kubota模型，以捕捉空泡团的旋涡脱落现象。其具体的表达式为

在基于混合密度分域的空化模型构建中，依然借助函数χ（ρm/ρl）对空化流场进行分域处理，模型参数C1、C2、C3和C4的取值，可影响混合空化模型中的Kubota模型和IDM空化模型在混相介质中的过渡区间和作用区域。按照3.3节的分析思路，利用基于代理模型（Surrogate-based analysis and optimization）的无量纲整体敏感性分析方法对该模型的分域函数χ（ρm/ρl）进行分析，将C1、C2、C3和C4作为模型评价的自变量，自变量初步取值范围如表4-7所示。代理模型的分析目标依然定义为云状空化（σ=0.80，α=8°，Re=7×105）工况下，水翼的时均升力系数Cl和动力特征频率f实验值与数值预测值之差Cl_diff和f_diff。

表4-7　不同空化模型预测得到的水翼升力系数的时均值和特征频率

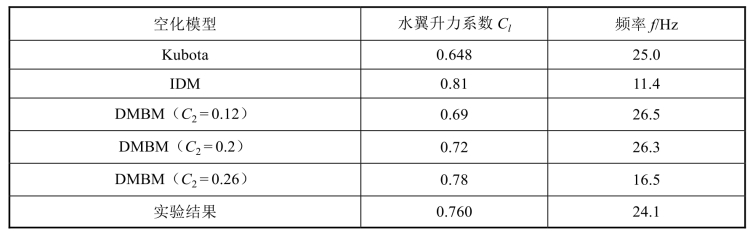
图4-38给出了对于DMBM，自变量对目标变量的总体敏感度指标分布。与3.3节中对于FBDCM湍流模型的分析结果相似，目标函数对各自变量的敏感程度分布趋势基本一致，由大到小依次为C2、C3、C4、C1，说明模型预测精度主要受到经验系数C2的影响。值得注意的是，与FBDCM湍流模型相比，DMBM中对于C2的敏感程度更为显著。由前面的分析可知，C2主要调节Kubota模型和IDM空化模型在模型中的影响比重，水翼的水动力特性直接与空穴的断裂和非定常空泡的脱落细节相关，然而Kubota模型和IDM空化模型对上述流动细节的描述存在显著的差异。因此，在DMBM中，数值计算结果对于C2的敏感程度更为突出。根据自变量的初步优化结果，选取C1=4、C3=0.6和C4=0.2。通过提取最优解可缩小自变量C2的取值范围（C2=0.12～0.26）。综合比较数值计算结果与实验结果，采用C2=0.2的计算结果与实验值最为接近。

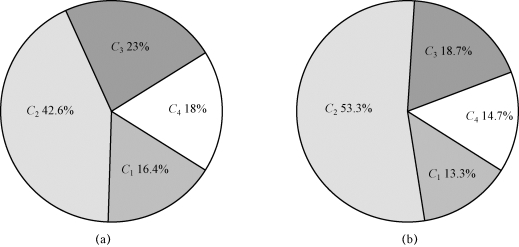
图4-38　总体敏感度分析饼图

（a）Cl_diff；（b）f_diff

图4-39分别给出了Kubota、IDM和DMBM（C2=0.2）空化模型预测得到的非定常空穴形态与实验结果的对比，结合附着在翼型上的空穴长度随时间的变化过程（如图4-40所示）可以看出，采用Kubota空化模型过早预测了空穴的断裂，这是由于Kubota空化模型根据R-P方程计算单一气泡体积的扩散速度，假设空泡是均匀的径向发展且不会相互作用。附着型空穴的发展和回缩、断裂过程可以视为无数空泡体积变化的整体行为，对空穴内部的流场结构的特征差异不能很好地体现，而采用IDM空化模型所预测的附着型空穴长度则一直比较稳定。比较而言，DMBM空化模型对空穴发展的两个典型阶段均有比较客观的描述，该模型结合了IDM与Kubota空化模型在模拟云状空化流动现象的优点，准确地模拟出附着在翼型前端稳定的水汽含量相对较大的空穴与翼型尾部水汽含量相对较低的不稳定的汽-液两相区，两者动态界面非常明显。此外，DMBM空化模型合理地预测了空泡脱落时刻翼型尾部的不稳定脉动区，当反向射流发展到水翼前缘位置时，会切断附着型空穴，导致空穴长度的骤降，这与实验观察有较好的一致性。

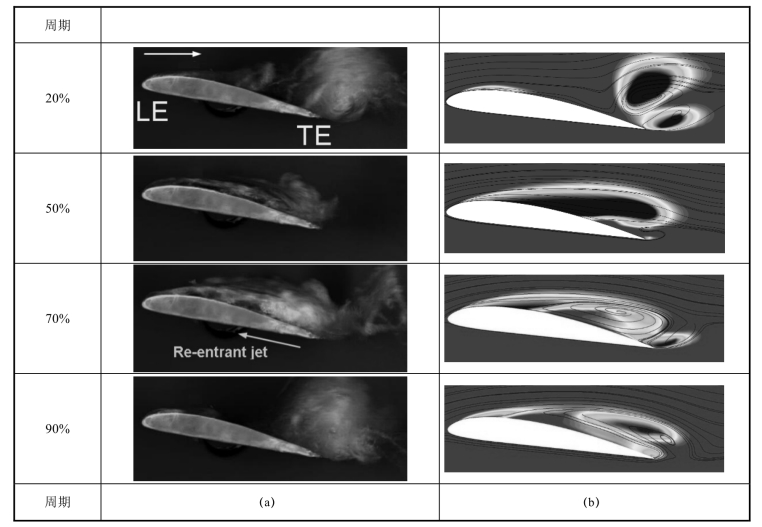
图4-39　不同空化模型预测得到的空穴形态云图随时间的变化过程（σ=0.80，α=8°，Re=7×105）（见彩插）

（a）实验结果；（b）Kubota模型

(www.daowen.com)

图4-39　不同空化模型预测得到的空穴形态云图随时间的变化过程（σ=0.80，α=8°，Re=7×105）（续）（见彩插）

（c）IDM；（d）DMBM

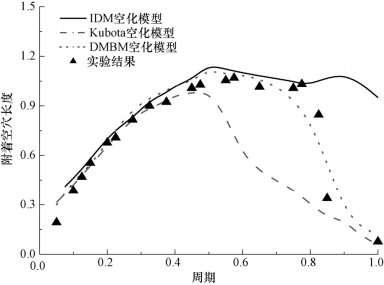
图4-40　不同的空化模型预测得到的附着型空穴长度随时间的变化过程（σ=0.80，α=8°，Re=7×105）

结合采用Kubota、IDM和DMBM空化模型得到的时均升力系数及特征频率（表4-7）可以看出，采用IDM空化模型得到的升力频率与实验测量值有较大的出入，其值远小于实验值，而采用Kubota和DMBM空化模型预测的比较接近，与实验测量值差别不大。为了更好地说明空化模型对预测非定常空化流场结构及其周期演化规律的差异，图4-41描述了采用IDM和DMBM空化模型得到的云状空化状态下，水汽含量随时空的变化云图。IDM空化模型在预测空穴断裂及空化云的脱落方面有着明显的缺陷，过度预测了空穴的附着行为，导致云状空穴的发展周期过长，这也就解释了其时均升力系数过大的原因。与Kubota空化模型类似，DMBM空化模型均合理地预测了云状空化周期性的演化规律及大尺度空泡的脱落现象。两者预测的动力特征频率基本一致。这是由于在云状空化中，反向射流的产生和发展会直接导致附着型空穴的断裂和空泡团的脱落现象，而反向射流往往是水汽混相介质，对于分域模型DMBM空化模型，在这部分区域内，Kubota空化模型将起到主导作用。

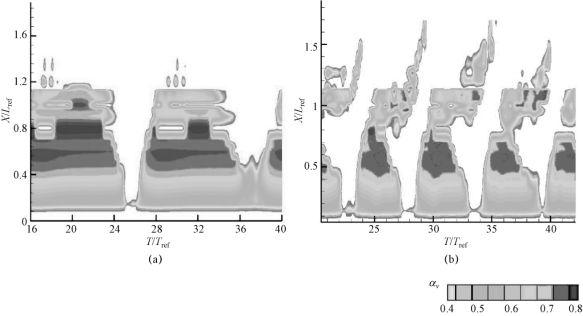
图4-41　不同空化模型预测得到的云状空化状态下，水汽含量随时空变化云图（σ=0.80，α=8°，Re=7×105）

（a）IDM模型；（b）DMBM模型

图4-42给出了应用不同空化模型预测得到的时均沿主流方向的速度u在特征剖面x/c为0.4、0.6、1.0和1.2上的分布。Kubota、IDM和DMBM空化模型在预测空化流场结构的差异决定了时均速度分布的差异：IDM空化模型过度预测了空穴完整的发展周期，在相同的计算时间内，附着型空穴生成、持续发展到水翼尾缘这一过程的预测次数较少，而在这一个过程中，速度较大的主流流动往往对空穴内部的速度分布起到主要作用。因此，当对速度值做时间平均统计时，在x/c=0.4和x/c=0.6处，IDM空化模型预测得到的近壁区域速度绝对值较小。值得注意的是，在水翼近壁区域，由于空化现象易产生，水汽含量较大，此时DMBM空化模型中IDM空化模式将起到主导作用，所以DMBM空化模型预测得到的在近壁区域内的速度曲线的变化趋势与IDM空化模型更为接近，与实验测量值吻合较好。另外，在水翼尾缘处（x/c=1.0和x/c=1.2），不同空化模型预测结果差异不大。

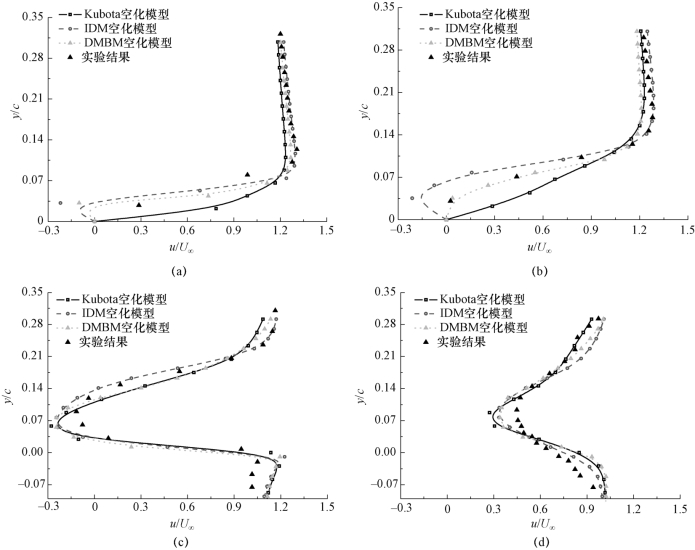
图4-42　不同空化模型预测得到的特征剖面处，沿主流方向的速度分布与实验结果的对比（σ=0.80，α=8°，Re=7×105）

（a）x/c=0.4；（b）x/c=0.6；（c）x/c=1.0；（d）x/c=1.2

综上所述，通过比较不同湍流模式和空化模型在空化流动的适用性，发现不同模型对于非定常空穴形态及流场结构模拟结果的差异反映了其所体现的物理机制是不同的。结合非定常空化流动特性，基于实验结果进行模化分析，最后介绍了一种基于混合密度分域的非定常空化流动的数学方法，提高了对非定常空化流动的预测精度，更清晰地模拟了空化区域的两相流动结构，精确地预测了非定常空穴长度的变化趋势和水动力特性。