基于汽-液相间传输的空化模型（TEM）通过添加合适的源项，对质量或体积分数采用传输方程来控制汽-液两相之间的质量传输过程。目前常用的基于质量传输的空化模型中，忽略热传输和非平衡相变效应，采用组分传输方法来描述液相体积含量的输运方程为

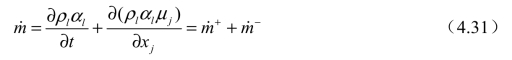
在空化现象的数值模拟中，当流场中某处的压力低于饱和蒸汽压pv时，存在使液体蒸发的势，其大小可以通过源项来表示，代表了该点处在单位时间内从单位体积中蒸发的液体质量。当流场中某处的压力高于饱和蒸汽压pv时，代表了该点处在单位时间内从单位体积中凝结的汽体质量。基于不同模型的构建方法，此类方法衍生出多种不同的传输模型。在后续分析中，将重点研究常用且理论推导比较完善的TEM空化模型中，蒸发与凝结源项的不同表征对空穴发展及空泡脱落过程模拟的影响。

4.5.2.1　基于空泡动力学方程的质量传输模型

基于空泡动力学方程的空化模型根据Rayleigh-Plesset（R-P）方程计算单一空泡体积的扩散速度。根据单个球形空泡的R-P方程，空化相变主要由泡内压力pv与泡外液体压力p∞之差控制：

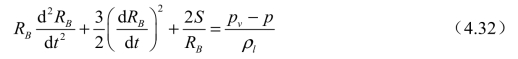
式中，RB为空泡直径；pv为泡内压强（假设为液体温度下的蒸汽压）；p为液体压强；S为表面张力系数。

假设空泡是均匀的径向发展且不会相互作用，忽略二次项和表面张力项，则式（4.32）简化为

式中，正负号（±）可由空泡内外压力差来判断，若是压力小于蒸汽压，表示正在进行汽化蒸发过程，将取正号，反之亦然。

汽相体积百分比αv可由空泡体积和空泡数密度NB判断，即

假设空泡数密度在流场中为固定值，则每单位总的相间质量传输率为

上式即为空泡动力学模型基本推导过程。图4-31给出了基于球型空泡的R-P方程表征的空化蒸发与凝结过程。在基于R-P方程的质量传输空化模型中，往往需要再给定空泡的初始体积分数和空泡数密度才能进行运算，不同数值的选取也有可能影响模拟结果的准确度。下面，简要给出了基于上述方法推导而来的两种常用的空化模型。

图4-31　基于球型空泡的R-P方程表征的空化蒸发与凝结过程

（a）凝结；（b）蒸发

1.Kubota空化模型

Kubota空化模型结合泡间两相流动理论，认为空穴内外为连续体，空穴为一密度剧烈变化的可压缩性黏性流体，重点考虑了空化生长和溃灭时空泡体积变化的影响，适于模拟空化的非定常过程。在该模型中，单位体积内的相间传输速率分别为

由式（4.36）和式（4.37）可知，汽-液相间的质量传输速率与泡内压力pv与泡外压力p之差的平方根成正比。计算中，相关的经验系数设定为：αnuc=5×10-4，RB=1×10-6m，Ck_dest=50，Ck_prod=0.01。

2.Singhal空化模型

Singhal空化模型也是基于R-P方程推导而来，其通过假设来流中存在单位体积密度为n的汽核，推导出了密度随时间的变化率与蒸汽分数αv、气泡半径变化率dR/dt、平均气泡大小等物理量之间的关系。Singhal空化模型充分考虑了以下因素：①　汽-液相间的交互作用；②　速度的湍流脉动。

单位体积内的相间传输速率分别为

如式（4.38）和式（4.39）所示，在Singhal模型中，当地湍流动能对蒸发与凝结源项的大小有直接关系。

上面给出的两种常用的基于R-P方程的质量传输空化模型，蒸发与凝结项的不同表征对空化流场的预测有着重要的影响。下面，以绕NACA66附着型片状空化流动（σ=1.49，Re=750，000，U∞=5 m/s，α=6°）为例，研究了Kubota和Singhal空化模型对于空化流动预测结果的影响。

图4-32给出了不同空化模型得到水翼表面的时均压力系数及其波动值分布与实验结果的对比。图中，x表示从前驻点开始沿水翼表面到取值点的弧长，c表示水翼的弦长。通过计算与实验结果的对比可以看出，水翼表面的压力系数分布均呈以下规律：由驻点最大值急剧下降，当到达斜面分离涡区时，压力系数下降到负压最大值并逐渐趋于稳定，这是由于当地压力低于液面汽化压力时，会出现肩空泡，在水翼前缘处，定压值-Cp对应于附着空化区域，此时，压力系数的波动值较小。压力系数曲线经过一段稳定过渡逐步上升而后达到一个稳定区，而在空穴尾部闭合区域内，由于流场结构较为复杂，压力波动值增大。

图4-32　不同空化模型预测得到的绕水翼的时均压力系数和其波动值（σ=1.49，α=6°，Re=7.5×105）

图4-33进一步给出了不同空化模型预测得到的典型空穴形态及对应时刻的的蒸发与凝结源项云图。从图中可以看出，蒸发源项主要集中于低密度的附着型空化区域；凝结源项集中于空穴界面和空穴尾部的闭合区域内。不同空化模型所表征的蒸发与凝结项的作用区域存在明显的差异。通过比较不同空化模型计算结果与实验值的区别，可以看出在Singhal模型的数学构建中，考虑到了湍流动能k对相间传输过程的影响，对于空化的蒸发与凝结过程存在非线性反馈作用，空化相变过程与湍流流场结构之间的耦合作用增强，导致了所预测得到的空化流场的非定常特性更为显著，在水翼后部，也存在明显的压力脉动。另外，应用Singhal空化模型得到的时均附着型空穴长度明显小于实验测量值，而Kubota模型的预测结果与实验结果吻合较好。

图4-33　不同空化模型预测得到的空穴形态、蒸发与凝结源项云图（σ=1.49，α=6°，Re=7.5×105）（见彩插）(www.daowen.com)

（a）空穴形态；（b）蒸发源项；（c）凝结源项

4.5.2.2　基于界面动力学的质量传输模型

近年来，研究者广泛采用基于R-P方程的空化模型对空化流场进行研究，这种形式的空化模型均涉及蒸发与凝结源项的经验常数，并且模型的经验系数取值并不相同。换言之，上述模型的经验系数对模型的通用性有一定的限制。Senocak和Shyy从空泡界面动力学的运动机理着手，不再从传统上的R-P方程着手来推导汽-液相间的蒸发与凝结源项，而是从空泡界面动力学出发来推导汽-液相间的质量传输速率，由此形成了基于界面动力学的质量传输模型（Interfacial Dynamic Model，IDM）。

如图4-34（a）所示，假设在汽相与液相之间存在空泡界面，在该界面上质量连续方程和动量平衡方程、N-S方程可以写为

图4-34　均相流中的空泡界面及汽-液两相界面示意图

（a）空泡界面；（b）汽-液两相界面

图4-34（b）给出了基于均匀流理论的汽-液两相界面示意图，其中混合密度可以定义为

如果忽略表面张力与黏度的影响，上述方程可以简化为

由式（4.43）可以得到

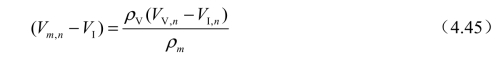
而式（4.44）可写为

基于混合相密度，联立式（4.43）和式（4.46），有

基于上述分析，相间质量传输方程可以写为

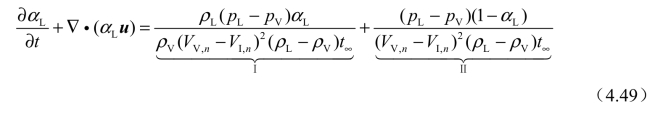
当环境压力降低到当地饱和蒸汽压时，会发生空化现象，由式（4.49）可以看出，在液相中（αL=1），式（4.49）的第Ⅱ项为零，所以应该在式（4.49）第Ⅰ项的压力项中引入min函数，在凝结源项式（4.49）第Ⅱ项中引入max函数，空化模型表达式为

汽相沿界面的法向速度由汽相含量的梯度导出：

在计算中，假设交界面法向速度VI，n与VV，n成比例关系。IDM空化模型与现有空化模型都是基于相间传输方程的，其主要区别在于：IDM空化模型基于空泡界面动力学理论，对于空化现象，假设其有一个清楚的交界面，也就是存在较强的相变化趋势，并假设相变化发生于混合相和汽态相。在相间质量传输速率的推导过程中，主要考虑了基于时间变化的空泡界面速率与汽-液相在空穴界面的法向运动速度之间的关系，其中空穴界面由不同位置处的体积分数确定。理论上，空化模型中消除了经验系数对空化模型的影响，IDM空化模型具有更普遍的适用性，并且IDM对于附着型定常片状空化流动已取得良好的应用效果。

通过上面的分析，可以看出，不同空化模型在构建过程中，所希望表达的物理内涵存在一定的差异。下面将以典型的基于空泡动力学（Kubota空化模型和基于相间界面动力学）IDM空化模型为例，分析不同相间质量传输空化模型对绕Clark-Y型水翼的非定常云状空化（σ=0.80）流场计算的影响。

图4-35描述了不同空化模型预测得到的附着型空穴长度随时间的变化过程，结合在反向射流发展阶段中空穴形态的差异（图4-36），两种空化模型的差异主要体现在反向射流发展、附着型空穴断裂和空泡脱落阶段。Kubota空化模型对于大尺度空泡团的旋涡脱落现象有较好的体现，但其过早预测了空穴的断裂。IDM的主要优势在于该模型准确地模拟出附着型空穴内部流场结构的差异，当空穴发展至最大几何尺度后，空穴尾部存在明显的反向射流现象。该模型较好地预测了空化区域内纯汽相区与两相混合区之间的界面，并且界面随时间变化的非定常特征得以展示，这一点与实验结果基本相符。但是，通过分析附着型空穴长度随时间的变化趋势，可以观察到，采用IDM空化模型所预测的附着在水翼上的空穴长度在该过程中一直比较稳定，不会出现如实验观察得到的由于反向射流导致的附着型空穴突然减小的现象。换言之，IDM空化模型对云状空化阶段，空穴的断裂及大尺度空泡团脱落现象的预测能力存在明显的不足。

图4-35　Kubota模型和IDM空化模型预测得到的附着型空穴长度随时间的变化过程（σ=0.80，α=8°，Re=7×105）

图4-36　在反向射流发展阶段，Kubota模型和IDM空化模型预测得到的空穴形态云图随时间的变化过程（σ=0.80，α=8°，Re=7×105）（见彩插）

（a）Kubota模型；（b）IDM空化模型

为了解释Kubota模型和IDM空化模型在模拟空化流动现象，特别是空泡团旋涡脱落现象的差异，图4-37给出了云状空化周期性发展的后期，应用不同空化模型预测得到的凝结源项比值云图随时间的变化。从图中可以看出，由于Kubota模型模拟得到的凝结速率要明显大于IDM空化模型，尤其是在附着型空穴的闭合区域内，所以Kubota模型对于预测空穴的断裂及空泡脱落等液化凝结过程更为明显。

图4-37　在反向射流发展阶段，Kubota模型和IDM空化模型预测得到的凝结源项比值随时间的变化过程（σ=0.80，α=8°，Re=7×105）（见彩插）