在基于正压流体状态方程的空化计算方法中，混合物的密度由状态方程确定，即密度是压力与温度的函数。该模型采用均相流体模式计算两相空化流动，并假设与流动的特征时间尺度相比，蒸发和凝聚过程可以看成是瞬间完成的。流体密度是压力的单值函数，因此可将流体密度与压力之间的关系表示为ρm＝ρm（p），该函数可用分段函数表示，定义变量　Δpv：

式中，ρl、ρv分别为液相和汽相的密度；cmin为流场中的最小声速。

根据下面的物理假设关系，图4-28给出了流体密度与当地压力之间的关系曲线。

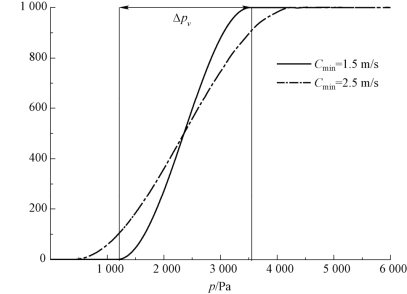
图4-28　流体密度与当地压力之间的关系曲线

采用基于正压关系的空化计算方法模拟了绕圆头回转体的定常空化流动，图4-29给出了σ=0.30，Re=1.36×105时，绕圆头回转体的压力与密度分布云图。图4-30给出了在此工况下圆头回转体表面的压力分布计算结果与Rouse和McNown实验结果的对比，图中横坐标为模型表面位置的量纲归一化参量（其中S表示从前驻点开始沿回转体表面到取值点的弧长，d表示回转体的直径），纵坐标为压力系数。总体而言，计算结果与实验压力分布值比较吻合，实验与数值计算结果有较好的一致性。从密度分布曲线可以看出，在回转体肩部的空化核心区域内，密度较低，而在空穴尾部的闭合区域内，密度值逐渐增大。

(www.daowen.com)

图4-29　基于正压流体状态方程的空化模型预测得到的回转体表面的压力与密度云图（σ=0.3，ReD=1.36×105）（见彩插）

（a）压力分布；（b）密度分布

图4-30　基于正压流体状态方程的空化模型预测得到的回转体的压力与密度分布（σ=0.3，ReD=1.36×105）

（a）压力分布；（b）密度分布

从上述的模拟结果来看，尽管基于正压关系的空化流计算方法可以较好地模拟稳定的附着型空穴，其预测的基本物理量（压力等）与实验结果也吻合较好。Katz等的实验结果表明，在非定常空化流动中，涡的产生和旋涡运动是空化流动的重要特性，特别是在空泡尾部的空穴闭合区域内。对于多相流体，涡量的输运方程为

式中，ω和u分别为流场中的涡量和速度矢量；∂ω/∂t为涡量的当地变化率（rate of change ofvorticity at a fixed point），其物理意义为固定点上的涡量随时间的变化率；为旋涡的对流/变形项（convection and vortex-strentching/tilting term）；为由于不平行的压力和密度梯度导致的斜压矩生成项（baroclinic torque）；为涡量的耗散项（laminar and turbulent diffusion of vorticity）。

很明显，若采用正压流体法则，其密度仅是压力p的函数　，则密度和压力项具有相同的变化梯度，斜压矩　。这就是说，使用正压流体方程无法捕捉到空化流动中斜压矩的产生。在实际上，流场中的压力和密度的梯度并不总是平行的，尤其是在空穴界面及闭合区域内。从理论上讲，基于正压关系的计算方法对预测空化的对流和输运现象存在明显的缺陷。