不同的模型对于空化流动预测能力的差异反映了模型本身所体现的物理机制是不同的。前面考虑到非定常空化流动的特点，分别评价了基于标准k-ε模型的滤波尺度的修正方式（FBM）和密度修正方式（DCM），尽管FBM和DCM在一定范围内均能降低流场中的湍流黏度。但是，两种模型的物理内涵存在明显的差异：对于非定常空化流动，空穴尾部流场存在大尺度的旋涡运动，随着速度梯度的增加，湍流动能迅速变大。FBM没有考虑空化多相流动特性的影响，主要对远离壁面，水蒸汽含量较高的空化云旋涡脉动区域进行滤波修正，以捕捉大尺度涡流所造成的非定常特性，而DCM主要通过对空化区域的混合密度进行修正，影响范围主要集中在近壁空化核心区域内，以考虑汽液混相的压缩性。在远离壁面区域，由于无明显的空化现象产生，其作用效果欠佳。通过上述分析，FBM和DCM的作用区域存在明显的差异，两者分别顾及了不同区域的流动特性。

如图4-18所示，通过实验观察，可以充分了解到非定常云状空穴在其演化过程中所呈现的特征结构：在附着在翼型上（近壁区域）的空穴内部，呈透明状态的汽相区域，必须充分考虑汽-液两相流动的可压缩特性；在翼型尾缘处（远离壁面）的雾状混相区域，包含多尺度涡团脱落的湍流信息。上述非定常空化流动的特征结构在众多实验研究中被普遍证实。基于上述认识，针对FBM和DCM在空化流动模拟应用中的特点，对空化流场基于混合密度的分布进行分域。在不同区域采用不同的湍流黏度修正方式，形成一种基于混合密度分域的湍流模式（Filter-Based Density Correction Model，FBDCM），充分发挥FBM和DCM的优势，以捕捉湍流和空化之间的交互作用和动态行为：在翼型前缘含汽量较大的区域，应用DCM，以体现附着型空穴的可压缩特性；在翼型尾部含汽量较大的雾状空泡团区域，应用FBM，以捕捉大尺度的空泡涡团结构。为了保证湍流黏度的光滑过渡，两种湍流黏度通过下面的混合函数进行桥接，表达形式为

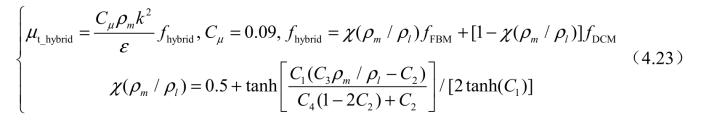
图4-18　云状空化阶段，空穴形态的发展过程（σ=0.80，α=8°，Re=7×105）

在混合密度的分域函数χ（ρm/ρl）中，通过调节C1、C2、C3和C4的取值，可影响混合模型（FBDCM）中的FBM和DCM在混相介质中的过渡区间和作用区域。分域函数χ（ρm/ρl）对于空化流场的调节作用对上述4个经验系数（C1、C2、C3和C4）的取值存在较大的依赖性，目前还难以通过对实验数据的模化来确定不同空化流场特征区域的过渡区间。

下面，将结合非定常云状空化的实验结果，利用基于代理模型（Surrogate-based analysis and optimization）的无量纲整体敏感性分析方法对FBDCM的分域函数χ（ρm/ρl）进行分析。从而获得影响预测精确度的主要因素，并基于分析结果对模型参数进行优化，以期给出能够获得精确预测结果的模型参数。基于前面的研究分析，在混合湍流模型FBDCM中，其滤波尺度选为1.05Δgrid，maxo，Δgrid，maxo为水翼周围O形格的最大尺度，混相指数n取值为10。

采用代理模型进行分析的关键在于建立一个足够精度的近似数学模型。在研究中，主要在于说明分域函数χ（ρm/ρl）中相关经验系数的扰动对空化流场，进而对水动力特性预测精确度的影响。因此，将C1、C2、C3和C4作为模型评价的自变量。为实现分域函数χ（ρm/ρl）在混相介质区间内的合理过渡，自变量初步取值范围如表4-2所示。代理模型的分析目标定义为云状空化（σ=0.80，α=8°，Re=7×105）工况下，水翼的时均升力系数Cl和由空泡团脱落引起的动力特征频率f实验值与数值预测值之差为Cl_diff和f_diff。

表4-2　自变量的初步取值范围

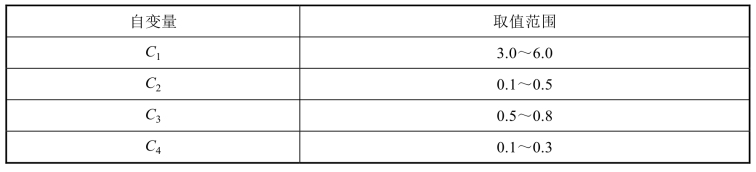
结合面心立方法（FCCD）和拉丁超立方法（LHS），在自变量空间内共生成70个样本点，然后对各样本点进行数值实验，根据数值实验结果，在标准化的变量空间分别采用多项式响应面方法（PRS）、Kriging方法（KRG）、辐射神经元网络方法（RBNN）以及加权平均值近似方法（WAS）建立目标函数与自变量之间的近似关系，并采用一阶交叉验证方法对不同代理模型进行评价，选取PRESS（Predition Error Sum of Squares）作为评价指标，其表达式为

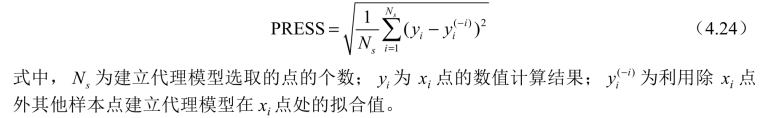
表4-3给出了由不同代理模型拟合得到的误差情况。综合4种模型拟合结果可以看出，WAS模型拟合效果优于其他模型，PRS模型和KRG模型次之，RBNN模型拟合效果最差。因此，选择WAS模型的拟合结果对目标变量做进一步分析。利用WAS模型对绕Clark-Y型水翼的云状空化流动的计算情况进行拟合，通过比较自变量的偏方差和总方差，从而获得各自变量对目标变量Cl_diff和f_diff的相对重要程度。为了综合考虑自变量的局部敏感度和其他自变量对其的相互作用，采用的全局敏感度的定义为

式中，Vi表示单个自变量的偏方差；Viz表示多个自变量组合的偏方差；总方差V=ΣVi+Vij+…+V1，2，…，N。

式（4.25）表示全局敏感度，综合考虑了自变量的局部敏感度和其他自变量对其的相互作用。

表4-3　不同代理模型拟合误差分布

图4-19给出了自变量对目标变量的总体敏感度指标分布。在对目标变量Cl_diff和f_diff的敏感度分析中，各自变量敏感程度分布趋势基本一致，由大到小依次为C2、C3、C4、C1，说明模型预测精度主要受到经验系数C2的影响。

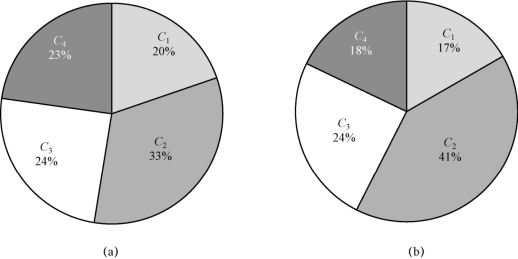
图4-19　总体敏感度分析饼状图

（a）Cl_diff；（b）f_diff

考虑到自变量间相互作用对敏感性分析结果的影响，通过目标变量的变化趋势进一步分析其敏感程度，给出目标变量随自变量C1、C2的变化情况。从图4-20（a）和（b）中可以看出，目标变量f_diff和Cl_diff沿Y轴方向随C2的增加分别有减小和增大的趋势，而沿X轴方向随着C1的增大，变化趋势不明显，且f_diff的变化范围较Cl_diff大，说明目标变量Cl_diff和f_diff均对C2的变化较敏感，且相对其他自变量，C2对f_diff的影响程度较对Cl_diff的影响程度大，这与图4-19所描述敏感度分布情况一致。

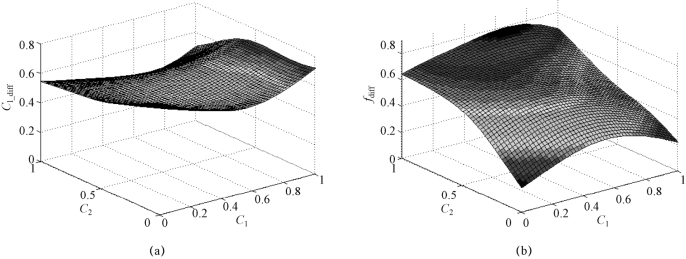
图4-20　目标变量随自变量的变化趋势图

（a）Cl_diff；（b）f_diff

为了更直观地体现与自变量空间相对应的目标函数分布情况，在自变量空间中随机生成均匀分布的104个点，WAS模型的拟合结果在目标空间的分布如图4-21所示。图中红色区域为最优解，即Cl_diff和f_diff同时取最小值。由于设计变量与目标函数是一一对应的，因此由最优解可缩小自变量的取值范围，从而实现对设计空间的优化。表4-4给出了自变量取值范围的优化结果。

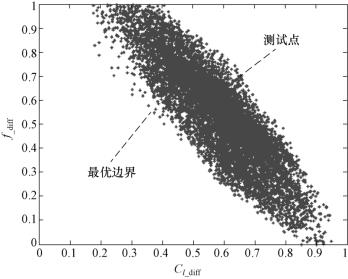
图4-21　目标变量分布图（见彩插）(www.daowen.com)

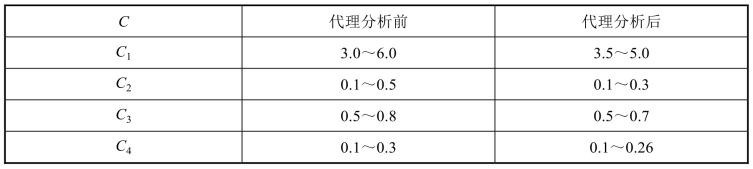
表4-4　自变量取值范围初步优化分析

由上述分析可知，在当前计算工况下，模型参数C2对模型预测精度的影响最大，其他参数在敏感度分析中仅起到参考作用，而非作为优化参数。根据自变量的初步分析结果，选取C1=4、C3=0.6和C4=0.2。其中，χ（ρm/ρl）是在基于混合密度的分域函数，在该模型中，通过C2调节混合模型（FBDCM）中的FBM和DCM的影响比重，图4-22给出采用不同C2值（C2为0.1、0.2和0.3）下，混合函数（χ（ρm/ρl））的分布图。如图4-22所示，当χ（ρm/ρl）较小时，此时采用密度函数的修正方式（DCM），当χ（ρm/ρl）较大时，此时对湍流黏度采用空间滤波的修正方式（FBM）。

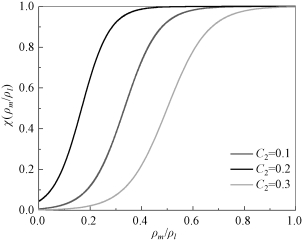
图4-22　不同C2值下，混合函数分布示意图

表4-5综合给出了上述几种基于标准k-ε模型修正的表达方式，包括基于空间滤波的滤波器模型（FBM）、密度修正方式（DCM）和基于混合密度分域的湍流模型（FBDCM）。下面，将综合运用上述几种湍流模型对绕水翼的非定常云状空化发展过程进行模拟分析。

表4-5　不同湍流模型的修正方式

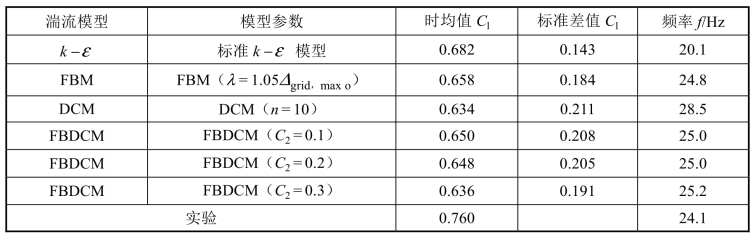
表4-6综合给出了分别采用标准k-ε模型、FBM、DCM和FBDCM得到的时均升力系数、升力系数的标准差以及升力的特征频率。值得注意的是，DCM预测的升力特征频率偏大，FBM和FBDCM预测的结果基本一致。这是由于在云状空化中，反向射流的产生和发展会直接导致空泡团的断裂和脱落现象，而反向射流往往发生在含汽量较小近壁水汽混相区域，在这部分区域内，FBM将起到主导作用。

表4-6　不同湍流模型预测得到的水翼升力系数的时均值、标准差值和频率

上述湍流模型的主要区别在于对湍流黏度的计算方法不一样。图4-23给出了采用不同湍流模型计算得到的水翼周围流场的湍流黏度分布图。蓝色区域代表湍流黏度较小的区域，红色区域代表湍流黏度较大的区域。标准k-ε模型在未修正前，过高地预测了湍流黏度，并且，湍流黏度分布随时间变化不是很明显，抑制了空化流场的非定常特性。FBDCM顾及了FBM和DCM的不同作用区域：对附着在翼型前缘的空穴区域进行密度修正，对空穴尾端的水汽混合区进行滤波修正，同时降低了空穴内部和水翼尾部的湍流黏度。在FBDCM中，可以通过改变C2的大小以调节FBM和DCM在流场中的比重。如图4-23所示，当C2=0.1时，FBM在混合模型中将起到主要作用；当C2=0.3时，DCM在混合模型中将起到主要作用，所预测的湍流黏度分布与DCM较为一致。

图4-23　不同湍流模型预测得到的水翼周围的湍流黏度云图随时间的变化过程（σ=0.80，α=8°，Re=7×105）（见彩插）

图4-24给出了分别应用3种模型计算所得空穴形态及其与实验观测结果的对比。不同湍流模型预测得到的水翼周围湍流黏度分布的差异势必会导致云状空穴发展过程的不同。标准k-ε模型过度预测了水翼周围的湍流黏度，抑制了空穴的发展和空泡脱落等非定常流动细节，预测得到的附着型空穴的最大长度明显小于实验观察，而FBM、DCM和FBDCM所得的计算结果都清楚地描述了附着型空穴发展-断裂-空泡脱落变化过程。相对而言，采用DCM得到的空化区域（尤其是最大空穴长度）相对较大。

图4-24　不同湍流模型预测得到的空穴形态云图随时间的变化过程（σ=0.80，α=8°，Re=7×105）（见彩插）

图4-25给出了附着型空穴长度随时间的变化。实验结果表明，附着型空穴长度的发展过程可以分为两个阶段：第一个阶段是空穴持续生长的过程（0～0.375Cycle，Cycle为一个完整的云状空化的发展周期），在该阶段，透明状空穴几乎呈线性增长直至最大长度；第二个阶段是反向射流向水翼前缘的发展过程，在第二个过程的起始阶段（0.375～0.80Cycle），附着在水翼上的空穴长度只是小范围地波动。随后，当反向射流达到水翼的前缘时，如图4-26（c）所示，空穴突然断裂，因此附着在翼型上的空穴长度会骤减。

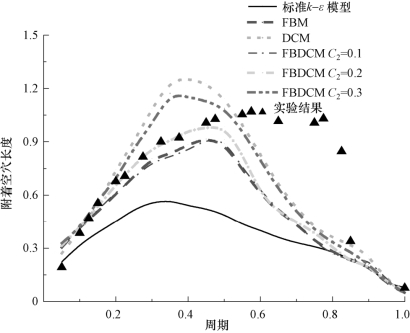
图4-25　不同湍流模型预测得到的附着型空穴长度随时间的变化过程（σ=0.80，α=8°，Re=7×105）

图4-26　反向射流及空穴断裂示意图（σ=0.80，α=8°，Re=7×105）

（a）30% Cycle；（b）67.5% Cycle；（c）90% Cycle

通过对比采用不同湍流模型计算得到的结果（数值计算结果中，确定含汽量αv=0.1为空穴边界），可以发现标准k-ε模型预测的结果与实验结果存在较大的差异。经过湍流黏度修正后，在空穴长度发展的第一个阶段内，FBM、DCM和FBDCM均较为合理地预测了附着型空穴长度的非定常变化。略有不同的是，与实验结果对比，采用FBM得到的空穴长度偏小，而采用DCM得到的空穴长度则偏大。相对而言，采用FBDCM（C2=0.2）得到的附着型空穴长度的发展过程与实验结果最为接近。值得注意的是，上述几种模型在模拟空穴发展的第二个阶段时都产生了比较大的偏差，均过早地预测了空穴的断裂和空泡的大尺度脱落过程。在空化现象的数值计算中，空化模型通过调节汽液相间的传输过程，用于捕捉空穴的生成、空穴断裂和空泡脱落、溃灭等动态行为。因此，空化模型的选择对预测空穴的非定常发展过程及内部流场结构有着更为重要的影响。在后续内容中，将重点对相关空化模型进行评价与应用，以期进一步改善数值计算模型的预测精度。

为了进一步说明不同湍流模型对空化流场结构的影响，图4-27给出了在数值计算得到的云状空化条件（σ=0.80）下，特征剖面上沿主流方向上的时均速度分布，并与实验结果进行了对比。剖面x/c分别位于20%、40%、60%、80%、100%、120%位置处。

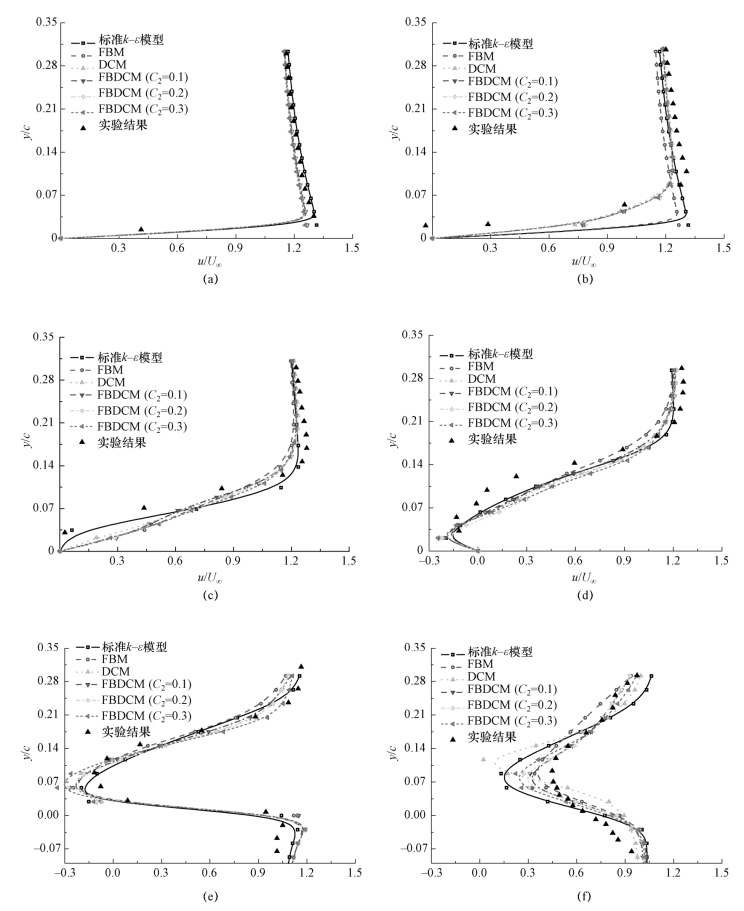
图4-27　应用不同湍流模型得到的特征剖面处，沿主流方向上的时均速度分布与实验结果的对比（σ=0.8°，σ=8°，Re=7×105）

从实验结果可以看出，在x/c=0.2与x/c=0.4位置处，空穴外部平均速度的大小均接近于主流平均速度，而在空穴内部，速度值迅速减小，呈现出很强的剪切层结构。从图4-27中可以看出，采用不同湍流模型得到剖面上时均速度变化趋势基本一致。在空穴内部，时均速度都经历了逐渐增大的一段过程，并逐渐与主流速度达到一致；在空穴外部，上述湍流模型均较好地描述了时均速度分布。在x/c=0.6与x/c=0.8位置处，由于此处的空穴厚度较大，速度剪切层区域也更为显著，数值计算与实验得到的时均速度分布在一定程度上显示了近壁区域的反向射流现象。在x/c=1.0与x/c=1.2的翼型尾部流场中，实验结果表明，时均速度呈大幅度的变化趋势，翼型尾端汽-液两相区的大规模非定常运动加强了空穴区域的动量交换，产生了空泡团的旋涡分离现象，对该区域内的时均速度分布产生了较大的影响。由图4-27（f）可以看出，与其他湍流模型相比，采用FBM和FBDCM计算得到的翼型尾部流场的时均速度分布与实验值较为吻合。这是由于上述两种模型对水翼尾缘的湍流运动采用了直接求解的方法，精确计算了大尺度涡团的流动，使得时均速度分布具有更好的空间分辨率。

湍流模型对于非定常空化流动的数值预测有着非常显著的影响。本节分别介绍了面向工程应用的空化湍流模型，包括考虑空间尺度效应的滤波器模型和考虑气液多相特征的密度修正模型。从相关分析可以看出，对于上述两种方法：前者希望通过解决对于黏度系数的过预测，提高对于非定常流动计算过程的预测精度，是针对整个流动计算区域的，包括了空化和非空化区域；后者注重空化多相流特征，仅针对空化区域。两种方法均可有效降低流场计算的湍流黏度，从而提高对非定常空化流动的预测精度。通过对非定常空化流动不同特征区域的物理机制的认识，由此构建了一种基于混合密度分域的湍流模型，在数值建模中充分考虑了空化多相流动和湍流多尺度效应等流动特性的表达。