由于空化区内含有大量的水蒸汽，是一种水-汽混合介质。考虑到汽-液两相混合密度的变化对湍流黏度的影响，可应用一个密度函数代替式（4.17）中的混合密度ρm，形成了一种基于密度的修正方式（Density Corrected Model，DCM），湍流黏度采用下式进行计算：

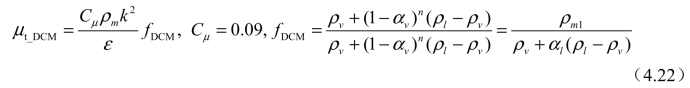
图4-14给出了式（4.22）中混相指数n取不同值时，经修正后的混相密度与汽体体积分数的关系曲线（横坐标为汽体含量αv，纵坐标为经修正后的混相密度ρm1）。从图中可以发现，当水蒸汽含量相同时，引入密度修正函数后，在水蒸汽含量较小的汽-液混合区域，可以减小空化区域内的湍流黏度，从而减少湍流应力对空化流计算的影响，以期合理预测反向射流、空泡脱落等非定常流动行为。

图4-14　经修正后的混相密度与汽体体积分数的关系曲线

基于密度修正的方法由于考虑了空化汽-液多相流场的特点，从而成为发展空化流动计算的潜在方向，事实上该方法已得到了广泛的应用。但是，对于混相指数n的取值，不同文献并不统一，均没有给出相关的解释和说明。n值的大小直接体现了计算中汽-液混相区域的当地可压缩性，势必会对数值计算结果产生重要的影响。图4-15给出了分别采用n=2、n=10和n=20计算得到的经修正后的时均混相密度函数的分布，随着混相指数n值的增大，低密度区域逐渐增大。图4-16进一步给出了不同混相指数n值下，绕水翼的湍流黏度分布，低湍流黏度区域对应于低密度的空化区域。值得注意的是，与FBM的修正方式不同，DCM主要对近壁空化区域内的湍流黏度进行了修正，该部分的湍流黏度远小于流场中的其他区域，而混相指数n的取值大小对远离水翼壁面的黏度分布影响不大。随着混相指数n值的增大，低湍流黏度区域逐渐扩大，并且空化核心区域的湍流黏度也逐渐减小。

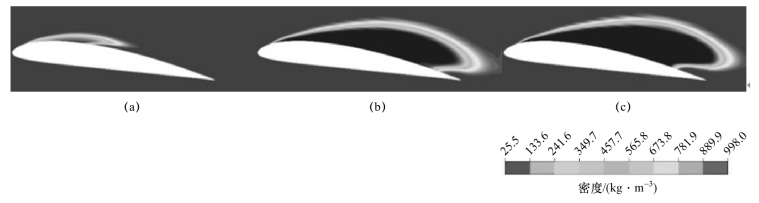
图4-15　不同混相指数n值预测得到的混相密度函数：ρm1=ρv+（1-αl）n（ρl-ρv）的分布（σ=0.80，α=8°，Re=7×105）（见彩插）(www.daowen.com)

（a）n=2；（b）n=10；（c）n=20

图4-16　不同混相指数n值预测得到的时均湍流黏度分布（σ=0.80，α=8°，Re=7×105）（见彩插）

（a）n=2；（b）n=10；（c）n=20

图4-17描述了混相指数分别为2、10和20时，绕水翼非定常空化发展过程及周期的差异。从图中可以看出，在不同n值下，数值计算得到的非定常空穴的发展过程均呈明显的周期性变化。当混相指数n=2时，附着在水翼上的最大空穴长度要明显小于n=10时模拟得到的结果。当混相指数n=10时，计算得到的斯特劳哈数Stc=0.195，比实验值略大。值得注意的是，当混相指数n值增大到一定程度后，如混相指数n=10和n=20，预测的结果基本相同，这是由于当混相指数n=10和n=20时，如图4-17所示，混相密度函数与汽相体积分数的关系曲线区别不大。

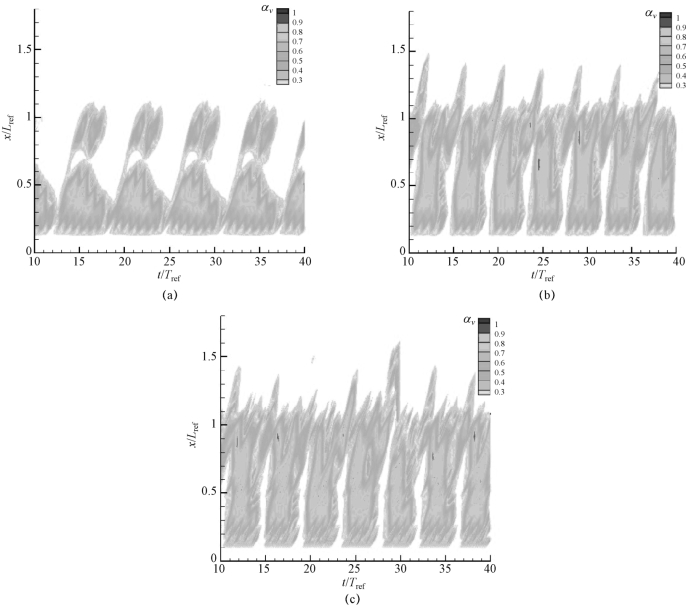
图4-17　不同混相指数n值预测得到的云状空化水汽含量随时间变化的云图（σ=0.80，α=8°，Re=7×105）

（a）n=2；（b）n=10；（c）n=20