标准k-ε模型是典型的RANS湍流模型。它把涡流黏度和湍流动能及湍流动能耗散联系在一起，该模型由Launder和Spalding于1972年提出，对于均相平衡流动的数值计算，标准k-ε模型的控制方程如下：

标准k-ε模型主要问题在于，它是基于定常平均流动，黏度由湍流动能和耗散率求解，这暗示着模型反馈的流场主要湍流尺度很大。为了解决标准RANS模型在处理多重湍流尺度决定的动力流动结构的缺陷问题，Johansen等提出了滤波器湍流模型（Filter Based Model，FBM）。FBM实际上是由LES和RANS模型结合起来建立的混合模型，通过在流域中加入滤波器，湍流尺度小于滤波尺度的流动结构将会采用k-ε湍流模型求解。当滤波尺度小于RANS模型反馈的湍流特征尺度时，就采用FBM进行计算，这样可以允许流动结构的发展不会因为模型的有效黏性发散。在均质多相流模型中，k方程和ε方程仍采用式（4.16）的形式，而湍流黏度修正为

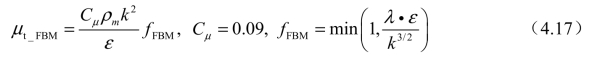
式中，fFBM为滤波函数，由滤波尺度λ和湍流特征尺度的比值大小决定。在标准k-ε湍流模型中加入滤波函数后，对于湍流特征尺度小于滤波器尺度的湍流（λ＞＞k3/2/ε），采用标准k-ε模型进行模拟。

当湍流尺度较大时（λ＜＜k3/2/ε），如远离壁面的流动区域，其湍流黏度为

从而有效地降低了计算流场中的湍流黏度，以期提高对于非定常流动计算过程的预测精度。为了验证FBM在空化流动计算中的适用性，下面分别对回转体和水翼的空化绕流算例进行了计算和分析。

首先，分别应用FBM和标准k-ε模型计算了回转体绕流问题，并与经典实验结果进行了对比。在计算中，计算区域和边界条件的设置完全与实验保持一致，回转体近壁区域采用O形结构化网格划分，这样可以较好地匹配回转体头部的形状。为了更准确地计算空化流动，如图4-3所示，在回转体周围近壁区域进行了网格加密，整个流域的网格总数约为1×105，近壁的边界层区域分布约有100个节点。在计算中，以回转体直径为特征长度的雷诺数为ReD=1.36×105。湍流模型分别采用标准k-ε模型和FBM。在FBM中，选取的滤波尺度为10为回转体周围O形格的最大尺度。滤波尺度的选取直接影响到流场中湍流黏度大小，进而会对空化流场的计算结果起着重要的作用，这方面的研究将在后续内容中进行详细的介绍。

图4-3　回转体周围的网格分布

图4-4（a）为σ=3.0时（此时，空化数较大，无明显的空化现象发生，可视为单相流动），应用FBM和标准k-ε模型预测得到的回转体表面的压力分布与Rouse和McNown的实验结果的对比情况，图中的横坐标为模型表面位置的无量纲化参量（其中S表示从前驻点开始沿轴对称体表面到取值点的弧长，d表示轴对称体横截面的直径），纵坐标为压力系数计算和实验均表明，轴对称体表面的压力系数呈现出以下的分布规律：沿流动方向由驻点最大值急剧下降；当到达旋涡分离区时，压力系数下降到最小并逐渐趋于稳定；接着压力系数逐渐上升，而后达到一个稳定区域。对于标准k-ε模型，FBM预测得到的回转体表面的压力曲线与实验测量值吻合得更好。图4-4（b）进一步比较了上述两个湍流模型预测得到的分离点及再附着点位置与Katz的实验结果的对比，Katz通过实验观测，分析了绕回转体肩部的旋涡分离区。从图中可以看出，湍流模型的选择对预测再附着位置区域有着显著的影响，标准k-ε模型所预测的分离再附着点的位置与实验结果有明显的差异，FBM预测得到的再附着位置明显延迟，与实验结果比较一致。

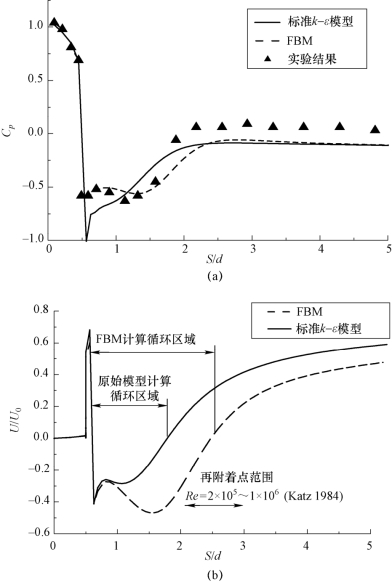
图4-4　应用FBM和标准k-ε模型预测得到的绕回转体的单相流动特性对比

（a）回转体表面的压力分布；（b）回转体表面的速度分布

图4-5进一步对比了σ=0.5时，应用FBM和标准k-ε模型获得的预测结果。从图中可以看出，FBM预测得到的低压空化区域明显要大于标准k-ε模型的预测结果，并且FBM预测得到的时均空穴长度与实验测量值有较好的吻合。

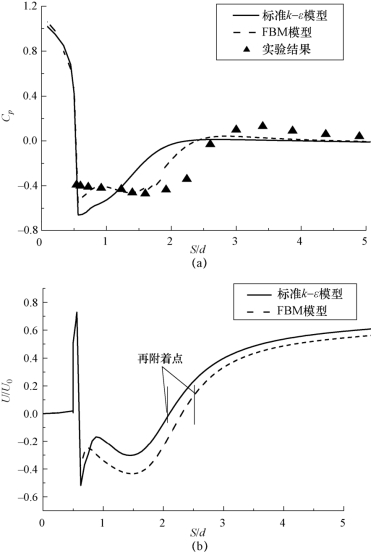
图4-5　应用FBM和标准k-ε模型预测得到的绕回转体的空化流动特性对比

（a）回转体表面的压力分布；（b）回转体表面的速度分布

为了进一步评价FBM对非定常空化流动的应用，基于第2章的绕Clark-Y型水翼的空化流动实验结果对FBM的计算结果进行了评价与分析。在计算中，几何模型、计算区域的尺寸及工况条件设置与实验保持一致（图4-6）。图4-6为边界条件设置及网格划分示意图。翼型前端的区域采用O形结构化网格划分，可以较好地匹配翼型头部的形状。计算区域的入口距翼型前缘约为4c，出口距翼型尾缘的距离为5c。如图4-6（b）所示，在翼型周围近壁区域及尾缘区域进行了网格加密。计算采用了速度入口，平均静压出口，上、下边界设为固壁。在相关文献中，针对该算例已对网格以及时间步长的无关性进行了分析，在此不再赘述，非定常计算的时间步长设定为Δt=7×10-4。

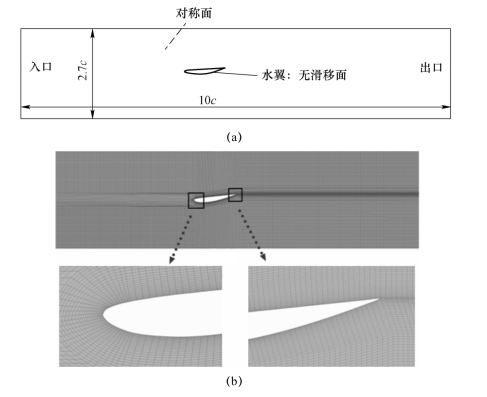
图4-6　计算区域及边界条件设置和Clark-Y型水翼周围的网格划分示意图

（a）绕Clark-Y型水翼的计算区域及边界条件设置示意图；（b）水翼周围的网格划分示意图

计算中，在流场入口的边界上，需要定义流场的湍流参数。这里，通过湍流强度I和湍流黏度比值μt/μl|inlet进行进口边界上湍流条件的设置。计算中，进口边界上的湍流参数如下：

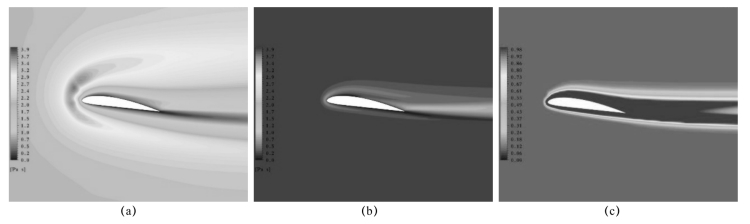
根据实验给出的数据，如图4-7所示，速度进口处的湍流强度I设定为0.02，但湍流耗散率无法得到准确值。为了解湍流模型对进口μt/μl|inlet黏度比的敏感程度，图4-7～图4-9分别给出了进口μt/μl|inlet黏度比分别为1 000、2 000和5 000时，针对绕水翼的片状空化流动（σ=1.40）进行定常计算得到的湍流黏度μt及滤波函数min（1，Δ/（k1.5/ε）的分布情况（在FBM模型中，滤波尺度的取值为10Δgrid，maxo，Δgrid，maxo为水翼周围O形格的最大尺度）。采用标准k-ε模型的计算结果表明，随着进口湍流黏度比的增大，水翼周围的湍流黏度也增大，即计算结果对进口μt/μl|inlet黏度比有较强的依赖性。FBM中滤波函数的应用有效地调节了流场中的湍流黏度。从计算结果来看，当μt/μl|inlet黏度比增大时，滤波函数的绝对值降低，从而使流场中的湍流黏度整体分布变化不大。与标准k-ε模型相比，FBM对进口μt/μl|inlet黏度比的敏感程度大幅降低，有助于提高计算的鲁棒性。

图4-7　进口μt/μl|inlet为1 000时，计算得到的湍流黏度分布（σ=1.40，α=8°，Re=7×105）

（a）标准k-ε黏度μt；（b）FBM黏度μt；（c）min（1，Δ/（k1.5/ε）

(www.daowen.com)

图4-8　进口μt/μl|inlet为2 000时，计算得到的湍流黏度分布（σ=1.40，α=8°，Re=7×105）

（a）标准k-ε黏度μt；（b）FBM黏度μt；（c）min（1，Δ/（k1.5/ε）

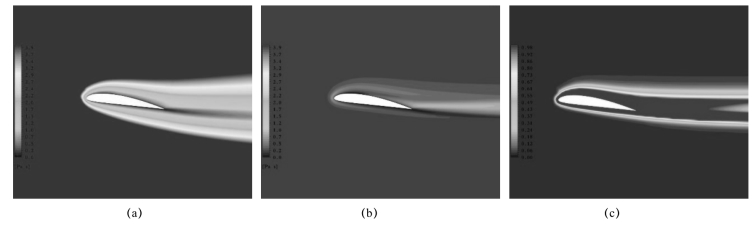
图4-9　进口μt/μl|inlet为5 000时，计算得到的湍流黏度分布（σ=1.40，α=8°，Re=7×105）

（a）标准k-ε黏度μt；（b）FBM黏度μt；（c）min（1，Δ/（k1.5/ε）

图4-10给出了应用标准k-ε模型及FBM得到的速度分布云图。在相同的计算条件下，FBM可以模拟出大尺度脉动现象，捕捉到非常明显的非定常涡团结构。而标准k-ε模型则将流场中不同尺度的涡同等对待，通过平均运算将脉动运动的时空变化细节抹平，对大尺度分离流动的预报性较差，所能捕捉到的涡团结构远不如FBM丰富。

图4-10　标准k-ε模型及FBM预测得到的速度分布云图（σ=1.40，α=8°，Re=7×105）

（a）标准k-ε模型；（b）FBM

在上述FBM的计算应用中，尽管对滤波函数中滤波尺度的取值没有经过严格的试算工作。从总体而言，相较标准k-ε模型，FBM对提高计算的鲁棒性和预测流场中的非定常特征有较好的改进。为了更好地对非定常特性非常显著的云状空化流动进行模拟，应在前面研究基础上，选取一个合适的滤波器尺度。这里，针对绕水翼的云状空化流动（σ=0.80），对不同滤波尺度条件下的计算结果进行了分析，讨论了FBM中滤波尺度对空化绕流流场的影响。在计算中，对选取的滤波尺度在一定范围内进行了严格的试算，根据云状空化流动特点及前期计算中的取值经验，计算中选取的滤波尺度从大到小依次为：10Δgrid，maxo、3.23Δgrid，maxo、1.61Δgrid，maxo和1.05Δgrid，maxo，其中，Δgrid，maxo为水翼周围O形格的最大尺度。图4-11给出了在不同滤波尺度下，水翼周围的时均湍流黏度分布。滤波尺度的大小直接影响远流场及水翼尾缘处的湍流黏度分布：当滤波尺度较大时（λ=10Δgrid，maxo和λ=3.23Δgrid，maxo），由于在云状空化流动中，空穴尾部流场存在大尺度的旋涡，速度梯度较大，此区域的湍流动量生成项Pk较大，因此会过高估计空穴后部湍流能量k，从而导致湍流黏度μt偏大。由时均空穴形态可以看出，较高湍流黏度阻碍了空穴的发展，仅在水翼前缘形成了附着型空穴。如图4-11（c）和（d）所示，随着滤波尺度的减小，流场中的湍流黏度也逐渐减小。图4-12描述了在不同滤波尺度下，时均空穴形态及流场分布。从图可以看出，在较小的滤波尺度下（λ=1.61Δgrid，maxo和λ=1.05Δgrid，maxo），预测得到的空穴形态有明显的增大，时均空穴形态与实验比较接近。此时，空穴形态分为两个明显的特征区域：一是附着在水翼前缘的附着型空穴；二是在水翼尾缘，由反向射流所形成的空泡旋涡脱落区域。当λ=1.05Δgrid，maxo时，所预测得到的时均空穴形态与实验结果最为接近。

图4-11　不同滤波尺度取值预测得到的时均湍流黏度分布云图（σ=0.80，α=8°，Re=7×105）（见彩插）

（a）λ=10Δgrid，maxo；（b）λ=3.23Δgrid，maxo；（c）λ=1.61Δgrid，maxo；（d）λ=1.05Δgrid，maxo

图4-12　不同滤波尺度取值预测得到的时均空穴形态及流场与实验结果的对比（σ=0.80，α=8°，Re=7×105）（见彩插）

（a）实验；（b）λ=10Δgrid，maxo；（c）λ=3.23Δgrid，maxo；（d）λ=1.61Δgrid，maxo；（e）λ=1.05Δgrid，maxo

滤波尺度的大小将会对云状空化非定常流动结构及其准周期演化过程的预测有重要的影响。如图4-12所示，取水翼吸力面附近的曲线A作为监测线。图4-13给出了水汽含量在时空上的变化过程，该方法形象地描述了附着型空穴的发展和空泡脱落过程。图中纵坐标表示沿弦长方向的长度，横坐标为时间，云图为水蒸汽含量，深色区域对应的含汽量较大。同时，图4-13还给出了水蒸汽含量云图及相应时刻的水翼相对位置图。

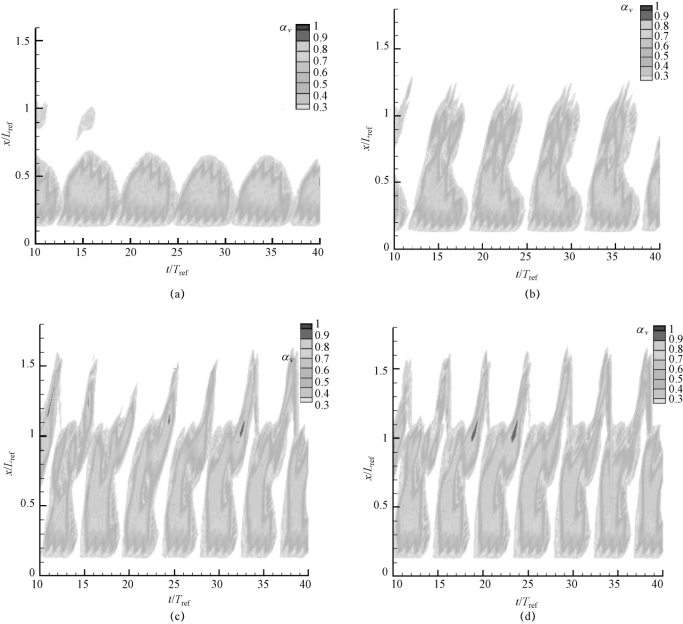
图4-13　不同滤波尺度取值预测得到的云状空化水汽含量随时间变化云图（σ=0.80，α=8°，Re=7×105）

（a）10Δgrid，maxo；（b）3.23Δgrid，maxo；（c）1.61Δgrid，maxo；（d）1.05Δgrid，maxo

图4-13描述了在不同滤波尺度下，绕水翼非定常空化发展过程及周期的差异。图中，Tref和Lref分别定义为

式中，c为水翼的弦长；U∞为主流方向速度。

与U∞对应的斯特劳哈数Stc定义为

从图4-13可以看出，在不同滤波尺度下，数值计算模拟得到的非定常空穴的发展过程均呈明显的周期性变化，其差异主要是空穴的发展周期上。

（1）当滤波尺度较大时，如λ=10Δgrid，maxo和λ=3.23Δgrid，maxo，所预测得到的附着型空穴长度和核心空化区域较小，并且无法捕捉到水翼尾部的脱落空泡云。空穴形态非定常变化的平均周期分别为6.2Tref，其对应的斯特劳哈数Stc=0.16，这与实验测量结果的斯特劳哈数0.175有一定的差异。

（2）当滤波尺度为λ=1.61Δgrid，maxo和λ=1.05Δgrid，maxo时，在附着型空穴的发展过程中，最大空穴长度可达到1.1c左右，并能准确地捕捉到空泡云的脱落现象。在上述两个较小的滤波尺度下，计算得到的斯特劳哈数Stc=0.18，与实验测量结果比较接近。

RANS模型基于雷诺时均构建，在处理由多重湍流尺度决定的非定常流动结构存在一定的困难，其主要原因是因为湍流黏度的过预测。LES方法也是最有可能提高空化湍流流动工程计算精度，从而推动计算空化流体动力学向精确定量预测技术转变的方法。从客观上讲，LES相对RANS模型而言，计算成本较大。FBM实际上是RANS和LES模型相结合建立的混合模型，希望通过解决对于黏度的过预测，提高对于非定常流动计算过程的预测精度，是针对整个流动计算区域的，包括了空化和非空化区域。与FBM类似，近年来，分离涡模型（Detached Eddy Simulation，DES）、局部时均化模型（Partially-Averaged Navier-Stokes Model，PANS）等混合模型在空化流动计算中也得到了应用。上述模型的基本核心均为通过模型参数或者滤波尺度实现由RANS模型向LES或DNS的平滑过渡。