对于空化现象，理论研究最早建立在Helmoholtz和Kirchhoff提出的自由流线理论（free-stream-line theory）和速度图法（Hodograph method）基础上。在该理论中，研究空化问题，需要给出空穴的闭合模型，其主要包括以下几种：映像模型、尾流模型和回射流模型。其共同的假设为空泡内部的压力为常数，空泡面为自由流线，但是均未涉及空泡内部的流动。以上的各类空泡流数学模型，从理论上有效地解决了一些二维定常空化流问题。面对大多数复杂的空化流动问题，解析方法面临着较大的困难。研究者将研究重点逐步转移到数值模型中来，基于对空化流动现象，主要发展出以下两种数值计算方法。

第一种方法认为空穴内是连续的气（汽）体，汽相和液相之间存在清晰的界面，界面上给出运动学和动力学边界条件，界面位置采用迭代的方法获得。基于上述认识，应用最多并且发展最为完善的是边界元计算方法（Boundary Element Method，BEM）。边界元计算方法通常应用于定常附着型空化和超空化的流动计算，可以较好地预测空化流动的整体行为。但是，该模型必须应用尾流模型近似空穴尾部闭合区的两相流行为，在假设过程中，很难引入明确的物理意义。因此，此种方法很难处理由于闭合区的流场特性决定的空化非定常流动行为。

第二种方法，基于N-S方程的空化流动计算方法得到了普遍的重视。在基于N-S方程的计算框架内，研究者普遍采用双流体模型和均质平衡流模型（Homogeneous Equilibrium Flow Model，HEFM）。双流体模型将汽-液两相都看成是充满整个流场的连续介质，针对两相分别建立质量、动量方程，并通过相界面间的相互作用将两组方程耦合起来。均质流模型将汽-液两相混合物看作一种均匀介质，相间没有相对速度，流动参数取两相相应参数的加权平均。考虑到该方法运用的成熟度和易用性，主要在均相流的框架内讨论有关流动模型的建立。图4-2所示为均相流模型示意图。

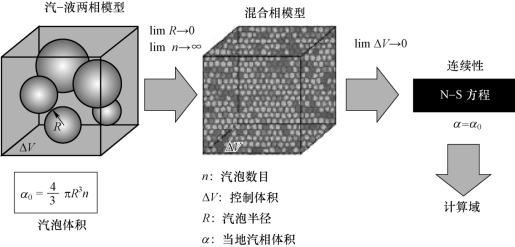
图4-2　均相流模型示意图(www.daowen.com)

假设汽-液两相为均相流动，相间无速度滑移，考虑汽-液相间的传输速率，汽-液两相的连续方程和动量方程如下：

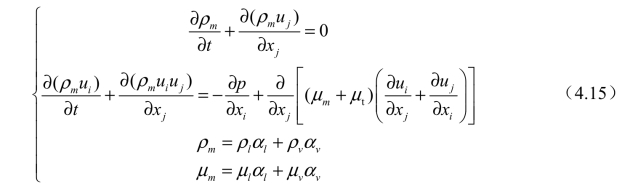
式中，下标“i”和“j”分别代表坐标方向；u和p分别为速度和压力；　μt为湍流黏度；ρm为混合密度；μm为混合相的动力黏度，按汽-液两相体积分数加权平均后得到。

由于增加了未知量，在空化流场的模拟之中，除了湍流封闭以外，还要求解密度场进行空化模拟，必须寻求建立混合介质密度与其他物理量之间的关系，或耦合入空化模型。基于不同密度场ρm的确定方法，空化模型根据不同的理论和假设，主要分为正压流体状态方程模型（Barotropic Equation Model，BEM）和质量传输方程模型（Transport Equation Model，TEM）两类。