基于激光多普勒测振系统，应用上述瞬态信号分析与振动评价方法，获得了给定工况下，水翼结构振动速度随时间的演变以及相应的频域和时频图，如图3-42所示。其中，来流速度U=8 m/s，水翼攻角分别为4°、6°和8°。当来流攻角为4°时，结构振动速度呈正弦分布，主频值838 Hz清晰可辨。当来流攻角增大时，非共振工况下的主频值分别为154 Hz（6°）和149 Hz（8°），同时结构振动速度显著减小。

为了进一步研究绕水翼单相流激共振特性，图3-43给出了不同攻角下，绕水翼单相流动的结构振动速度频谱图。流激振动的主频值随着来流攻角的变化而变化，当其与水翼的固有频率相吻合时，结构将发生共振，振动幅度明显增加，同时伴有明显的噪声。由图3-43可知，当来流攻角小于4°时，流激振动频率与结构一阶扭转频率吻合，为840 Hz。此时结构发生明显的扭转变形，振动幅度显著增加；当来流攻角大于4°时，共振现象消失。

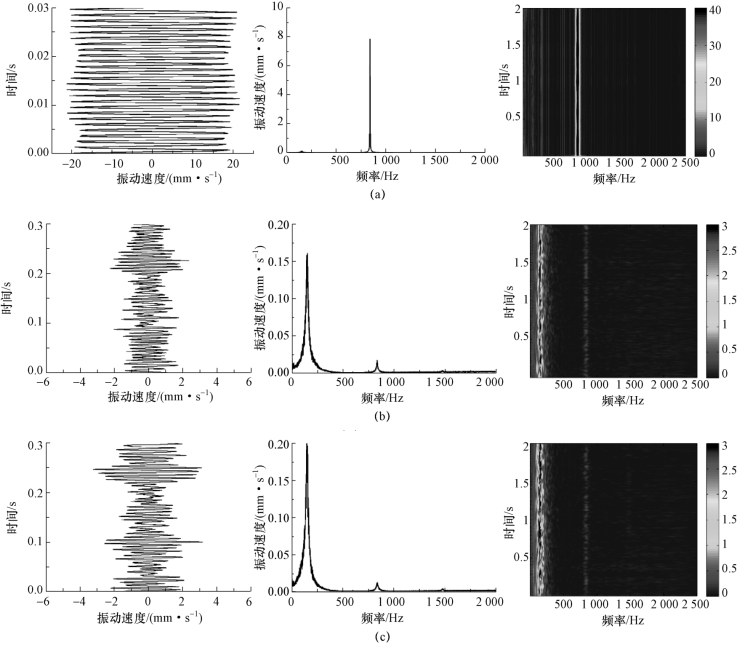
图3-42　绕不同攻角水翼单相流动结构振动速度的时域、频域和频谱图（U=8 m/s，Re=8.0×105）（见彩插）

（a）α=4°；（b）α=6°；（c）α=8°

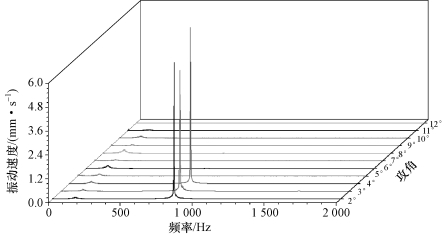
图3-43　绕不同攻角水翼单相流动结构振动速度频谱图（U=8 m/s，Re=8.0×105）

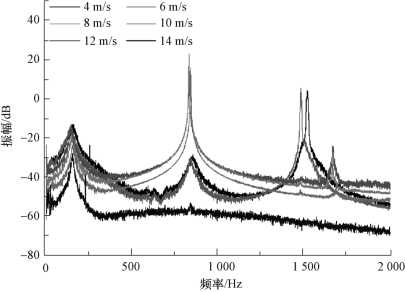
当系统发生共振时，流场速度对共振频率有着显著影响，且在特定工况下发生“自锁”，即流动激发振动幅度足够大，以至于结构的振动频率锁定在特定值而不随流速的变化而变化。图3-44给出了来流攻角α=4°时，不同来流速度下的水翼结构振动速度频谱图。由图可知，基于振动速度的傅里叶变换明显捕捉到的前三阶振动频率分别为f1=150 Hz、f2=840 Hz和f3=1 670 Hz，该频率随来流速度的增加基本保持不变，而当来流速度增大至12 m/s时，绕水翼流动发生失速，此时流场激发的振动频率f=1 480 Hz。

(www.daowen.com)

图3-44　不同来流速度下的水翼结构振动频谱图（α=4°，单相流动）

对NACA0009水翼结构的涡激振动现象进行观测，图3-45给出了来流速度U=13 m/s，空化数σ=0.5时，绕金属材料水翼瞬态流动的流场结构演变与涡激振动形态。在实验中，水翼尾缘形成稳定的卡门涡街，水翼结构发生明显扭转变形，同时伴随有强烈的噪声。如图3-45（a）所示，当t=T0时，水翼尾缘一侧旋涡结构脱落，另一侧旋涡结构开始形成。从t=T0发展至t=T0+36% Tcycle时，如图3-45（a）和（b）所示，旋涡结构不断增长，并逆时针旋转向下游运动。从t=T0+67% Tcycle发展至t=T0+89% Tcycle时，如图3-45（c）和（d）所示，旋涡结构脱落，另一侧旋涡结构开始形成，并与一侧旋涡结构交错对称分布。两侧旋涡结构的稳定、周期性形成、发展，形成交替脱落的卡门涡街。结合Ausoni、Zoberi等对该水翼进行的结构振动速度测试结果发现，尾缘涡结构周期性脱落引起的结构振动频率随来流速度的增加而增加。在该工况下，涡激振动频率为888 Hz，与实验观测到的旋涡脱落频率一致。

图3-45　绕金属材料水翼瞬态流动的流场旋涡结构与涡激振动形态（U=13 m/s，σ=0.5）

（a）t=T0；（b）t=T0+36%Tcycle

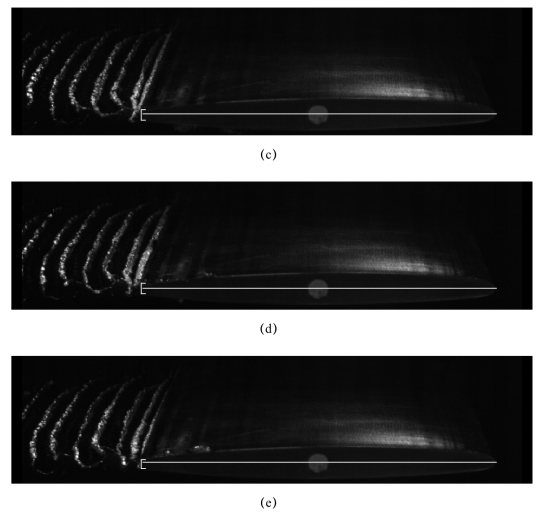
图3-45　绕金属材料水翼瞬态流动的流场旋涡结构与涡激振动形态（U=13 m/s，σ=0.5）（续）

（c）t=T0+67%Tcycle；（d）t=T0+89%Tcycle；（e）t=T0+110%Tcycle