空化的非定常过程包含了附着型空穴的生长、脱落、溃灭等复杂的非定常流动现象。空穴演变诱导的压力脉动可能带来振动、噪声、空蚀等不良影响。

图3-21给出了3种空化数条件下的空穴形态，每种空化数条件下分别给出了12个时刻的空穴形态，来流方向如图中黑色箭头所示。图中白色数字1、2、3、4分别表征4个传感器沿扩张段的分布情况。随着空化数减小，空穴波动幅度明显增大，并且逐渐呈现出周期性变化过程。σ=0.81时，扩张段的空穴呈现出游离状态，空穴尺度和波动幅度都很小，其向下游发展到1号和2号传感器附近，3号和4号传感器附近不存在空穴。σ=0.76时，喉口附近比较稳定的空穴为附着型空穴，流场中呈现出游离状态的空穴称为脱落型空穴。在T2+3.3 ms到T2+13.2 ms之间，附着型空穴逐渐生长，脱落型空穴逐渐向下游移动；在T2+13.2 ms到T2+26.4 ms之间，附着型空穴逐渐生长至最大尺寸，同时随着脱落型空穴不断向下游高压区移动，空穴团逐渐溃灭；在T2+29.7 ms到T2+39.6 ms之间，附着型空穴逐渐断裂、脱落，并且产生一些小尺度的脱落型空穴团，这些脱落的空穴团逐渐聚合、溃灭，不断向下游移动。在σ=0.73时，空穴形态的发展过程和在σ=0.76时呈现出相同的规律。但是，空化程度进一步加剧。

图3-21　不同空化数条件下的空穴形态发展过程

（a）=0.81；（b）=0.76

图3-21　不同空化数条件下的空穴形态发展过程（续）

（c）σ=0.73

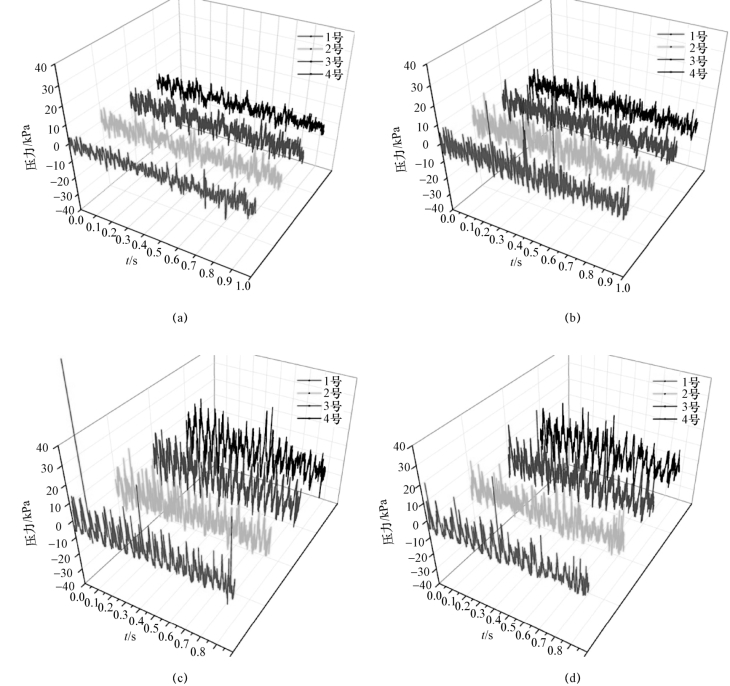
图3-22给出了上述工况下收缩扩张管段内不同监测点处压力随时间的变化。观察发现，当流场中没有空化产生时，单相水流作用下不同位置处压力均呈现出无规则的波动特征；当流场中产生尺度较小的空穴时，空穴发展到1号到2号传感器之间的区域，此时不同位置处压力的波动幅度明显增大，并且开始呈现出一些周期性波动特征；随着空化数的减小，当流场中空化现象进一步发展，呈现出大尺度周期性发展过程，此时不同位置处测得的压力波动幅度进一步增加，而且呈现出更加明显的周期特性。

(www.daowen.com)

图3-22　不同监测点处压力随时间的变化

（a）σ=1.8；（b）σ=0.81；（c）σ=0.76；（d）σ=0.73

下面进一步给出上述典型工况下无量纲空穴面积随时间的变化（图3-23），其中无量纲面积定义为S/Smax，S代表某一时刻的空穴面积，Smax代表1 s内的最大空穴面积。从图3-23可以看出，σ=0.81时的无量纲面积在0.9～1波动，波动幅度较小，而且波动规律不明显；σ=0.76和σ=0.73时，无量纲面积在0.5～1波动，波动幅度显著增加，而且呈现出周期性的波动特征。

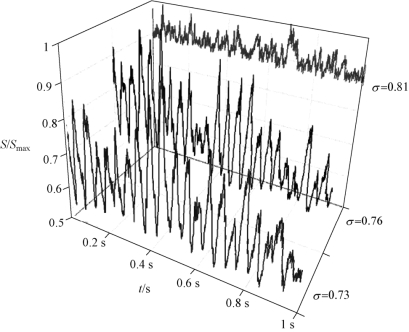
图3-23　无量纲空穴面积随时间的变化

图3-24给出了不同监测点处压力波动经过Choi-Williams变换得到的时频分布，图中曲线的颜色代表信号强度，从白色到黑色对应的信号强度逐渐增大。观察发现，当σ=1.8时，流场中没有产生空化，此时4个传感器测得压力变化的时频分布都没有连续、集中的频带。随着空化数的减小，当σ=0.81时，流道扩张段靠近喉口附近产生空穴，发展到1号和2号传感器之间，此时，4个传感器处压力变化的时频分布比较复杂，存在多条间断的、能量比 较集中的频带。这些频带分别对应着不同的频率，能量的分布特征与空穴面积的分布特征基本相同，说明该空化数条件下，空穴面积和相应的压力变化均呈现出无规则的非定常波动状态。当空化数减小至σ=0.76时，空化流动呈现出大尺度周期性发展过程，此时，4个传感器处压力变化的时频分布都呈现出比较一致的规律，4个传感器都存在一条能量集中的频带，对应的频率为20 Hz左右。同时，2号和3号传感器还存在更高频率的能量频带，如35 Hz处的能量频带。但是，其能量明显小于20 Hz频带对应的能量，因此说明4个传感器压力波动的主导频率为20 Hz，该频率和图2-23中空穴面积变化的主导频率相同。同时，在35 Hz处的次级主导频率与流场中的局部小尺度空穴波动有关，由于其引起的空穴面积变化很小，因此在空穴面积的频谱分析中没有表现出来。随着空化数的进一步减小，当σ=0.73时，压力的时频分布特征和σ=0.76时得到的特征相似，4个传感器都存在一条能量集中的频带，对应的频率为17 Hz左右。同时，2号和3号传感器还存在更高频率的能量频带，但是其能量明显小于17 Hz对应的能量大小。因此，说明4个传感器压力波动的主导频率为17 Hz，与图3-23中空穴面积变化的主导频率相同，其中2号和3号传感器出现的更高频率的能量分布将在下面进行讨论。

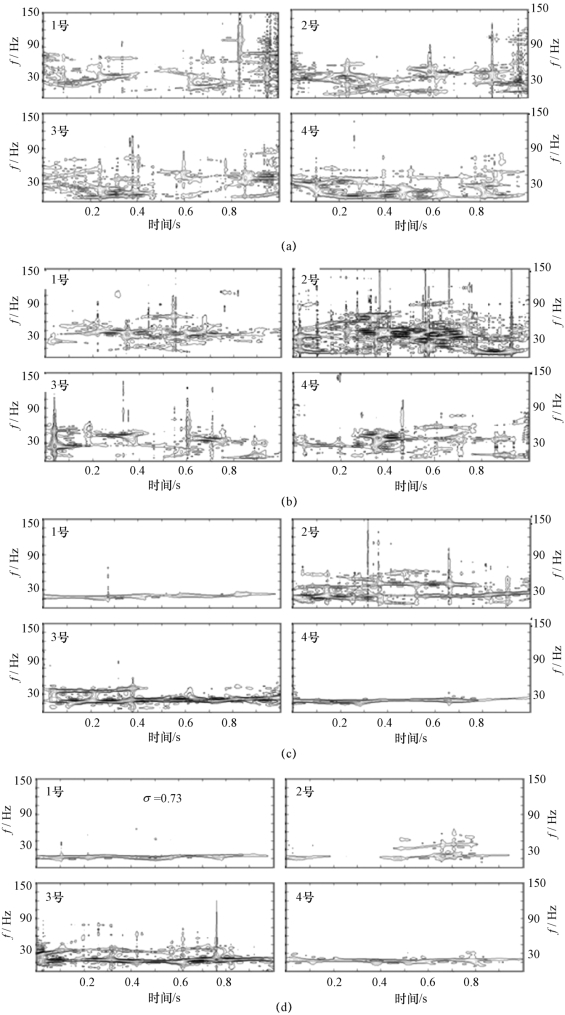
图3-24　不同监测点处压力波动的Choi-Williams变换

（a）σ=1.8；（b）σ=0.81；（c）σ=0.76；（d）σ=0.73

综上所述，在σ=0.76和σ=0.73时，不同传感器测得压力变化时频分布既有相似之处，也存在明显差异。观察图3-22中σ=0.76时对应的空穴形态发现，1号传感器主要受到附着型空穴生长、脱落过程的影响，因此压力波动信号的频率成分比较单一；4号传感器主要受到脱落型空穴团周期性聚合、生长、溃灭过程影响，使得信号频率成分也比较单一；2号和3号传感器既受到上述两种周期性发展过程的影响，同时还受到当地空穴脱落产生的小尺度空穴团的影响。由于这两种因素的共同作用，使得该处压力信号存在两种频率成分。另外，相对于大尺度周期性空穴生长和脱落变化而言，局部的脱落型小尺度空穴变化对2号和3号处压力波动的影响较小，因此该频率信号的能量较小。通过上述分析，说明各个传感器压力时频分布的特征与其所经历的非定常空穴形态变化有重要关联。