激光多普勒测振系统是一种基于光学多普勒效应的激光动态干涉仪，它是非定常空化流激振动特性有效的实验研究方法。基本原理如图3-6所示，通过发射一定频率的激光束，并对比经结构表面测点反射的激光束频率，利用多普勒效应计算结构表面测点的振动速度。

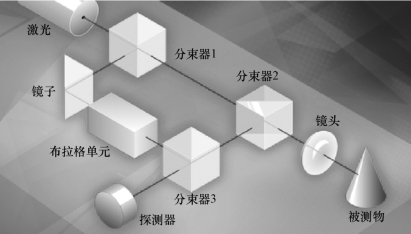
图3-6　激光多普勒测振仪基本原理

采用激光多普勒测振仪对结构的空化流激振动速度进行测量时，应该避免空泡对激光反射的干扰，以及减小壁面效应对结构振动的影响。同时，为了减少信号采集与数据分析的时空复杂度，总是希望采样频率尽量低，采样时间尽量短。但是，低的采样频率或短的采样时间常常会由于测试数据精度的降低而导致失败。根据采样定理，采样频率fs应大于被采集信号的2倍。同时，对所有的快速傅里叶变换（FFT）分析而言，用于计算的实际数据点数为2的n次幂（n为正整数），频率分辨率为fs/2 n。因此，在给定频率分辨率f0的前提下，采样频率fs的选取范围为

式中，m为最高有用频率的倍数，一般取2～4；fv为最高有用频率。

在给定采样频率下，采样时间T、采样点数N与频率分辨率f0的关系为

瞬态信号的预处理及综合评价方法对激振源的振动特征提取及特性描述都是至关重要的。传统的测试信号评价主要运用时域信息统计、频谱特征分析及时频状态描述等方法对测试信号进行处理与分析，综合诊断和评价测试信号反映的相关信息。

1.数据预处理

瞬态信号在实验采集过程中，难免会受到仪器精度、信号传输及环境噪声干扰等因素的影响产生无关信号及干扰信号。因此，在评价分析测试信号前需对其进行预处理，消除测试信号中的直流分量、不真实信号等，保证评价分析结果精确。

采集到的振动信号数据，由于测试仪器的基础运动、信号放大器随温度产生的零点漂移、传感器周围的环境干扰等，往往会偏离基线，偏离基线随时间变化的过程称为信号的趋势项。趋势项的存在将造成后续相关函数、功率谱函数分析结果的变形，尤其在积分后产生较大畸变。在研究中假设n阶多项式为

式中，pi为多项式系数。

根据最小二乘原理拟合趋势项多项式，求得多项式系数，从而实现去除趋势项。

预处理的另一个步骤是去噪。现有的信号消噪主要有两种方法：一是数字滤波器，通过设置通过频率限定值的方式获取有用信号信息，摒弃无关信号及干扰信号，主要有低通滤波器、带通滤波器和高通滤波器3种形式；二是基于信号滤波原理的小波去噪方法。两种方法都能较好地滤除干扰信号，成功地保留信号特征，但是数字滤波器有时会由于通过频率值的限定，滤除部分有用信号信息。因此，小波去噪方法更优于传统的数字滤波器。

运用小波分析进行信号的消噪处理是小波分析的一个重要应用。在实际的工程应用中，小波消噪的主要步骤包括信号分解、阈值量化及信号重构。首先对信号进行小波分解；然后以阈值等形式对小波系数进行处理，过滤干扰信号源；最后对信号进行重构，得到无噪无干扰的信号信息，开展下一步的分析处理。图3-7所示为基于小波信号消噪的过程示意图，图3-8所示为示例振动信号含噪信号和消噪后信号时域对比图。

图3-7　信号消噪过程示意图

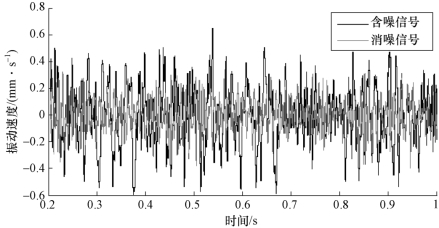
图3-8　示例振动信号含噪信号和消噪后信号时域对比图

2.时域分析

时域分析是根据系统的微分方程，以拉普拉斯变换作为数学工具，直接反映控制系统的时间响应。在实验中采集得到的信号一般都是随时间变化的数据序列，水翼振动测试中得到的信号可以看作稳态工况下周期性信号和随机信号的合成。从时域对比图3-8可以直观地反映测试量大小随时间的变化规律，时域波形分析直观、易于理解、包含的信息量大，对于某些明显特征信息，可以利用时域波形作初步和直观的判断。

实验直接采集到的信号是随时间变化的数据序列。研究采用模拟信号输出，输出信号与振动速度的换算关系为

(www.daowen.com)

式中，u为振动速度（mm/s）；k为模拟信号换算系数；ua为原始信号输出（mm/s）。

图3-9以水翼攻角α=6°，来流速度U=10 m/s，空化数σ=1.3流动工况为例，给出了此工况下结构振动速度信号的时域图，其中横坐标为时间，纵坐标为振动速度。图3-9直观地反映了振动速度随时间的变化规律。结合空穴形态的演变过程发现，水翼的振动速度也存在明显的周期性，随空泡的初生、发展、大尺度空泡团的形成、溃灭而逐渐增大，随着空泡团的脱落和前缘空泡的附着而减小。

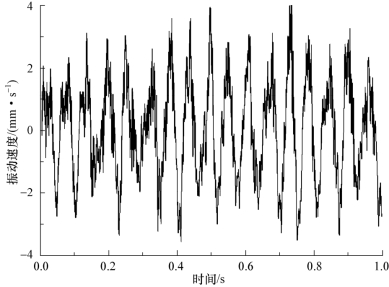
图3-9　水翼振动速度的时域图

图3-10所示为水翼振动位移的时域图，图3-11所示为水翼振动加速度的时域图。

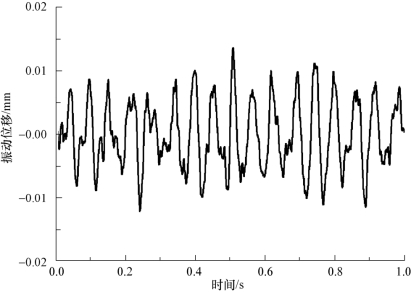
图3-10　水翼振动位移的时域图

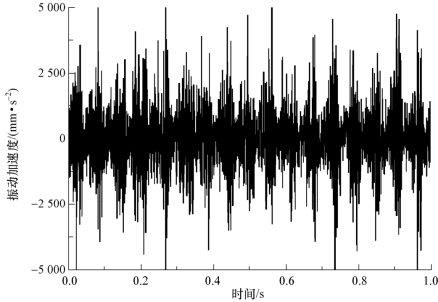
图3-11　水翼振动加速度的时域图

3.频域分析

目前，频谱分析是信号处理分析及故障诊断的最主要手段，是在频域中对采集信号分布情况的描述，能提供比时域波形更加直观的特征信息。对系统进行频域分析时，普遍采用快速傅里叶变换将信号从时域转变为频域。在频谱图3-12中，可清晰准确读取采集信号的频率特征，为准确获得激振源动态特性和振动规律提供可靠依据。

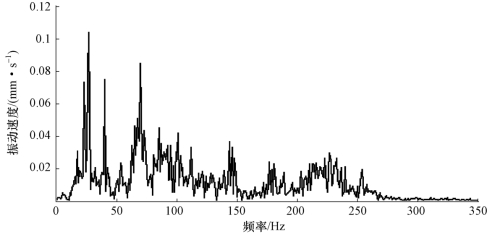
图3-12　示例水翼振动速度的频谱图

连续信号x（t）的傅里叶变换公式为

有限时长信号x（t）的傅里叶变换公式为

离散信号xn的傅里叶变换的计算公式为

截取时域信号进行傅里叶变换时，由于截断会造成部分信号泄漏，一般采用窗函数的办法来减小这种信号泄漏现象。常用的窗函数有矩形窗、指数窗、汉宁窗、汉明窗、Kaiser-base窗等。不同的窗函数有不同的效果，可以不同程度地提高主频处的幅值精度。

本书采用IEC规程推荐的汉宁窗，其计算公式为

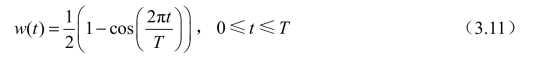
4.时频分析

时域分析直观地反映出测试信号脉动幅度随时间的动态变化信息，而频谱分析获得了测试信号脉动幅度在各个频率成分的变化信息，前者丢失了测试信号的频率成分信息，后者丢失了测试信号的时间信息。时频分析解决了这个问题，能实时反映测试信号频率成分随时间的变化信息，其目的在于构造一种时间和频率的密度函数，揭示信号中所包含的频率分量及其随时间的演化特性。目前，时频分析主要基于连续小波变换和短时傅里叶变换两种方式来实现。短时傅里叶变换的原理是在变换前乘上一个时间有限的窗函数，并假设非平稳信号在分析窗的短时间隔内是平稳的。通过分析窗在时间轴上的移动使信号逐段进入被分析状态，得到不同时刻“局部”频谱图。该算法简洁，是研究非平稳信号常用的工具。在应用中要合理选取窗函数和窗函数的长度，在频率分辨率和时间分辨率中进行合理分配。