空化流场随空化数的不同表现出较为明显的流动形态特征差异，这种差异引起了作用在水翼的流体作用力的不同。在水动力的测量中，应用梁式电阻应变力传感器是一种可行的方法，它具有转换元件体积小、反应快、使用简单、可同计算机配套进行测量等优点。电阻应变片作为传感器中将非电量参数转换为相应的电量参数的最关键部分，利用金属导线的应变-电阻效应进行工作。当应变片粘贴于弹性元件上时，弹性元件受力作用所产生的应变就会传递到应变片上，从而使应变片阻值发生改变，通过测量阻值的改变量，可间接反映出载荷的大小。为了减少传感器灵敏系数随温度变化而发生的改变，应尽量选用栅长较短和较薄的箔式电阻应变片。

图3-1所示为流体水动力测量系统示意图。该系统主要由动态应变仪、电荷放大器以及数据采集系统等组成。选用动态应变仪与箔式中温电阻应变片组成测量电桥，测量被测物体所受的升力和阻力。

图3-1　流体动力测量系统示意图

用于固定支撑轴的侧壁上的孔须足够大，以避免限制测试物体在流体作用下的移动。在实验过程中不进行抽压时，水流容易从柱体与实验段缝隙中喷出，造成大量的泄漏；当进行抽压时，内外压差较大，外部气体又容易进入内部，造成内部压力达不到效果。为此，特别利用高弹性橡胶专门设计了密封套，使其在防漏的同时又不影响水翼的振动。

常用的数据处理方法就是无量纲化，得到流体作用力系数，即升力系数和阻力系数。同时，对测得的流体作用力信号进行谱分析，可以得到流体作用力的频率，进一步计算出汽-液两相斯特劳哈数，它可以表明空泡脱落特性的相似准则数。

升/阻力系数Cl、Cd分别定义如下：

式中，Fx和Fy分别为水翼所受的阻力和升力。

水翼在流体中受到的动力波动主要由两个原因引起：一是流体中的湍流随机波动，其幅值较小，体现于信号中高频部分；二是由于空泡团脱落所引起的，其幅值较大。对动力信号进行频谱分析后，得到的频率谱主频对应的信号集中了大部分能量，对应于空泡脱落的频率，体现于信号中低频部分。由于空化流动的复杂性，同时在测量过程中，外界环境对测试系统所产生的不可避免的干扰，致使动态动力的周期性脉动信号可能淹没在随机振动信号中。因此，首先需要作测量信号的预处理，去除夹杂在有用信号中的噪声信号。对这种信号的消噪，传统的傅里叶变换分析显得无能为力，它不能给出信号在某个时间点上的信号变化情况，使得信号在时间轴上的任何一个突变，都会影响信号的整个谱图。在研究中，将捕捉到的振动信号经过低通滤波，并通过小波分析对测得的动力信号进行消噪。通过降噪可以最大限度地保留原始信号中所关心的低频部分而剔除高频部分。

消噪过程主要分为以下3个步骤：

（1）升阻力信号的小波分解。选择合适的小波并确定一个小波分解的层次N，然后对信号s进行N层小波分解。(www.daowen.com)

（2）小波分解高频系数的阈值量化。从第一层到第N层的每一层高频系数选择一个阈值进行软阈值量化处理。

（3）小波的重构。根据小波分解的低频系数和高频系数，进行信号的小波重构。

对于信号s（t），它的连续小波变换可表示为

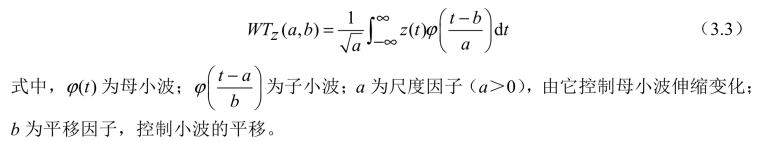
图3-2给出了无空化工况下（σ=1.60），水翼升力信号用dB10小波基函数分解的结果。其中图3-2（a）中第1～第6层是分解后得到的细节信号，图3-2（b）是各层细节信号作希尔伯特（Hilbert）包络，并进行谱分析，获得不同频段升力变化的功率谱分布，图中横坐标是频率，纵坐标是归一化能量。

图3-2　升力随时间变化的小波变换（σ=1.60）

从图3-2中可以看出，得到的各层细节中的信号规则性随着层数的增加而减弱。从功率谱的分析中可以发现，第1与第2层分解信号对应的水翼升力的功率谱图表现为窄带，其他的频率成分是宽带过程，其频谱近似于白噪声谱，可以认为是由外界噪声的高频分量引起的局部干扰。信号中低于频率200 Hz的频率分量能量远小于信号中的高频部分，说明空化数σ=1.60时，水翼升力信号不存在周期性。

图3-3给出了空化数σ=0.96时，水翼升力信号用dB10正交小波基进行6层小波分解得到的结果。从图3-3中可以看出，得到的各层细节中的信号规则性同样随着层数的增加而减弱，第3～第6层小波的功率谱为宽频带，其幅值远小于信号的低频成分。第1和第2层小波的功率谱为窄带谱，比较第1和第2层小波，第2层具有明显的峰值，而且第2层小波能量最大。由此说明，第2层贡献最大，它提取了原始数据曲线的形状，此时第2层小波峰值对应的频率为22 Hz。

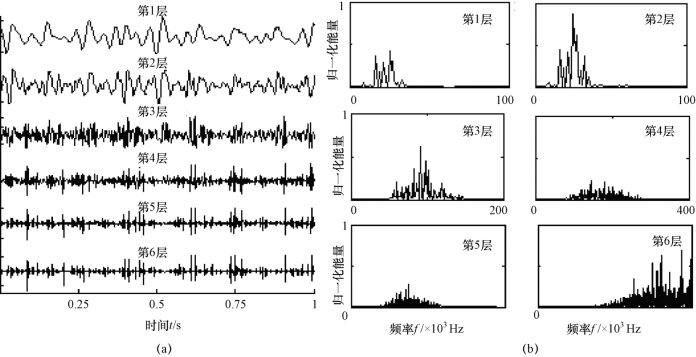
图3-3　升力随时间变化的小波变换（σ=0.96）