曲面造型技术随着数学相关研究领域的不断深入而得到长足的发展，多种曲线、曲面被广泛应用。我们在此主要介绍其中最基本的一些曲线、曲面的理论及构造方法，使读者在原理和概念上有一个大致的了解。

1．贝塞尔（Bezier）曲线与曲面

Bezier曲线与曲面是法国雷诺公司的工程师Bezier在1962年提出的一种构造曲线曲面的方法，是三次曲线的形成原理，这是由四个位置矢量Q0、Q1、Q2、Q3定义的曲线。通常将Q0、Q1……Qn组成的多边形折线称为Bezier控制多边形。多边形的第一条折线和最后一条折线代表曲线的起点和终点的切线方向，其他曲线用于定义曲线的阶次与形状。

2．B样条曲线与曲面

B样条曲线继承了Bezier曲线的优点，仍采用特征多边形及权函数定义曲线，所不同的是权函数不采用伯恩斯坦基函数，而采用B样条基函数。

B样条曲线与特征多边形十分接近，同时便于进行局部修改。与Bezier曲面生成过程相似，由B样条曲线可以很容易推广到B样条曲面。

3．非均匀有理B样条（NURBS）曲线与曲面

NURBS是Non-Uniform Rational B-Splines的缩写，表示非均匀有理B样条。具体解释是：

Non-Uniform（非均匀）：指能够改变控制顶点的影响力的范围。当创建一个不规则曲面的时候，这一点非常有用。同样，统一的曲线和曲面在透视投影下也不是没有变化的，对于交互的3D建模来说，这是一个严重的缺陷。

Rational（有理）：指每个NURBS物体都可以用数学表达式来定义。

B-Spline（B样条）：指用路线来构建一条曲线，在一个或更多的点之间以内插值替换。

NURBS技术提供了对标准解析几何和自由曲线、曲面的统一数学描述方法，它可通过调整控制顶点和因子，方便地改变曲面的形状，同时也可以方便地转换成对应的Bezier曲面，因此NURBS方法已成为曲线、曲面建模中最为流行的技术。STEP产品数据交换标准也将非均匀有理B样条（NURBS）作为曲面几何描述的唯一方法。

4．NURBS曲面的特性及曲面连续性定义(www.daowen.com)

（1）NURBS曲面的特性。

NURBS是用数学方式来描述形体，采用解析几何图形，曲线或曲面上任何一点都有其对应的坐标（x,y,z），所以具有高度的精确性。NURBS曲面可以由任何曲线生成。

对于NURBS曲面而言，剪切是不会对曲面的UV方向产生影响的，也就是说不会对网格产生影响，如图1.2.1所示。剪切前后，网格（U方向和V方向）并不会发生实质的改变，这也是通过剪切四边面来构成三边面和五边面等多边面的理论基础。

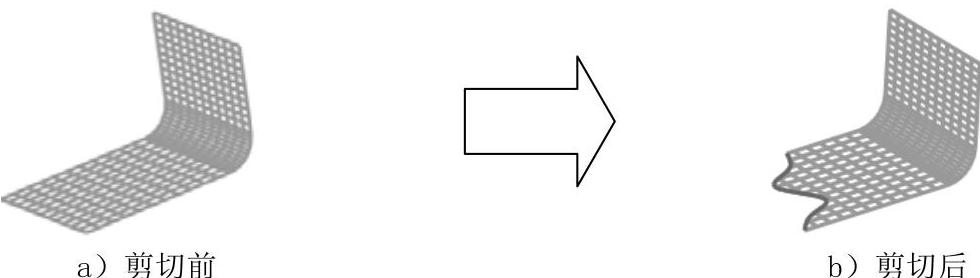
图1.2.1 剪切曲面

（2）曲面G1与G2连续性定义。

Gn表示两个几何对象间的实际连续程度。例如：

G0意味着两个对象相连或两个对象的位置是连续的。

G1意味着两个对象光滑连接，一阶微分连续，或者是相切连续的。

G2意味着两个对象光滑连接，二阶微分连续，或者两个对象的曲率是连续的。

G3意味着两个对象光滑连接，三阶微分连续。