由于短的影像获取时间间隔（9分钟），因此，可以忽略坡体介电常数和大气延迟的影响，但是对于突变的天气变化，大气延迟的影响是不能忽视的。得到的差分相位可以依据式（13.2）直接转换为视线方向的形变量：

图13-11为一个时间序列的8幅差分后形变图像，时间范围为37小时。形变方向对应着坡度在视线方向的移动，负值表示距离减小，即朝着观测者运动。从图13-11可以看出，观测20小时之前，整个坡体保持稳定，没有明显的形变区域，20小时后，坡体左上角有一个区域出现明显形变，形变区域由中心向外围扩展。图中其他区域也存在零散的形变比较大的点，这是由于SAR影像受到斑点噪声的影响造成，因此，仅考虑影像间的相干性选择高质量点是不完整的。

图13-11　2010年09月12日15：33至2010年09月14日06：26获得的形变

为更详细地了解形变区域的运动过程，对形变区域做了时间序列分析，选择区域如图13-10所示，对形变区域内所有点的形变量取均值作为区域形变值，可以看出形变量和形变速度都表现出明显的线性趋势，依据形变值得到区域性形变和形变速度图像，如图13-12所示，从图可以看出此区域在40小时的监测中，总体形变值为5.08mm，基本保持-0.026mm/h的形变速度。同时采用前30小时内的形变值做拟合值进行线性回归分析，求出形变方程，后10小时的形变值检验拟合精度，拟合中误差为0.081mm，小于地基合成孔径雷达干涉测量的精度（0.1mm），因此，拟合的线性形变方程是可靠的，可以预测形变值。采用相同的方法拟合了线性形变速度方程。

图13-12　主要形变区域的位移和位移速度时间序列图(www.daowen.com)

对形变区域安置棱镜的3个点也做了时间序列分析，图13-13~图13-15为各点的形变和形变速度图像，从图中可以看出，点1、点2、点3三点都表现出线性的形变趋势，但是与区域形变趋势相比，个别时刻存在异常形变值，因此不能采用普通的线性回归分析，再用两种措施拟合线性形变趋势，分别为抗差线性回归分析和时间维低通滤波后线性回归分析，通过比较分析，两种方式都能去除粗差点的影响。地基合成孔径雷达干涉测量的是视线方向的形变值，而全站仪观测得到的是垂直方向的形变值，依据雷达成像的几何关系，虽然可以把视线方向的形变量分解为垂直方向的形变量，但是由于坡体地形的复杂性，得到的垂直方向的形变量存在不确定性，因此，二者得到的结果不可能完全吻合，从图形可以看出，此案例得到的结果基本保持吻合，最大的差值为0.5mm。从3个点分布的位置可以看出，点1位于形变区域中心，在40小时监测时间段中，形变值较大，达到6.95mm，其次为点2和点3，分别为6mm和4.79mm；3个点的形变速度依次为-0.029mm/h、-0.022mm/h和-0.016mm/h。测量结果也可以评定地基合成孔径雷达干涉测量监测边坡的精度，对于区域形变监测精度约为1.5mm，单点精度为1.7mm。由于区域形变值是由形变区域形变值平均得到的，故形变监测精度略高于单点精度。

图13-13　点1的位移和位移速度时间序列图

图13-14　点2的位移和位移速度时间序列图

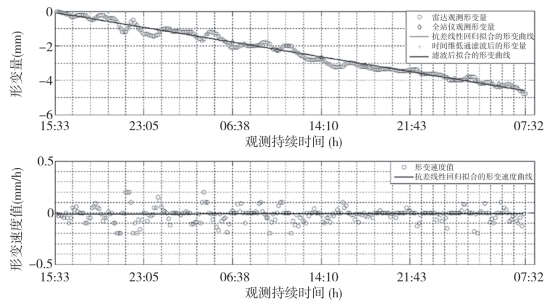
图13-15　点3的位移和位移速度时间序列图