为验证二次曲面大气相位改正法的效果，以某稳定的城市建筑区为监测区域，进行监测分析。从图7-7可见，建筑物在雷达波束照射下具有较强的反射信号，大部分监测区域的信噪比在35dB以上，实验根据数据相干情况且顾及PS点的分布，设定相干阈值γ＾＞0.9和振幅离差指数＜0.2，从连续监测影像中提取了3938个PS点（见图7-8）。图7-9显示了提取的PS点在极坐标下的分布，可见提取的点位分布比较均匀且密度适中。构建Delaunay三角网以检核边网稳定性，共生成了7859个三角形，但是其中有较大边长组成的狭长三角形。数据处理中设定边长阈值为20m，将大于此阈值的三角形从三角网中去除，小于此值则保留。经计算，一共剔除了248个含有大于20m边长的三角形，最终得到的检核三角网如图7-10所示。

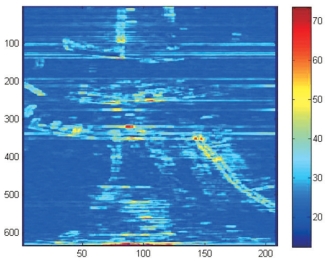
图7-7　监测区域的信噪比（SNR）图

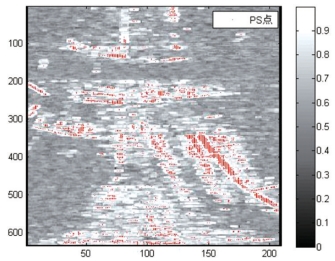
图7-8　双阈值法提取的PS点分布

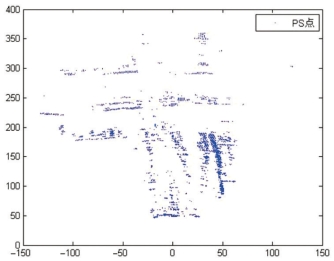
图7-9　极坐标下的PS点分布

图7-10　三角网网边稳定性检核(www.daowen.com)

对剔除“奇异点”后的PS点进行空间解缠，得到解缠相位结果如图7-11所示。由于观测的时间基线长达4h，空气中的温度湿度具有一定的变化，因此，解缠后的形变相位主要是大气成分。利用上节提出的二次曲面拟合公式，通过最小二乘迭代求解多项式系数，再经Kriging可以得到每个像元上的大气相位进而得到整幅影像的大气相位屏（APS）（见图7-12）。图7-13描述了所有PS点经过大气改正的结果，可以看出相位结果准确地体现了监测区域建筑物自身的稳定性。为更加直观地分析大气改正的精度，将经过大气改正的所有PS点的相位进行直方图统计（见图7-14），可以看出改正后的形变相位主要在±0.5rad区间内，该相位值对应的视线向形变仅为0.7mm，证明基于二次曲面拟合的大气相位屏提取方法是可靠的，GBSAR观测数据中的大气扰动误差得到了有效的改正，最终取得了较为满意的监测结果。

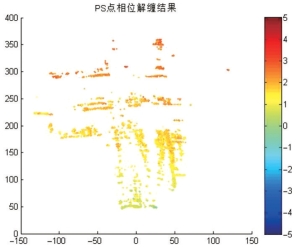
图7-11　PS点空间解缠结果（rad）

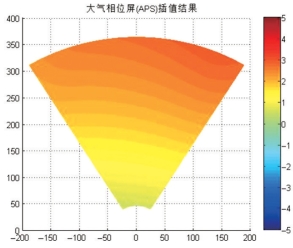
图7-12　基于Kriging插值的APS（rad）

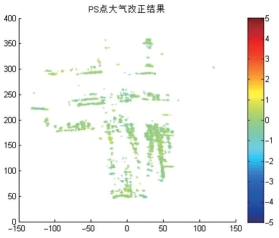
图7-13　经大气改正后的相位结果

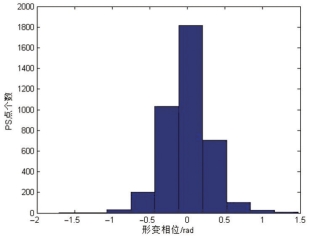
图7-14　大气改正后的相位直方图