由大气相位的分布规律可以得知，大气相位的改正不是简单的线性关系，而是一个多元线性拟合问题。影响大气相位分布的折射率是二维分布的，且在空间上具有一定的相关性，因此，可以通过曲面拟合方法来重建采样时刻的大气相位屏。

GBSAR进行长时间连续监测时，干涉相位中大气误差容易累积从而影响监测精度，不利于长期监测。在充分顾及大气相位二维分布规律的基础上，提出大气相位屏提取方法来改正主辅影像间的大气误差。在估算出稳定区PS点的大气相位值后，经插值得到的整个监测区域大气相位分布的过程，称为大气相位屏提取。具体的处理步骤如下（参见图7-6）：

（1）地基SAR数据采集。对于监测区域，选择合适的雷达视角及相关参数进行连续观测。选取具有一定时间间隔的两影像为主辅影像，得到它们的单视复数影像阵分别为M和S，对应的相位阵则分别为ΦM和ΦS。

（2）幅值定标。由于PS点的提取需要基于幅度的统计特性，因此要将时序影像进行幅值定标。将时序SAR数据的幅值统一在一个尺度下，能够提高PS点的提取精度。

（3）PS点提取。PS点提取方法是基于数学统计特性的，因此，连续观测的影像最好不要少于30景。利用振幅离散指数与相干性双阈值进行PS点的提取，阈值的选择要依据PS点提取的密度与分布情况适当进行调整。

（4）干涉处理。对主辅两影像进行差分干涉处理，得到干涉相位阵ΔΦ＝ΦS-ΦM。利用PS点对应的点位信息，建立PS点干涉相位集ΔΦPS。由于此时的干涉相位是缠绕相位，其范围在（-π，π]内，不是真实的形变相位，因此需要进行解缠。

（5）空间二维解缠。选择合理的解缠起算点后，利用质量图引导法对离散的PS点进行空间二维解缠，获取准确的缠绕模糊度，得到真实的干涉相位信息。由于这里仅对一组干涉对提取大气相位，因此无须进行三维解缠处理。

（6）选定稳定区。由于只有监测区域内稳定区的相位形变才是大气相位造成的，如果将非稳定区加入曲面拟合过程，则会严重影响反演大气相位的精度。因此，在进行大气改正前，依据先验知识选定稳定区，避免非稳定区的PS点进入大气拟合过程。

（7）构建Delaunay三角网。依据先验信息得到的稳定区域，无法保证所有区域内的点仅受大气影响，因此需要进行逐个的筛选和甄别。可以通过构建Delaunay三角网，利用边长阈值去除狭长三角形后计算邻接顶点的干涉相位差Δφ″。由于大气相位在空间具有相关性，因此可以利用Δφ″＜1.5rad来判断三角网内是否有“奇异点”，当大于某设定阈值则视为“奇异点”，用三角形内其他顶点的干涉相位均值代替此点相位值。(www.daowen.com)

（8）二次曲面拟合提取大气相位屏。对于稳定区大气相位的二维分布则可利用式（7.20）来拟合：

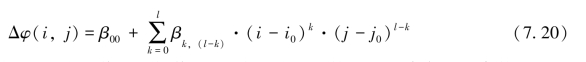
式中，（i，j）表示PS点的像元坐标值，β为多项式的系数，也是待求解的参数，（i0，j0）表示曲面拟合坐标系的指定原点。由地基干涉模型公式可知，此时稳定区PS点集的干涉相位，主要含有大气成分和少量噪声，且大气成分占主要部分。可将PS点干涉相位作为观测值Δφ代入式（7.20）中，利用最小二乘拟合得到多项式系数初始估值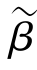。根据计算得到的残差评估该点得到的大气相位精度，如果残差大于0.36rad（该大小对应的视线距离约为0.5mm），则去除该点后重新进行最小二乘拟合。由于具有Delaunay三角网边网稳定性检核，迭代次数一般不超过3次即可得到满意的拟合精度。

（9）基于Kriging插值得到大气相位屏。利用稳定区PS点的大气相位，通过Kriging插值法估计出对应于每一景雷达图像中每一个像元的大气相位，即大气相位屏（APS）。插值公式为：

式中，APS（si）为第i个PS点的大气相位，s0为未知像点位置，si为已知像点位置，M为估算大气相位值所需的PS点个数，λi为距离反比加权函数，表达式为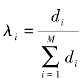，式中di为待估像点与PS点的距离值。最后利用APS去除干涉相位ΔΦ内所有的大气相位成分。

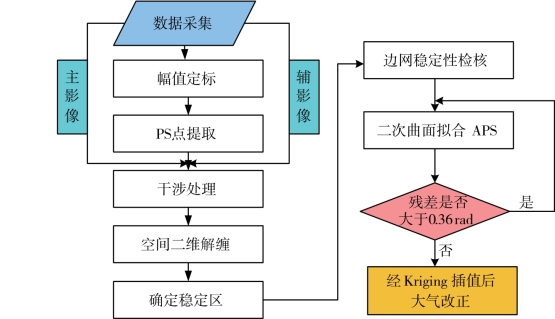
图7-6　GBSAR大气相位改正流程图