大气扰动函数可表示成距离的函数：

式中，A（t）和B（t）为与时间相关的常数。目标点的干涉相位可表示为：

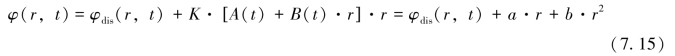
式中，a和b为随时间变化的系数。

通过两个已知的固定点R1和R2的差分相位可求得a和b的估值：

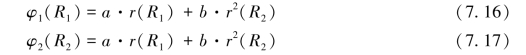
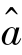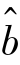利用估值和改正其他任意目标点的差分相位：

最后，可由改正后的差分相位计算目标的位移值：(www.daowen.com)

二阶改正模型可用于气象条件变化明显的较大区域。

选取主辅影像后，对它们进行干涉处理，获取干涉图如图7-3所示。根据信噪比或相干性等阈值提取了固定点GCP1和GCP2，为达到较理想的改正结果，特别选取近雷达端固定点为GCP1，远雷达端固定点为GCP2，固定点相关参数可参见表7.3。固定点改正法的核心思想是利用式（7.2）提取固定点上的折射率n，利用其与斜距间的线性关系来改正整幅干涉相位。从表7.3中计算的两点折射率可以看出，两固定点折射率不完全一致，因此在多点固定点进行改正的时候，常取折射率差均值进行改正。

通过将所有PS点根据折射率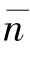来解算大气相位进行改正后，所得到的结果如图7-4所示。可以看出，由于固定点法仅利用空间上极少量的点来替代大气相位，无法顾及大气相位曲面分布特性，因此容易出现对于临近控制点区域大气改正效果好，但是远离控制点区域比较差。并且由于固定点法缺少选取的标准，随机性较大，容易将自身的相位误差引入计算过程中，改正结果缺乏稳定性。从图7-5的改正相位直方图中可以看出，由于对提取PS点内没有进一步的处理机制，往往会出现较大的偏差。虽然大部分相位改正在±1rad区间内，但也有部分改正出现在-6rad左右。因此可知，固定点法大气改正难以进行大气相位高精度的去除，受选点和无PS点检核条件等的限制，对局部区域有明显效果，但对于大范围的监测来说，易出现较大的改正偏差。

图7-4　固定点法大气改正结果

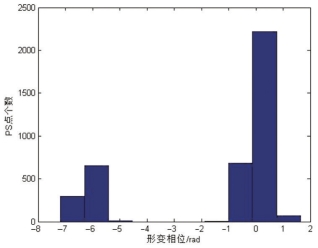
图7-5　固定点法改正结果相位直方图

表7.3　固定点相关参数