由地基SAR干涉测量误差分析可知，若主影像相位为φM，而从影像相位为φS，则干涉相位模型为：

上式中存在有形变相位、大气扰动相位以及噪声相位。对于地基SAR变形监测有重要作用的，仅仅是其中的形变相位部分，因此从某种意义上讲，地基SAR干涉测量方法类似于星载InSAR，都是将有用的相位成分从无用的相位成分中一步步剥离的过程。

在分离出形变相位信息前，有必要了解形变信息的特征。利用合成孔径雷达干涉测量方法进行变形监测，通常是基于一定的假设前提的，即目标区域的形变相对于采样间隔是缓慢的。这一假设在实践中也得到了验证，以IBIS-L的采样时间间隔平均为6min为例：间隔内1.5rad的相位形变就会带来504.2mm/d的形变速率，3 rad的相位形变则产生近1m/d的形变速率。这种情况在实际的变形区域中是极少出现的，但在干涉处理过程中，由于二维空间解缠存在错误或去相干的影响往往会出现这类错误（如图6-6所示）。因此时序一维解缠实际上就是利用一定的准则与方法，校正这类错误或剔除一些相位质量非常差的PS候选点，以确保相位在空间和时间上的准确性。

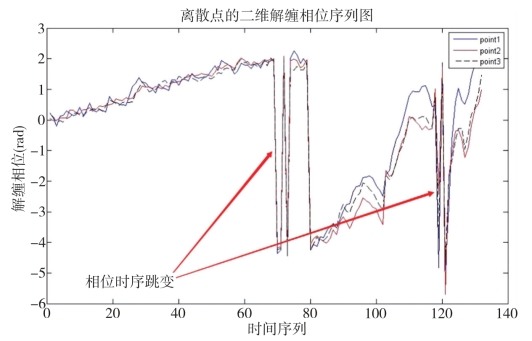
图6-6　二维解缠错误产生的时序跳变

为了剔除此类错误，需要对空间二维解缠后的时序相位进行处理。式（6.14）左边为实际的观测值，未知数则为主从影像相位。如果假设初始相位时刻的相位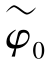＝0，则时序上相位估值应该满足：

即第i幅时序解缠相位应含有该时刻的形变相位与大气相位成分（相对于初始时刻），因此，N幅影像构成的N-1个干涉方程则未知数亦为N-1个，这是因为假设前提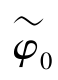＝0。那么估值与观测值间的差值则为残差：(www.daowen.com)

每个像元若仅有N-1个干涉相位，则方程只有一个解，无法对估值精度进行评价，因此通常可以利用类似于短基线干涉测量（SBAS）的方法建立冗余观测方程来增加干涉方程的个数。

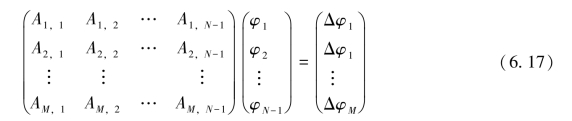
式（6.17）表示冗余干涉方程，式中M为冗余方程个数，一般是邻近的不小于3个SAR影像进行两两干涉，可见M≪N；冗余系数矩阵为A，矩阵内每个像元均由1、-1或0组成；式中Δφ1，…，ΔφM为观测值，最终得到解缠相位的最小二乘估计值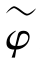，…，。通过最小二乘法奇异值分解（SVD LS）的方法得到相位估值，利用残差评定估值精度，大于阈值则进行解缠处理，满足阈值则视为准确估值。时序相位解缠的过程是一个循环迭代的过程，最终获取整体残差最小的解缠相位估计值。该算法的具体步骤如下：

（1）对每个像元的干涉相位，根据式（6.14）建立时序干涉方程，利用SVD LS求解第一组相位估值。

（2）设定残数最大阈值，本书设定此值为3rad，如果相位估值对应的残数大于3rad则将此点划为“PS待定点”。

（3）将暂时剔除“PS待定点”后的干涉方程组，进行新的最小二乘估计。

（4）检核“PS待定点”，如果残数为2π的整数倍，可以对残数取余。若余数小于可接受阈值Δtoler，则可将此点相位解缠后继续加入干涉方程组，否则剔除，本书设定该阈值为0.3rad。

（5）检核后，对新的干涉方程进行新最小二乘估计，重复迭代（2）至（5）步骤，直到方程收敛获取最优的相位估值。