1.最小二乘解缠法

最小二乘是一种全局最优的解缠方法，实际上是寻找基于最小化范数的相位解缠算法，通过使真实相位梯度和缠绕相位梯度的差异最小来实现全局最优。Ghiglia和Romero于1996年提取最小范数框架来描述这一思想，并提示了很多算法间的理论联系，包括上文所述的路径积分算法。在此框架下，相位解缠被视为最优化问题，优化目标为：

式中，Δφ和ΔφM为真实相位梯度与缠绕相位梯度，优化目标就意味着它们之间的差异最小。q是自定义权重，r和a分别代表着距离向和方位向。当p取不同值时，对应着不同的范数作为优化标准。当p＝2时，对应的则是最小二乘法相位解缠。

Ghiglia和Romero在Fried，Hudgin和Hunt等人工作的基础上，认识到在二维相位场中最小二乘算法实质上就是求解Neunmann边界的泊松方程：

∇2为拉普拉斯算子，为真实相位场的估值，表示缠绕相位梯度的微分，Ψ表示缠绕相位场。通过FFT或DCT可快速求得无权重的最小二乘解。

但是这类算法不检测残数点，不关心相位是否连续，因此，最小二乘解无法保证解缠相位与缠绕相位相差整数个2π周期，从而会破坏相位主值。它仅能够保证解缠相位梯度与缠绕相位梯度之差平方和最小，不能保证每个像元解是正确的。因此常引入权重来弥补以上缺陷，权重可由相干图等先验知识来确定。加权后的最小二乘不再适用泊松方程的求解条件，Ghiglia和Romero虽然提出通过迭代运算来趋近于加权最小二乘解，但计算效率大大降低了。当p＝1时，对应的则是最小费用流的相位解缠方法。

2.最小费用流（M inimum Cost Flow，MCF）(www.daowen.com)

最小费用流法可将相位解缠转化为线性的最优化问题的求解，通过图论和网络规划算法来解决这一问题，并且计算效率较高。基于以上思想，Costantini于1998年提出了最小费用流算法。

MCF算法允许将质量参数作为费用函数加入费用流的统计中，并且该算法能够得到解缠相位与缠绕相位整数个2π周期的解决方案，从而保护了相位主值不受破坏。假设一个非0的费用函数Ci，j，将每个边（i，j）限定整数个相位周期，则将二维相位解缠问题转化为如下式的费用优化问题：

式（6.12）中，估计真实相位梯度就变成了求解整数Kij，为满足积分与路径无关条件，则对于矩形的闭合角点A，B，C，D来说，必须满足：

上式为此费用函数的约束方程，其数值等于图6-5中每个闭合环对应的残数，式（6.12）中‖·‖表示L1范数，E表示闭合矩形格网的各边。最小费用流是指使网络中总费用最小的流的集合，且总的输入流等于总的输出流，在每个节点上输入流和输出流也是相等的。求解这样一个最小费用流就相当于求解一个与积分路径无关的解缠相位场，问题最终成为在变量为整数的线性费用网络中寻找总费用最小的可行流。网络规划中常用的松弛算法和网络单纯形法可高效解算这一问题。最小费用流可以得到全局L1范数解，但由于过分地强调全局最优解，从而解缠相位会在相干性好的地方丢失较多细节以照顾相干性差的地方。其原因在于基于Lp范数的框架只是抽象的数学量，通过它可指导相位解缠，并不能保证求得正确的解。

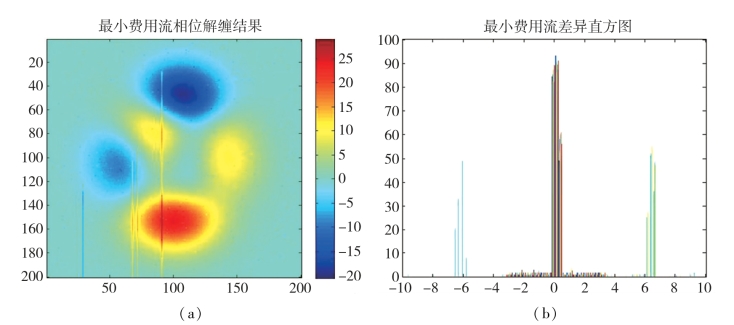
图6-5　最小费用流相位解缠结果和差异直方图