1.枝切法（branch cut）

Goldstein在1988年提取了经典的路径积分算法——枝切法，此算法用2×2像元形成的最小闭合路径积分检测出二维相位数据中的所有残数点，用枝切使得所有的积分路径不包含未平衡的残数点（积分路径内所包含的残数点的残数和为零）。

在图6-3（a）中，检测出两个残数点，其残数值分别为+1和-1，用枝切将这两个残数点连接起来，如图6-3（b）中黑线所示；对相位梯度进行积分时，积分路径不可穿越此枝切，在这种情况下任意闭合路径所包含的残数值为0。于是枝切法就是将所有的残数点用枝切连接起来，形成多个树状枝切，并且保证每个枝切树所连接的残数点的残数和为0；连接残数点的枝切表示相位不连续地方，阻止积分路径从这些地方穿过，避免出现整周跳变和二维相位场的不一致。

在设置枝切时，其原则是使枝切的总长度最短，即干涉图中相位不连续的总长度最短。在图6-4（a）中，黑白色的点分别代表正负残数点，图6-4（b）中的枝切设置显然是不合理的，会出现不连通的区域无法积分解缠，图6-4（c）中的枝切设置是较为合理的。

图6-3　枝切法解缠示意图（图中数值需乘以2π）

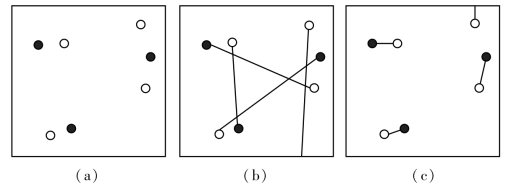
图6-4　枝切的连接方法示意图

枝切法解缠的计算速度快，解缠相位与缠绕相位只会相差2π的整数周期，不会破坏真实相位的主值；但是最大缺点就是当干涉图相干性较差时，可能得不到一个完整的解。在相干性高的区域，其解缠结果是准确的，但在低相干区，残数点密集区，很难正确地设置枝切，常得到不准确解，甚至枝切会形成许多孤立区域，这些区域是无解的。(www.daowen.com)

2.质量图法（quality guided path follow ing）

枝切法中切线的连接实际上是很复杂的，组合方式会很多，难以判断哪一种结果是最佳选择。因此，有必要引入其他信息来辅助解决这些问题。质量图引导的路径跟踪算法，就是基于这种思路的二维解缠方法。其特点是：利用质量图引导解缠路径不会环绕残数点，积分路径不依赖枝切线。

质量图法的解缠过程类似洪水漫淹，但漫淹的顺序是由质量图来引导的。该方法的基本步骤如下：

（1）按照某一准则（相干性或相位梯度）生成一幅质量图，这样干涉图中每个像元都对应着一个干涉质量标识。

（2）以某一高质量的像元为起点，遍历其邻接像元，将它们解缠后并存入“邻接表”（adjoin list）的数组中。

（3）在邻接表所列出的相邻点中选出一个质量最高的像元，将这个像元从表中删除，将其解缠后并把该像元的相邻像元加入邻接表。

（4）重新将表中各像元按质量排序，如此迭代方式进行下去，逐渐扩大已解缠区域，直至质量最差的像元。

质量图法采用枝切线来避开残数点，但需要依赖干涉质量指标。产生和不断地更新这个邻接表，在计算中占用很大的内存空间和运算时间。通常会采用一定阈值限制过多像元进入邻接表中，高于此阈值加入表，低于此阈值的像元则推迟加入。解缠初始时，阈值可设定较高，在计算过程中逐渐降低，最后解算所有像元的模糊度。