由一定条件下通过相位梯度积分，来实现一维相位解缠的思想出发，二维相位解缠可由对相位梯度的路径积分来完成：

其中∇φ为相位梯度，C为连接r0和r的任意路径。根据微分学，线积分的结果取决于起点和终点，但与路径本身无关。但在实际情况下，干涉图不一定满足Nyquist采样定律，从中提取的缠绕相位场存在大量的相位不连续。需要避开的这些区域，往往都存在相位的不一致，是沿着环绕二维的某一区域的闭合路线对缠绕相位差进行积分时，沿不同路径的积分结果不同。也就是说解缠结果实际上与路径有关。所幸的是，这种不一致的现象总会发生在一些孤立的点或小的区域上。

Goldstein等（1988）发现这些相位不一致的区域，能够通过相位梯度环绕求和不为0来标识出，称之为残数（Residue）。如图6-2所示，闭合环路中残数+1和-1由残数公式可以计算得到，将残数标定于对应环路的中心，这个过程称为残数探测。(www.daowen.com)

积分时通过这些地方会引起全局的解缠误差，故积分不完全与路径无关，因此积分时要利用行、列方向上相位梯度的相关性避开这些地方。基于以上思想的解缠算法称为路径积分算法，其本质是选择一条适当的积分路径。

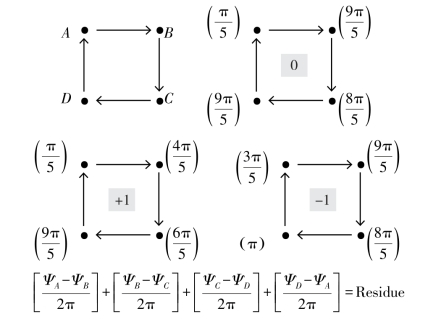
图6-2　残数探测示意