假设一维方向上一个复数信号为：

其真实的相位信号是：

经式反正切提取相位主值运算后，会将真实的相位信号缠绕，结果如图6-1所示：

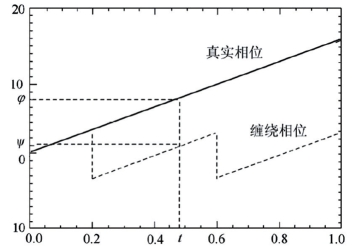
图6-1　一维相位解缠原理

缠绕相位ψ呈周期性变化，当真实相位值大于π时，缠绕算子w会将其缠绕至区间-π，π（]内。图6-1揭示了一维缠绕相位与真实相位间的对应关系。

假设一维的相位采样满足采样定理，即相邻像元间的相位差绝对值小于π，图6-1中时间刻度间距为Δt＝0.05，则两相邻相位对应的真实相位差的绝对值为＝5πΔt＝0.25π＜π，离散的缠绕相位信号与真实相位间的关系可表述为：

上式中i为样本序号，N为样本数。定义差分算子Δ为：(www.daowen.com)

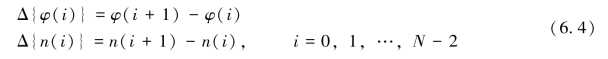
利用上式对缠绕相位作差分运算可得到：

再对上式进行缠绕算子运算一次，则有

式中n1和n2用来表示两次作缠绕运算时的整数序列。因缠绕运算w{Δ{ψ（i）}}所得到的结果必然在区间-π，π（]内，即-π＜Δ{φ（i）}≤π。因此2πΔ{n1（i）}+2πn2（i）必须等于0才能同时满足这两个条件。则式（6.6）可写为：

通过对缠绕相位ψ的差分缠绕值进行积分，即可得到真实相位：

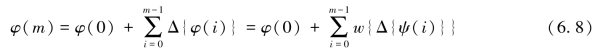
由上式可知，如果对于缠绕相位的差分结果进行缠绕运算后再求和，则可以得到干涉图所包含的真实相位。所有的计算都是基于相邻像元间的相位差绝对值小于π，但是因噪声存在、相位混叠等情况，很可能这一假设无法满足，因而一维的情形下，从解缠相位中重建真实的相位值几乎是不可能的。当该解缠思想扩展到二维数据时，行、列方向上相邻像元间的相位差分值不再是独立的，它们之间可以避免一维解缠时出现的错误——因相位不连续而造成的整周跳变。为避免此类解缠错误，就需要寻找合适的路径对相位梯度进行积分，或者利用真实相位梯度与缠绕相位梯度差异最小的方法。