大气扰动改正、相位解缠处理之后得到真实相位，可由此求解位移值。为将GBSAR监测的高精度形变量应用于工程实践，进一步由系统工作的几何关系完成坐标系的转换，并将雷达测得的形变值投影为形变真值。GBSAR系统的工作模式灵活，需根据具体几何关系选取位移解算模型。雷达的几何关系常被分为两种模型，即平行近似几何关系与精确几何关系，在坐标的归化过程中，由观测区域实情和具体精度要求进行取舍考虑。

由星载雷达进行变形监测实验时，测得的变形值近似视为变形的真量，而GBSAR所采用的弹性工作模式，与星载的几何关系存在差异。地基雷达采用的几何原理主要分为两种情况：平行近似几何模型、精确几何模型，具体如图5-2所示。

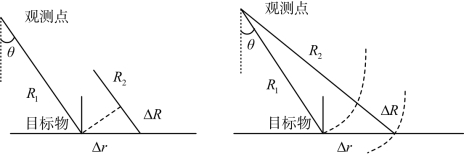
图5-2　平行近似几何模型的空间关系和精确几何模型的空间关系

将雷达和监测目标间的距离与形变值进行对比，两者的差值较大，可将雷达波视为近似平行的关系。设目标的相邻两次观测所得斜距长度分别为R1，R2，将形变真值表示为Δr，雷达入射角用θ表示，视向形变值用ΔR表示。

由几何关系推导可知，变形基于近似平行模型的距离可表示为：

对精确几何模型进行求解，根据余弦定理求得：

式中，形变真值Δr为自变量，对含有该自变量的一元二次方程求解形变真值可得：(www.daowen.com)

上式中，由斜距Δr、视向的实测形变值ΔR和雷达波速入射角θ共同决定了形变真值。视向形变值在目标物形变方向垂直于雷达入射波的情况下取零，雷达系统监测失去了实际意义。

对平行近似模型进行分析，将其误差表达为：

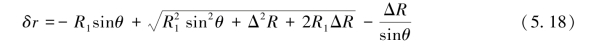
假设目标视线向形变值ΔR＝0.01m，斜距R＝30m，则可得形变真值近似计算误差与雷达入射角θ之间的关系。若雷达入射角θ较小，近似几何模型所带来的误差约为毫米级，与GBSAR的亚毫米级监测精度相比，是不可忽略的影响。

精确几何模型在使用过程中，所获得的形变真值受到斜距长、雷达信号的入射角以及LOS方向的形变值共同作用，且上述自变量之间相互独立。误差均方根可评估出各因素对形变真值的影响程度，对上式中的自变量R1，ΔR，θ分别求取微分，则可得到形变真值与斜距、LOS上的形变值、雷达波速入射角间的敏感函数：

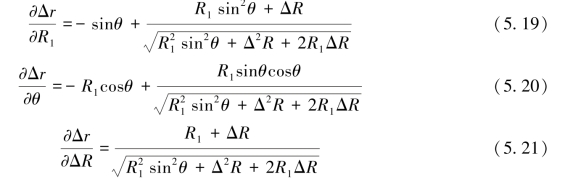
通过研究中的分析可证明，斜距变化对变形观测值造成的干扰较小；角度的影响约为毫米级别，且角度值越大，其变化带来的影响越小。

在利用GBSAR进行实时测量过程中，应对视线向（LOS）的形变值进行处理，解算出目标物安全状态评估时需要的方向上的形变真值。在根据成像平面所包含的位移信息来求取地距平面内的位移信息的过程中，解算所用模型也将对位移精度造成影响。为降低解算误差，获取高精度监测结果，应保证斜距长度、雷达入射角等观测参数的精度，并优先选择精确几何模型来解算位移值。

除此之外，在GBSAR的图像配准、插值等过程中，模型、算法的不完善也将导致相位去相干。GBSAR复图像的高精度配准、数据处理算法的完善，也是GBSAR测量精度影响因素中有待进一步深入研究和解决的关键问题。