成像就是针对场景区域目标的某一特性给出其二维图谱。光学成像是对图像场景中目标材质的光学反射系数分布的显示，而雷达成像则是对成像场景中目标电磁散射系数分布的显示。雷达系统通过信号调制装置产生离散的频域采样信号，而通过调整目标与雷达的相对方位关系得到离散的空间采样。假设g（x，y）是成像函数，由目标位置（x，y）唯一确定，GBSAR自由空间离散频率下的基本成像方程可以用式（3.11）描述。

式中，x，y分别是目标分辨单元在雷达二维平面坐标系中的横坐标与纵坐标，r则是目标到雷达中心的斜距。θ是目标偏离雷达波束中心线的偏角，不同的目标位置即对应不同的偏角，G（f，θ）是在频率f空间位置θ处的回波信号采样。基本成像方程适用于各类离散空间和离散频域采样下的成像，其成像精度由空间和频率各采样值的测量精度决定。下面介绍适用于GBSAR的三种基本成像算法。

1.波阵面后向传播算法

波阵面后向传播算法（Wavefront Back-propagation Algorithm）是雷达成像方程的直接应用，根据参数域的不同可以分为频域波阵面后向传播算法和时域波阵面后向传播算法，该成像算法的具体思路如下。

假设二维平面上一个孤立点目标P，它在以雷达为中心的极坐标系下的坐标是P（ρ，θ），在线性雷达阵列上获取的P点的后向散射信号是G（f，xa），f是信号的频率，xa是雷达天线在导轨（或线性天线阵列）上的位置。假设后向散射信号是在时域和频域里的一致采样信号，xa和f都在均匀地按照一定步长发生变化，那么我们可以得到如下一个复数二维矩阵：

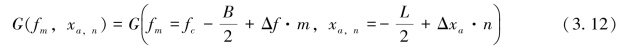
式中，m＝1，2，…，M-1；n＝1，2，…，N-1；fc是雷达中心频率；B是雷达信号带宽；f是频率变化步长；M是频率变化总数；Δxa是天线阵列单元间距或者是天线在线性导轨上位置变化的步长；N是天线阵列单元总数或者天线在导轨上的位置总数。

通过连续累加在不同天线位置、不同信号频率的回波信号，从而得到雷达影像。

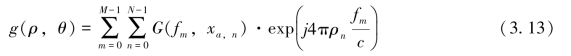
式中，c是光速，

利用式（3.13）成像的计算非常耗时，其时间复杂度是O（MNM＇N＇）。M＇和N＇分别是y和x方向的分辨单元数。该算法是波阵面后向传播法的频域形式，相应地有时域波阵面后向传播算法。相比于频域形式，时域波阵面后向传播算法计算效率高，其成像公式如下所示：

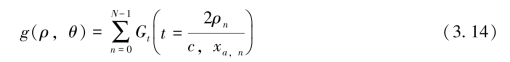
式中，Gt（t，xa）是时域的散射回波数据，其计算的时间复杂度是O（NM＇N＇），当计算的目标不是整幅影像时，计算时间的复杂度则可高效地降低为O（NJ）。时域波阵面后向传播算法在近场和远场的成像具有相同的进度，计算量也较大，通常作为评价其他算法的参考。

2.极坐标格式化聚焦算法

极坐标格式化聚焦算法（Polar Format Focusing Algorithm）源自光学信号处理，也被称为距离-多普勒算法（Range-Doppler Algorithm）。该算法基于频域后向散射数据的极坐标分布性质，通过对信号用极坐标格式记录来消除距离徙动的影响。由于该算法仅对视场中某一点进行运动补偿，通常适用于远场成像。其成像基本公式由二维傅里叶变换构成，可以应用FFT算法，但在傅里叶变换之前需要进行插值计算，而且对距离弯曲只是进行了部分补偿。最初是为星载、机载SAR成像设计，在一定约束条件下仍然可以运用到GBSAR的成像中。由于对某一个点（通常为影像中心点）进行运动补偿，影像宽幅需要小于雷达到中心点的距离，从而尽量减小聚焦影像中除中心外的其他点产生的几何畸变。由于算法的限制，最终聚焦影像中仍会存在一定的几何畸变，而且随着影像宽幅的增大，畸变会越发严重。极坐标格式化的基本思路是对目标后向散射回波信号数据的存储格式进行修正，如图3-5所示。首先，对影像中心点进行运动补偿，完全消除该点的距离弯曲影响。再在距离向和方位向进行插值（即按照极坐标系进行格式化）以减少中心点以外各点处距离弯曲残差。在距离向进行加权处理并计算FFT，此时应用自聚焦算法减少运动补偿和数据格式化过程的相位误差，再在方位向进行加权处理并计算FFT。最终得到直角坐标系下的复数聚焦影像。

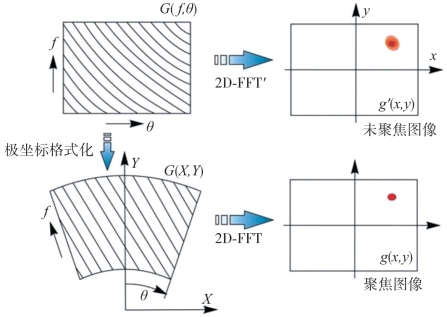
图3-5　极坐标格式化成像算法

除了影像大小受限之外，极坐标格式化算法的另一个缺陷是在傅里叶变换之前需要进行较为耗时的频域差值计算，仅适用于GBSAR远场条件下小范围场景的成像。在远场条件下，通过定义一个伪极坐标系可以避免这一差值计算过程，即远场伪极坐标格式化算法（Far-Field Pseudo-polar Format Algorithm）。假设孔径长度L的雷达远场区域内有一点P，P点到合成孔径中心（或天线阵列中心）的距离是ρ，中心线偏角为θ，P点到雷达天线位置的距离是ρ＇，中心线偏角为θ＇。

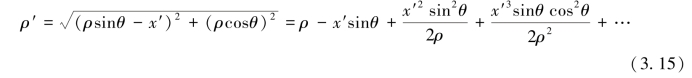
在远场条件下有ρ，ρ＇≫L，略去高阶，P点的雷达天线距近似为(www.daowen.com)

P点的雷达反射信号可以写为

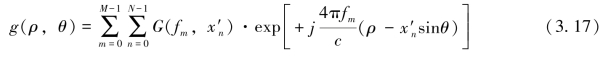
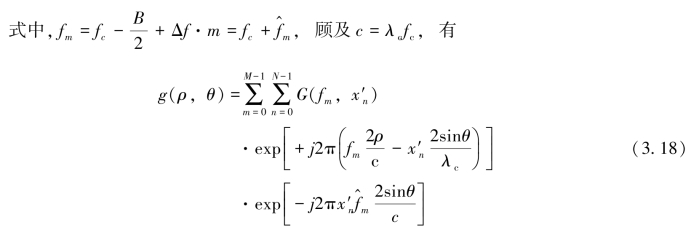
第一个指数项为傅里叶变换的核，利用它定义伪极坐标系

类似于（ρ，θ）定义的极坐标系，α与坐标系中的距离ρ成正比，β是偏角θ的正弦函数，振幅为。伪极坐标系到极坐标系的转换如式（3.20）所示：

相应地，目标在笛卡儿坐标系下的横纵坐标为

利用远场伪极坐标格式化算法获取P点的回波成像为

式中，FFT2[·]是二维快速傅里叶变换算子，结合式（3.20）和式（3.21）可以完成伪极坐标系到极坐标系或笛卡儿直角坐标系的转换，计算的时间复杂度是O（NM log2M）。

伪极坐标格式化算法适用于雷达天线远场区域的成像。和极坐标格式化算法不同，该算法在影像中各点均不会引入几何畸变。该算法在伪极坐标系下直接应用二维FFT，不需要在成像前进行任何的差值计算。远场伪极坐标格式化算法在保证成像精度的情况下是一种高效的计算方法，而且在其伪极坐标系下整幅影像具有一致的分辨率，便于数据的存储。

3.空变匹配滤波成像算法

空变匹配滤波成像算法（Space-Variant Matched-Filter Imaging Algorithm）是一种近场快速成像算法，最开始用于逆合成孔径雷达（ISAR）成像，Fortuny 1994年将该方法稍加改进用于近场SAR的快速成像，算法的核心是聚焦算子的计算。

假设天线系统以球面波的形式辐射监测目标，且辐射样式未发生畸变，那么高度h处目标的二维散射方程可以用式（3.23）描述：

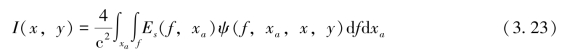
式中，c为光速，xa为目标在方位向上的位置，Es（f，xa）是探测到的后向散射信号，ψ（f，xa，x，y）是聚焦算子，如式（3.24）所示：

聚焦算子可以写为ψ（f，x-xa，y），变化后，后向散射函数与聚焦算子的计算可以看作傅里叶域的卷积，可以应用FFT进行高效的计算。该方法在频域不需要插值，减少了部分计算时间；成像精度高，适用于多种扫描几何形式；除了自由空间目标物的二维和三维成像外，这种算法也可以用于地探雷达成像。JRC的LISA系统在最初设计时便采用了该成像算法。