轴向存速模型以复合结构侵彻体整体为对象，通过分析侵彻过程中受力状态，研究侵彻体轴向剩余速度和弹道极限。根据矢量法则，破片实际速度由其轴向和径向速度矢量合成。忽略壳体在破碎过程中的能量消耗，可认为破片具有与剩余侵彻体相同的轴向剩余速度vres，则破片实际最大飞散速度表述为

基于Ranking-Hugoniot（RH）关系，质量、动量及能量守恒可表述为

式中，ρ为密度；U为冲击波速；u为粒子速度；p为压力；e为比内能。下标0和1分别代表未冲击区域状态和已冲击区域状态。当材料处于一维应变状态时，上述关系成立。相比于壳体和破片材料，该近似关系更适用于描述芯体材料。粒子速度和冲击波速线性关系可表述为

式中，c0和s分别为与材料有关的常数。与式（2.20）联立，可得材料压力与粒子速度间关系

芯体材料中压力载荷确定时，芯体和壳体间径向压力即可计算获得。径向压力与壳体的碎裂有关，其产生的前提条件是，壳体的径向膨胀小于芯体径向膨胀。芯体径向膨胀可通过胡克定律计算，应变与轴向应力（σr）和径向应力（σx）有关，可表述为

其中，εf为应变；r为半径；v为材料泊松比，E为杨氏模量。当壳体不再产生新的径向膨胀时，径向膨胀表述为(www.daowen.com)

作用于壳体的径向压力同样在相反方向作用于芯体，因此有σr，j=-σr，j。由于芯体与靶板作用面上应力、半径相等，径向压力可表述为

壳体径向加速度可通过牛顿运动定律表述为

式中，mj为壳体质量；σθ为环向应力；Ai和Ac分别为壳体内表面面积和壳体横截面面积。壳体开始发生碎裂时，径向作用力（Aiσr）大于环向作用力（Acσθ），并达到材料的强度极限，直到壳体应变达到其碎裂应变，随后环向应力变为0。壳体破片被径向加速直到芯体材料达到其最大膨胀：

除壳体径向速度，还可通过Mott金属壳体膨胀理论获得壳体碎片质量分布，碎片平均质量可表述为

式中，σfr为碎裂应力；γ为Mott常数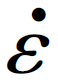；fr为壳体在碎裂时径向膨胀应变率。壳体几何系数定义为α=l/b·t/b，l、b、t分别为壳体碎片长度、宽度、厚度。