侵彻毁伤模式与侵彻体材料特性、结构形状、碰撞条件、靶板材料、厚度以及结构等都有直接联系。按厚度，靶板类型可分为以下几种。

（1）薄靶：侵彻体侵彻过程中沿靶板厚度方向应力应变无梯度分布。

（2）中厚靶：侵彻体侵彻过程中会受到远方边界表面影响。

（3）厚靶：侵彻体进入靶板相当距离后才受到远方边界表面影响。

（4）半无限靶：侵彻体侵彻过程中不受远方边界表面影响。

侵彻作用下，不同厚度靶板破坏模式不同，主要包括脆性破坏、层裂破坏、冲塞破坏、花瓣形穿孔、崩落破坏、延性穿孔等类型。

脆性破坏一般出现于靶板材料拉伸强度明显低于压缩强度时。侵彻过程中，弹丸撞击产生的压缩应力超过靶板材料抗压强度，穿孔处将产生大量向外延伸的径向裂纹，典型脆性破坏毁伤模式如图1.12（a）所示。

靶板材料压缩强度大于拉伸强度时，弹丸侵彻作用下，在非加载表面附近，一个或多个稀疏波相互作用导致靶板材料发生失效，形成层裂；对低密度靶板，初始应力超过材料极限强度时也易导致材料发生层裂，如图1.12（b）所示。

柱形或钝头弹侵彻刚性薄靶或中厚靶时，弹丸挤压作用下，弹靶接触位置环形截面处产生显著剪切效应，并同时产生热量。由于侵彻过程速度较高，产生的热量无法及时传导，剪应力聚集区域温升显著，靶板局部抗剪强度降低，随弹丸侵彻产生柱状塞块，即为冲塞破坏，如图1.12（c）所示。

图1.12　典型靶板破坏模式

外形变化很大的弹丸侵彻延性薄靶时，首先引起沿穿孔的星形径向破坏。弹丸继续侵彻时，星形裂纹向整个靶板厚度和径向扩展，裂纹间角料转折成花瓣状，在靶板上形成花瓣形穿孔，如图1.12（d）所示。

钝头弹侵彻强度较低中厚靶时，由于弹丸撞击，靶板受到强烈冲击，靶内产生压缩应力波。压缩应力波传到靶板背面发生发射，形成一道自靶板背面与反射应力波传播方向相反的拉伸波。入射压缩波与反射拉伸波相互干涉，在靶内一定厚度处出现拉伸应力并超过靶板抗拉强度，靶板背面产生崩落碎片，导致靶板产生崩落破坏，如图1.12（e）所示。

锥形或卵形头部弹丸侵彻延性靶时，由于弹丸挤压，靶板穿孔处产生剧烈膨胀，靶板材料轴向和径向塑性变形，被挤向穿孔入口和出口处，并随弹丸贯穿过程将孔口扩大，在靶板上形成延性穿孔，如图1.12（f）所示。

对于锥头弹丸正撞击下延性金属靶板的破坏，延性穿孔和冲塞破坏是两种最主要的破坏模式。从本质上讲，不同耗能机制和运动破坏过程决定最终破坏模式：随侵入深度的增加，弹丸不断将靶体材料挤向两侧，当弹丸头部到达靶板背面时，靶板发生延性扩孔；弹丸头部压入靶体过程中，由于弹靶相互作用，在接触区边缘形成剪切合力，达到材料剪切破坏极限后，则形成冲塞破坏。

若仅考虑靶板的局部变形，则以上两种破坏模式的转化临界条件为：当弹丸头部刚达到靶板背面的同时满足了剪切破坏条件。根据H与Ln的大小，该转换模式的出现面临两种情况，如图1.13所示。

图1.13　不同临界条件下弹靶作用模型

当H＞Ln时，典型弹靶作用模型如图1.13（a）所示，弹丸尖部刚好达到靶板背面且满足剪切破坏条件。假设不考虑速度效应影响和塑性变形堆积，靶体材料对弹丸表面的压力可表述为σn=ασy，式中系数α可表述为

由靶体材料对弹丸表面压力方程

临界锥角θc可表述为

当H＜Ln时，典型弹靶作用模型如图1.13（b）所示。弹丸尖部刚好达到靶板背面且满足剪切破坏条件，此时弹丸的圆柱段尚未侵入靶体，仍假定弹丸表面压力为σn=σ0，靶体材料对弹丸表面压力方程可表述为

比较式（1.4）和式（1.3）可以发现，两种条件下锥角θ表达式相同。根据式（1.1）和式（1.4），可获得临界锥角θc与几何参数H/d、靶板的材料参数σy、E、Ep等因素关系，表明靶板材料屈服应力越大，弹头临界锥角越大。

为便于分析，引入变量K2，定义为：当Fmax=Fc时，H/d=K2。根据靶板厚度（H）与锥头部分长度（Ln）之间的相对大小和厚径比H/d与K1之间的相对大小，K2的值有如下四种情况：

（1）当H≤Ln，H/d＜K1时，K2通过式（1.5）计算：(www.daowen.com)

（2）当H≤Ln，H/d≥K1时，K2可表述为

（3）当H＞Ln，H/d＜K1时，K2通过式（1.7）计算：

（4）当H＞Ln，H/d≥K1时，K2可表述为

需要特别指出的是，薄靶的破坏行为往往表现为伴有整体变形的简单剪切破坏，无绝热剪切现象的出现。基于Wen-Jones模型，忽略绝热剪切效应，可分析包含整体大变形的平头弹丸冲击下靶板冲塞破坏。

从机理上讲，材料绝热剪切破坏是热软化和塑性应变硬化竞争的结果，当绝热温升导致的热软化超过塑性应变硬化时，材料的承载能力开始降低，随即发生绝热剪切破坏。首先分析简单剪切破坏与绝热剪切冲塞破坏的临界条件，对于有总体变形的情况，该模型基于剪切塑性铰的理论给出了靶板发生局部剪切破坏时，弹丸的局部侵入深度Pc，可表述为

根据绝热剪切模型，绝热剪切失稳时弹丸的局部侵入深度Pi可表述为

比较Pi和Pc值，靶板将出现两种破坏模式：Pi＜Pc时，靶板破坏时发生绝热剪切失稳；Pi＞Pc时，靶板局部剪切破坏时无绝热剪切失稳。

该过程中两种破坏模式转化的临界条件即为Pi=Pc，则根据式（1.9）和式（1.10），结合绝热剪切失稳临界剪应变γi，两种破坏模式转化时临界厚径比（H/d）c为

式（1.11）表明，材料的硬化较强，τ0和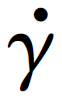m较小时，发生绝热剪切失稳的临界厚径比更大。同时，通过以上分析可知，当H/d＜K2时，靶板为薄靶；当H/d≥K2时，靶板为厚靶。

对于厚靶的冲塞破坏，存在两种破坏模式，一是弹头压入后发生绝热冲塞破坏，通过两阶段冲塞模型分析；二是作用过程由弹头压入阶段、侵彻扩孔阶段和绝热冲塞阶段组成，通过三阶段冲塞模型分析。研究表明，当金属靶板在锥头弹丸正侵彻下产生冲塞破坏时，若H/d≤（H/d）c2，即可通过二阶段冲塞破坏模型分析；若H/d＞（H/d）c2，即可通过三阶段冲塞破坏模型分析。

临界厚径比（H/d）c2表述为

式中，τM为材料发生绝热剪切失稳时对应的最大剪切应力。

基于上述分析，临界锥角θ随H/d变化如图1.14所示。结合式（1.11），冲塞破坏时，若H/d≤（H/d）c，则为简单剪切破坏；若H/d＞（H/d）c，为绝热剪切破坏；若H/d＞（H/d）c2，则破坏过程前期为扩孔过程，后期为绝热冲塞破坏。

图1.14　临界锥角θ随H/d变化

综上所述，图1.14可分为若干破坏区域，分别为以下几方面。

（1）当θ＜θc且H/d＜K2时，为薄靶的扩孔破坏。

（2）当θ＜θc且H/d≥K2时，为厚靶的扩孔破坏。

（3）θ≥θc且H/d＜K2时，为简单剪切冲塞破坏。

（4）θ≥θc且K2≤H/d≤（H/d）c2时，为绝热剪切冲塞破坏。

（5）当H/d＞（H/d）c2时，为先扩孔后绝热冲塞破坏。

由图1.14中可知，随着H/d增大，弹丸临界锥角θc先减小，当H/d达到一定值时，弹丸的临界锥角θc逐渐趋于一定值。考虑到θc的物理意义，可以认为当θc≥0时，靶板发生冲塞破坏，即为图1.14中θc曲线上方的区域；当θ＜θc时，靶板发生扩孔破坏，即为图1.14中θc曲线下方的区域。

对扩孔破坏模式而言，K2值根据方程（1.5）～方程（1.8）求解。由图1.14可知，对于扩孔破坏，K2与弹丸锥角θ相关，θ值较大时K2值也较大。同时，θ取值还与靶板固支半径与弹丸半径比值R/a有关。