1）实验要求

（1）建立一阶RC电路，观察一阶RC电路的零输入响应、零状态响应和全响应的变化规律和特点。

（2）掌握一阶RC电路近似构成微分电路或积分电路的条件，并观察微分电路、积分电路的输入、输出波形。

（3）建立二阶RLC串联电路，观测二阶电路在不同类型下的状态轨迹，分析电路参数对响应波形的影响。

2）电路基本原理

通常称包含L、C的电路为动态电路。描述动态电路的方程用微分方程，电路的阶数决定微分方程的阶数。

（1）一阶RC电路

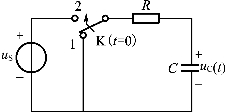
图5.51　一阶RC电路

含有一个储能元件和电阻的电路称为一阶电路，有RC、RL两种电路。下面以一阶RC电路为例进行分析。

①图5.51中，首先将开关K置于1位置，使电路处于零状态，在t=0时刻由1扳向2，电路对激励uS的响应为零状态响应：uC（t）=US（1-e-t/RC），这一暂态过程为电容充电的过程；若开关K首先置于2位置使电路处于稳定状态，在t=0时刻由2扳向1，电路为零输入响应：uC（t）=USe-t/RC，这一暂态过程为电容放电的过程。

动态电路的零状态响应和零输入响应之和称为全响应。

②RC电路充、放电的时间常数τ可以从示波器观察的响应波形计算得出。设时间坐标单位确定，对于充电曲线，幅值由零上升到终值的63.2%所需的时间为时间常数τ。对于放电曲线，幅值下降到初值的36.8%所需的时间同为时间常数τ。

③一阶RC动态电路在方波激励下，可以近似构成微分电路或积分电路。当时间常数τ（τ=RC）远远小于激励方波周期T时，如图5.52（a）所示为微分电路，输出电压uo（t）与方波激励uS的微分近似成比例。当时间常数τ（τ=RC）远远大于激励方波周期T时，如图5.52（b）所示为积分电路，输出电压uo（t）与方波激励uS的积分近似成比例。

图5.52　微分电路、积分电路

（2）RLC二阶电路

用二阶微分方程描述的动态电路称为二阶电路，二阶电路的组合形式较多，以RLC串联电路为例进行分析，如图5.53所示。研究二阶电路在方波激励时，电路的响应动态过程。

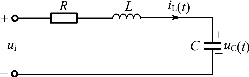
图5.53　RLC二阶电路

RLC串联电路构成的二阶电路，无论是零状态响应，还是零输入响应，电路瞬态过程的性质，完全由特征方程的特征根来决定。

①当时，称为过阻尼，响应为非振荡型。

②当时，称为临界阻尼，响应处于振荡与非振荡之间，响应为临界振荡型。

③当时，称为欠阻尼，响应将出现减幅振荡，为振荡型。

④当R=0时，电路动态过程性质为等幅振荡，即无阻尼情况。

⑤当R＜0，电路动态过程性质为发散振荡，即负阻尼情况。

在一般电路中，总存在一定的电阻，只有接入特殊器件（负电阻），方可实现无阻尼和负阻尼情况。(www.daowen.com)

3）Multisim 12仿真分析

（1）建立如图5.54（a）所示的一阶RC测试电路。设定延时开关参数：Time On为0.2 ms，Time Off为0.6 ms。

①打开仿真开关，通过示波器观察到电容两端电压的波形如图5.54（b）所示。

由理论计算得：当t=τ时，UC=5×0.632=3.16（V），从图5.54（b）中的曲线找到其对应的时间为106 μs，所以τ=0.106 ms。理论计算值τ=RC=0.1 ms。

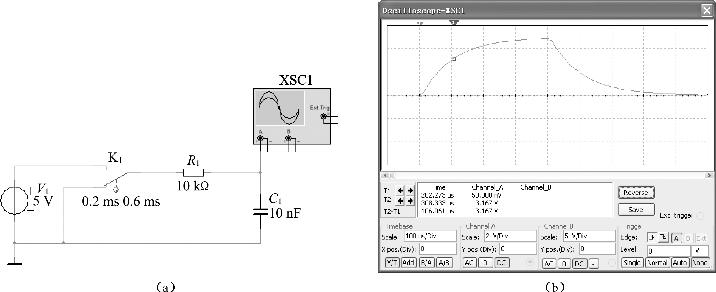
图5.54　一阶RC电路及电容两端电压波形

②建立如图5.55（a）所示电路，函数信号发生器输出设置为方波，频率为100 Hz，幅值为5 V。因τ=0.01T，远远小于激励方波周期T，所以此时一阶RC电路构成微分电路。

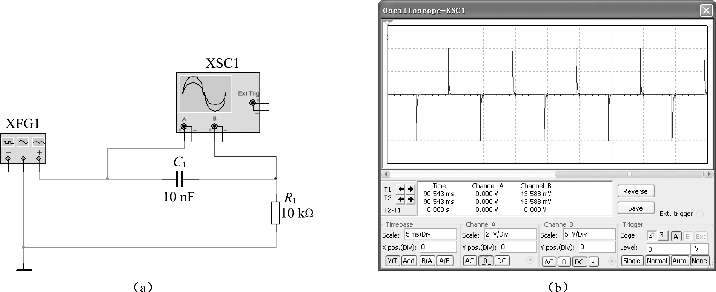
图5.55　微分电路及输出电压波形

打开仿真开关，通过示波器观察电路的输出电压波形如图5.55（b）所示。从图5.55（b）可看出，利用微分电路可以实现从方波到尖脉冲波形的转变。

③建立如图5.56（a）所示电路，函数信号发生器输出设置为方波，频率为50 kHz，幅值为5 V。因τ=5T，所以此时一阶RC电路构成积分电路。

打开仿真开关，通过示波器观察电路的输入、输出电压波形如图5.56（b）所示。从图5.56（b）可看出，利用积分电路可以实现从方波到三角波的转变。

（2）建立如图5.57所示的RLC二阶电路。因为示波器只能显示电压波形，为观测iL（t）的响应波形，需要将电流分量转换成电压分量，为此在电路中串联一个很小的电阻R0（电流取样电阻），示波器接到电阻端，此时显示的即是iL的波形。

①观察二阶电路的响应波形uC（t）、iL（t）

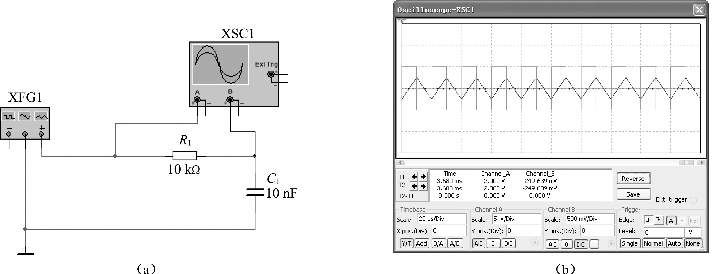
图5.56　积分电路及输入、输出电压波形

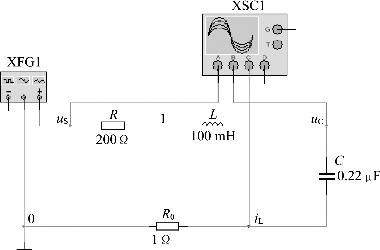
图5.57　RLC二阶电路

设置函数信号发生器的输出频率为125 Hz、占空比为50%、幅值为4 V的方波信号。电路的输入波形uS（t）和响应波形uC（t）、iL（t）如图5.58所示。

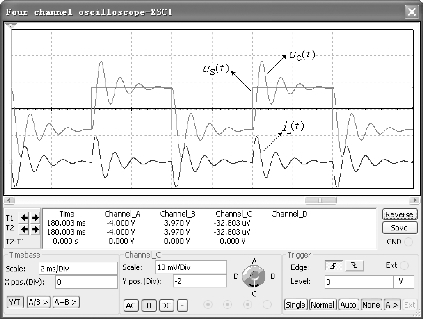
图5.58　uS（t）、uC（t）、iL（t）波形

②分析电阻R对电路响应波形的影响

在菜单栏中依次执行Simulate/Analyses/Parameter Sweep（参数扫描）命令，设置扫描方式为List（取列表值扫描），设置R扫描时的不同电阻值为0、200 Ω、1.2 kΩ、3 kΩ，设置分析种类为Transient Analysis（瞬态分析），终止分析时间设置为8 ms，时间步长设为1 000，设置输出节点为uS、uC，可得到不同阻值时二阶电路的响应波形uC（t），如图5.59所示。

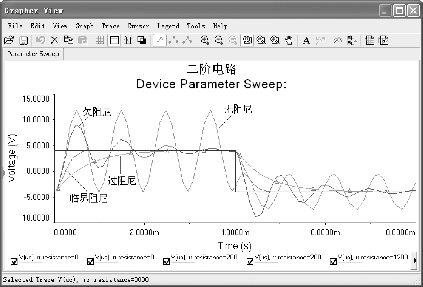
图5.59　不同阻值时二阶电路的响应波形uC（t）

从图5.59的分析结果可以看出，在如图5.57所示二阶电路中，当R=0时为无阻尼状态，响应将出现等幅振荡；当R=200 Ω时为欠阻尼状态，响应为振幅按指数衰减的正弦振荡；当R=1.2 kΩ时为临界阻尼状态；当R=3 kΩ时为过阻尼状态。二阶电路各种状态的响应曲线如图5.59所示。