1）实验目的

（1）掌握半加器、全加器及数据选择器、分配器的工作原理。

（2）熟悉常用全加器、半加器及数据选择器、分配器的管脚排列和逻辑功能。

（3）学习用数据选择器设计组合逻辑电路的方法。

2）实验原理

（1）半加器和全加器

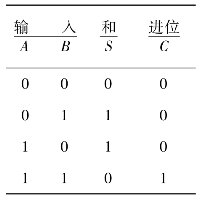
如果不考虑有来自低位的进位将两个1位二进制数相加，称为半加。实现半加运算的电路叫做半加器。根据组合电路设计方法，首先按照二进制加法运算规则可列出半加器的真值表，见表4.16。

表4.16　半加器真值表

写出半加器的逻辑表达式：

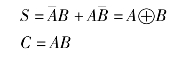
若用与非门来实验，即为

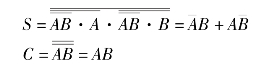
半加器的逻辑电路图如图4.40所示。

在实验过程中，我们可以选异或门74LS86及与门74LS08实现半加器的逻辑功能，也可用与非门74LS00和反相器74LS04组成半加器。

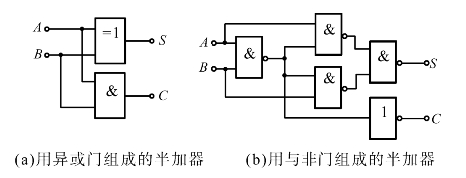
图4.40　半加器逻辑电路图

在将两个多位二进制数相加时，除了最低位以外，每一位都应该考虑来自低位的进位，即将两个对应位的加数和来自低位的进位3个数相加。这种运算称为全加，所用的电路称为全加器。

用两个半加器可组成全加器，原理如图4.41所示。选用的集成双全加器74LS183其管脚排列如图4.42所示。

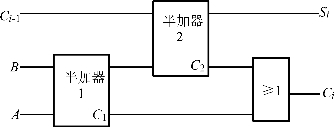
图4.41　由两个半加器组成的全加器

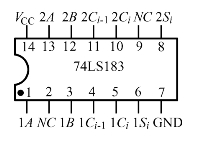
图4.42　74LS183双全加器管脚图

（2）数据选择器和数据分配器

数据选择器又叫多路开关，其基本功能相当于单刀多位开关，其集成电路有“四选一”“八选一”“十六选一”等多种类型。这里我们以“八选一”数据选择器74LS151为例进行实验论证。

数据选择器的应用很广，它可以实现任何形式的逻辑函数，将并行码变成串行码，组成数码比较器等。例如，在计算机数字控制装置和数字通信系统中，往往要求将并行形式的数据转换成串行的形式。若用数据选择器就能很容易地完成这种转换。只要将要变换的并行码送到数据选择器的信号输入端，使组件的控制信号按一定的编码（如二进制码）顺序依次变化，则在输出端可获得串行码输出，如图4.43所示。

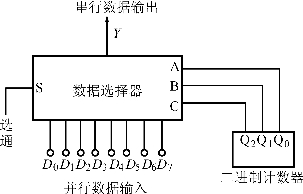
图4.43　变并行码为串行码

实际上，数据分配器的逻辑功能与数据选择器相反。它的功能是使数据由1个输入端向多个输出端中的某个输出端进行传送，它的电路结构类似于译码器，所不同的是多了一个输入端。若选择器输入端恒为1，它就成了上一实验的译码器。实际上，我们可以用译码器集成产品充当数据分配器。例如，用2-4线译码器充当4路数据分配器，3-8线译码器充当8路数据分配器。就是将译码器的译码输出充当数据分配器的输出，而将译码器的使能输入充当数据分配器的数据输入。

数据选择器和分配器组合起来，可实现多路分配，即在一条信号线上传送多路信号。这种分时传送多路数字信息的方法在数字技术中经常被采用。

（3）数据选择器的应用——实现组合逻辑函数

数据选择器是地址选择变量的最小项输出器，而任何一个逻辑函数都可以表示为最小项之和的标准形式。因此，用数据选择器可以很方便地实现逻辑函数，如采用八选一数据选择器74LS151可实现任意三输入变量的组合逻辑函数。

例：用八选一数据选择器74LS151实现函数F=AB+AC+BC。

①表达式比较法

a.写出逻辑函数的最小项表达式

b.写出数据选择器的输出函数表达式

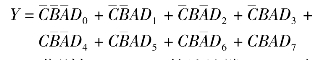
c.将函数F中的C、B、A分别与74LS151的地址端C、B、A相对应，比较F和Y两式中最小项的对应关系，则为了使F=Y，应令：

D0=D1=D2=D4=0

D3=D5=D6=D7=1

d.画出实现函数F的接线图，如图4.44所示。

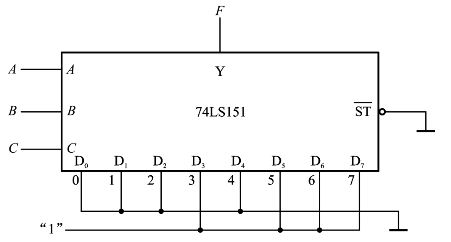
图4.44　74LS151实现函数F=AB+AC+BC

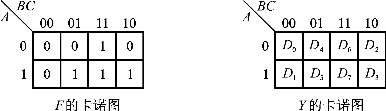
图4.45　逻辑函数与数据选择器的卡诺图(www.daowen.com)

②卡诺图比较法

a.画出逻辑函数F与数据选择器输出Y的卡诺图，如图4.45所示。

b.将函数F中的C、B、A分别与74LS151的地址端C、B、A相对应，比较逻辑函数F与数据选择器输出Y的卡诺图，则为了使F=Y，应令：

D0=D1=D2=D4=0

D3=D5=D6=D7=1

c.画出接线图：与表达式比较法结果相同。

由上述例子可看出，当逻辑函数的变量数m和数据选择器的地址数n相同时，可直接用数据选择器来实现逻辑函数。

当逻辑函数的变量数m大于地址数n时，应从m个变量中选择n个直接作为数据选择器的地址输入，然后求出其余（m-n）个输入变量所组成的子函数，并将它们加到数据选择器相应的数据输入端。

当逻辑函数的变量数m小于地址数n时，应将不用的地址端及不用的数据输入端都接地。

3）实验内容

（1）半加器和全加器

①将二输入四异或门74LS86和二输入四与门74LS08按电路图4.40（a）接线，进行实验论证；将二输入四与非门74LS00和非门74LS04按电路图4.40（b）接线进行实验论证。

将A、B分别接实验系统逻辑开关K1、K2，输出S和C接发光二极管LED。按半加器真值表输入K1、K2逻辑电平信号，观察输出结果和S及进位C，验证表4.16。

②验证全加器74LS183的功能

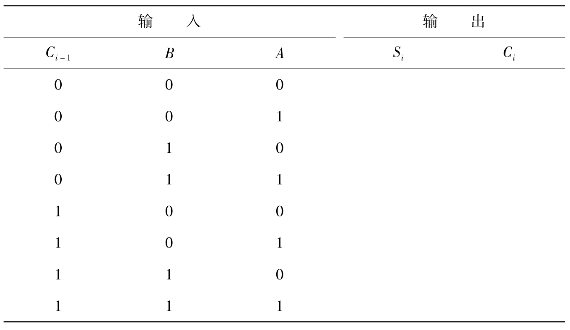
将A、B、Ci-1分别接实验系统逻辑开关K1、K2、K3，输出Si和Ci接发光二极管LED，观察输出结果和Si及进位Ci，完成表4.17。

表4.17　全加器逻辑功能

（2）数据选择器和分配器

①将实验用74LS151八选一数据选择器插入实验系统中。74LS151管脚如图4.46所示，按图4.47接线。

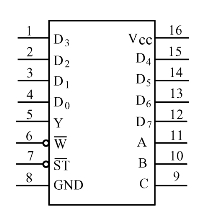
图4.46　74LS151管脚图

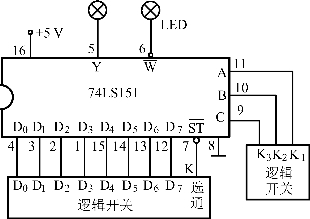
图4.47　八选一数据选择器实验接线图

其中C、B、A为三位地址码，为低电平选通输入端，D0～D7为数据输入端，输出Y为原码输出端，为反码输出端。

置选通端为“0”电平，数据选择器被选中，拨动逻辑开关K3～K1分别为000，001，…，111（置数据输入端D0～D7分别为10101010或11110000），观察输出端Y和输出结果并记录（表格自拟）。实验结果表明，图4.47实现了并行码变串行码的转换。

②译码器常常可接成数据分配器，在多路分配器中即用3-8线74LS138译码器接成数据分配器形式，从而完成多路信号的传输，具体实验接线如图4.48所示。

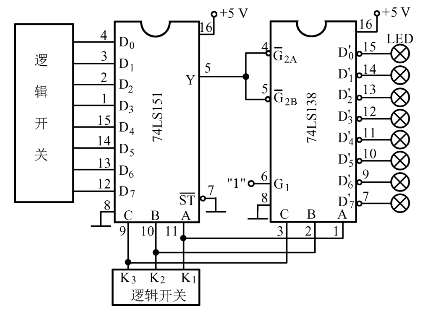
图4.48　多路信号的传输（多路分配器）

按图4.48接线，D0～D7分别接数据开关或逻辑开关，D0′～D7′接8个发光二极管LED显示，数据选择器和数据分配器地址码一一对应相连，并接3位逻辑电平开关（也可用8421码拨码开关的4、2、1三位或3位二进制计数器的输出端QC、QB、QA）。把数据选择器74LS151原码输出端Y与74LS138的输入端相连，两个芯片的选通分别接规定的电平。这样即完成了多路分配器的功能。

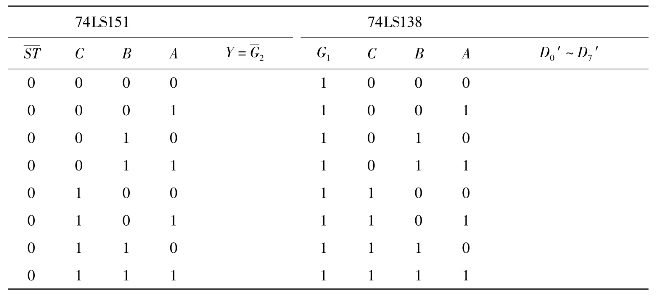
置D0～D7为11110000和10101010两种状态，再分别两次置地址码C、B、A为000～111，观察输出发光二极管LED状态，完成表4.18。

表4.18　多路分配器实验结果（D0～D7为11110000）

（3）数据选择器的应用——实现组合逻辑函数

用八选一数据选择器74LS151实现逻辑函数F=A¯B+¯AB+¯AC，写出设计过程，画出接线图，并验证电路逻辑功能。

4）预习要求

（1）复习半加器、全加器、数据选择器、数据分配器的工作原理和特点。

（2）了解本实验中所用集成电路的逻辑功能和使用方法。

5）实验报告

（1）整理实验数据和实验线路图。

（2）试用数据选择器实现全加器及比较器的功能，画出具体线路图。

6）实验设备

（1）数字电路实验系统（SDS-Ⅵ）一台

（2）集成电路：74LS00、74LS04、74LS08、74LS86、74LS183、74LS138、74LS151各一片

7）思考题

（1）能否用八选一数据选择器74LS151实现四变量的逻辑函数？

（2）用八选一数据选择器74LS151设计本章实验4中的第2个课题（血型匹配判断电路）。