1）实验目的

（1）了解电信号的采样方法与过程以及信号恢复的方法。

（2）验证抽样定理。

2）实验设备

（1）TKSS-C型信号与系统实验箱　　　　一台

（2）YB4340G型双踪示波器一台

3）实验原理

图2.54　矩形抽样脉冲

（1）离散时间信号可以从离散信号源获得，也可以从连续时间信号抽样而得。抽样信号fS（t）可以看成连续信号f（t）和一组开关函数S（t）的乘积。S（t）是一组周期性窄脉冲，见图2.54，TS称为抽样周期，其倒数fS=1/TS称为抽样频率。

对抽样信号进行傅里叶分析可知，抽样信号的频率包括了原连续信号以及无限个经过平移的原信号频率。平移的频率等于抽样频率fS及其谐波频率2fS、3fS…。当抽样信号是周期性窄脉冲时，平移后的频率幅度按（sinx）/x规律衰减。抽样信号的频谱是原信号频谱周期的延拓，它占有的频带要比原信号频谱宽得多。

（2）正如测得了足够的实验数据以后我们可以在坐标纸上把一系列数据点连起来，得到一条光滑的曲线一样，抽样信号在一定条件下也可以恢复到原信号。只要用一截止频率等于原信号频谱中最高频率fn的低通滤波器，滤除高频分量，经滤波后得到的信号包含了原信号频谱的全部内容，故在低通滤波器输出端可以得到恢复后的原信号。

（3）原信号得以恢复的条件是fS≥2 BW，其中fS为抽样频率，BW为原信号占有的频带宽度。而fmin=2 BW为最低抽样频率，又称“奈奎斯特抽样频率”。当fS＜2 BW时，抽样信号的频谱会发生混叠，从发生混叠后的频谱中我们无法用低通滤波器获得原信号频谱的全部内容，在实际使用中，仅包含有限频率的信号是极少的，因此即使fS=2 BW，恢复后的信号失真还是难免的。

图2.55画出了当抽样频率fS＞2 BW（不混叠时）及fS＜2 BW（混叠时）两种情况下冲激抽样信号的频谱。

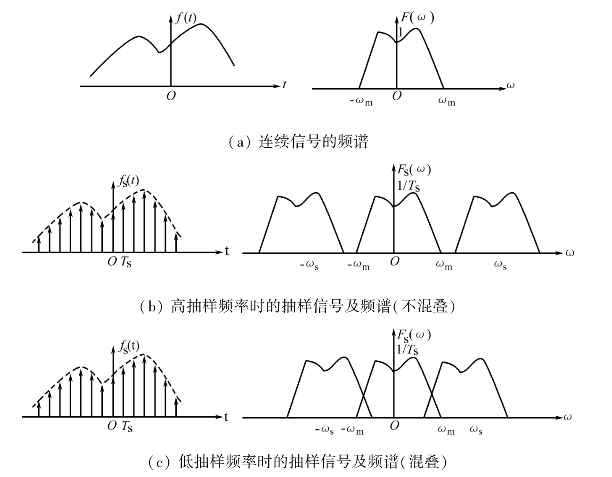
图2.55　冲激抽样信号的频谱(www.daowen.com)

（4）为了实现对连续信号的抽样和抽样信号的复原，可用实验原理框图2.56的方案。

图2.56　抽样定理实验原理方框图

除选用足够高的抽样频率外，常采用前置低通滤波器来防止原信号频谱过宽而造成抽样后信号频谱的混叠，但这也会造成失真。如实验选用的信号频带较窄，则可不设前置低通滤波器。本实验就是如此。

4）预习要求

（1）若连续时间信号为50 Hz的正弦波，开关函数为TS=0.5 ms的窄脉冲，试求抽样后信号fS（t）。

（2）设计一个二阶RC低通滤波器，截止频率为5 kHz（选做）。

5）实验内容

（1）将频率为100 Hz左右的正弦波f（t）和采样脉冲信号S（t）送入抽样器，观察正弦波经抽样后的信号。

（2）改变抽样频率为fS≥2 BW和fS＜2 BW，观察复原后的信号，比较其失真程度。

6）实验报告

（1）整理并绘出原信号、抽样信号以及复原信号的波形，你能得出什么结论？

（2）若原信号为方波或三角波，可用示波器观察到离散的抽样信号，但由于本装置难以实现一个理想的低通滤波器，以及高频窄脉冲（即冲激函数），所以方波或三角波的离散信号经低通滤波器后只能观测到它的基波分量，无法恢复原信号。

7）思考题

（1）观察经低通滤波器恢复后无失真的信号与原输入信号之间的幅度关系，计算放大倍数和延时。

（2）若连续时间信号取频率为200～300 Hz的正弦波，计算其有效的频带宽度。该信号经频率为fS的周期脉冲抽样后，若希望通过低通滤波后的信号失真较小，则抽样频率和低通滤波器的截止频率应取多大？试设计一个满足上述要求的低通滤波器。