1）实验目的

（1）了解二阶网络函数的电路模型。

（2）研究系统参数变化对响应的影响。

（3）用基本运算放大器模拟系统的微分方程和传递函数。

2）实验设备

（1）TKSS-C型信号与系统实验箱一台

（2）YB4340G型双踪示波器一台

3）实验原理

（1）微分方程的一般形式为：

yn+an-1yn-1+…+a0y=x

式中：x为激励，y为响应。模拟系统微分方程的规则是将微分方程输出函数的最高阶导数保留在等式左边，把其余各项一起移到等式右边，这个最高阶导数作为第一积分器输入，以后每经过一个积分器，输出函数导数就降低一阶，直到输出y为止。各个阶数降低了的导数及输出函数分别通过各自的比例运算器再送至第一个积分器前面的求和器，与输入函数x相加，则该模拟装置的输入和输出所表征的方程与被模拟的实际微分方程完全相同。

图2.49、图2.50分别为一阶微分方程的模拟框图和二阶微分方程的模拟框图。

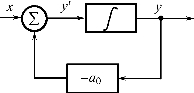
图2.49　一阶系统的模拟框图

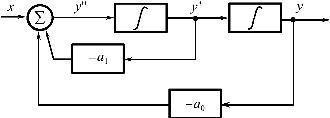
图2.50　二阶系统的模拟框图

（2）网络函数的一般形式为：

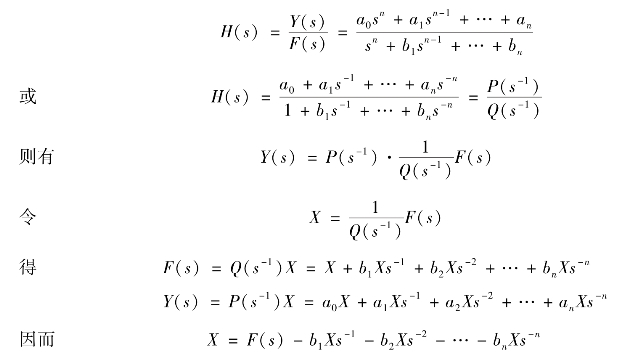
根据上式，可画出如图2.51所示的模拟方框图，图中s-1表示积分器。

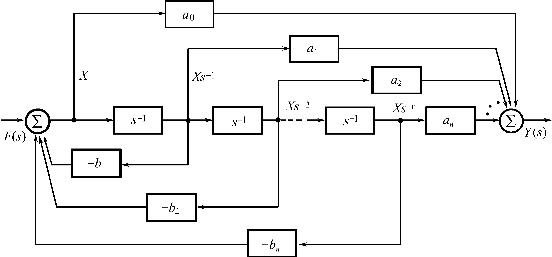
图2.51　网络函数的模拟框图

图2.52为二阶网络函数的模拟方框图，由该图求得下列3种传递函数，即

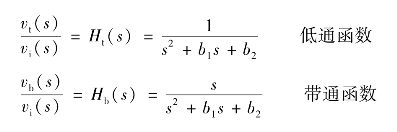
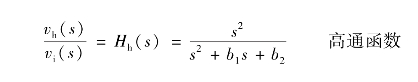(www.daowen.com)

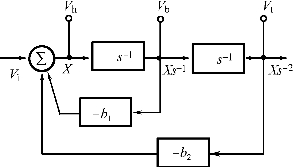
图2.52　二阶网络函数的模拟框图

图2.53为图2.52的模拟电路图。

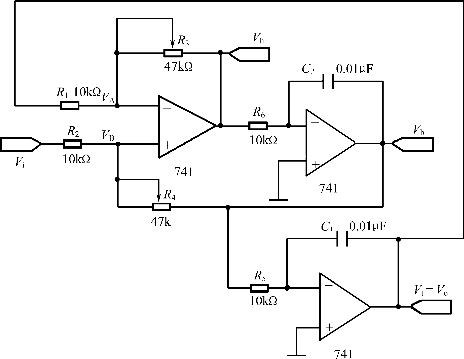
图2.53　二阶网络函数的模拟电路图

由该模拟电路得：

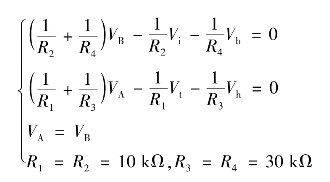
由上述方程组并结合图2.53中各元件参数可推出：

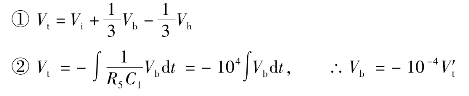
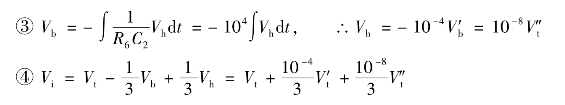
只要适当地选择模拟装置相关元件的参数，就能使模拟方程和实际系统的微分方程完全相同。

4）实验内容

（1）在TKSS-C型信号与系统实验箱中的自由布线区设计图2.53的电路图。

（2）写出实验电路的微分方程，并求解。

（3）将正弦波信号接入电路的输入端，调节R3、R4、Vi，用示波器观察各测试点的波形，并记录。

（4）将方波信号接入电路的输入端，调节R3、R4、Vi，用示波器观察各测试点的波形，并记录。

5）实验报告

（1）画出实验中观察到的各种波形。通过对经过基本运算器前后波形的对比，分析参数变化对运算器输出波形的影响。

（2）绘制二阶高通、带通、低通网络函数的模拟电路的频率特性曲线。

（3）归纳和总结用基本运算单元求解二阶网络函数的模拟方程的要点。

6）思考题

（1）微分方程的模拟解与数值解各有什么特点？

（2）试举例说明高通、带通和低通滤波器的实际应用。