1）实验目的

（1）了解RC无源和有源滤波器的种类、基本结构及其特性。

（2）分析和对比无源和有源滤波器的滤波特性。

2）实验设备

（1）TKSS-C型信号与系统实验箱一台

（2）YB4340G型双踪示波器一台

3）实验原理

（1）滤波器是对输入信号的频率具有选择性的一个二端网络，它允许某些频率（通常是某个频带范围）的信号通过，而其他频率的信号受到衰减或抑制，这些网络可以是由RLC元件或RC元件构成的无源滤波器，也可以是由RC元件和有源器件构成的有源滤波器。

（2）根据幅频特性所表示的通过或阻止信号频率范围的不同，滤波器可分为低通滤波器（LPF）、高通滤波器（HPF）、带通滤波器（BPF）和带阻滤波器（BEF）4种，它们的幅频响应曲线如图2.43所示。把能够通过的信号频率范围定义为通带，把阻止通过或衰减的信号频率范围定义为阻带。而通带与阻带的分界点的频率ωC称为截止频率或转折频率。图2.43中的|H（jω）|为通带的电压放大倍数，ω0为中心频率，ωCL和ωCH分别为低端（下限）和高端（上限）截止频率。

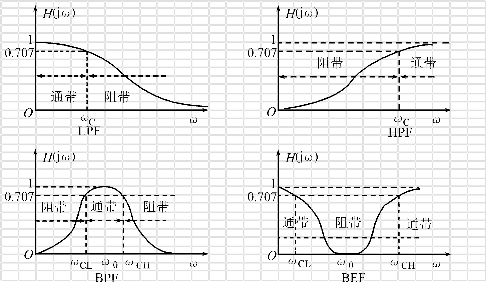
图2.43　四种滤波器的幅频响应曲线图

（3）低通滤波器的实验电路图如图2.44，高通滤波器的实验电路图如图2.45，带通滤波器的实验电路图如图2.46，带阻滤波器的实验电路图如图2.47。

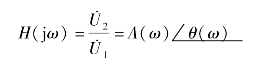
（4）如图2.48所示，滤波器的频率特性H（jω）（又称为传递函数）可用下式表示：式中：A（ω）——滤波器的幅频特性；θ（ω）——滤波器的相频特性。它们都可以通过实验的方法来测量。

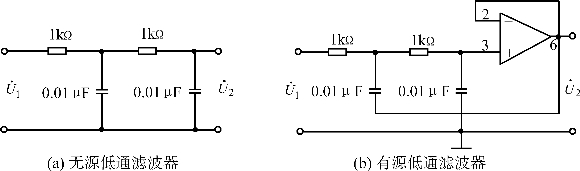
图2.44　低通滤波器

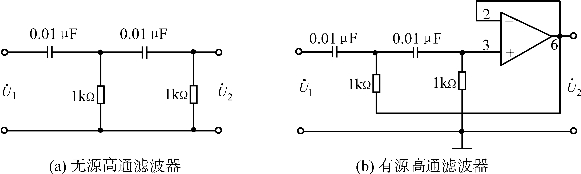
图2.45　高通滤波器

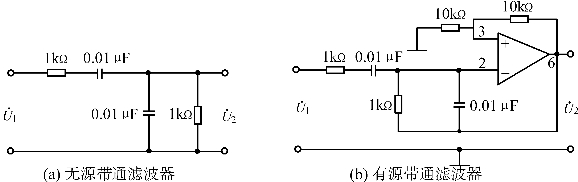
图2.46　带通滤波器

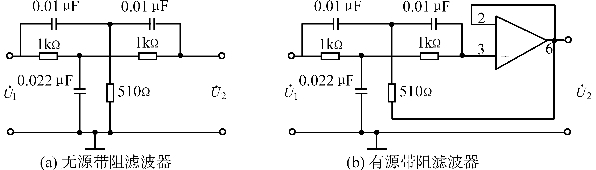
图2.47　带阻滤波器

图2.48　滤波器

4）预习要求

（1）为使实验能顺利进行，课前对教材的相关内容和实验原理、目的、要求、步骤和方法要预习。

（2）推导各类无源和有源滤波器的频率特性，并据此分别画出无源和有源滤波器的幅频特性曲线。

（3）在方波激励下，预测各类滤波器的响应情况。(www.daowen.com)

5）实验内容

（1）滤波器的输入端接正弦函数信号发生器或扫频电源，滤波器的输出端接示波器或交流数字毫伏表。

（2）测试无源和有源低通滤波器的幅频特性。

①测试RC无源低通滤波器的幅频特性。

实验电路如图2.44（a）所示。

实验时，必须在保持正弦波信号输入电压（U1）幅值不变的情况下，逐渐改变其频率，用实验箱提供的数字式真有效值交流电压表（10 Hz＜f＜1 MHz），测量RC滤波器输出端电压U2的值，并把所测的数据记入表2.31。

实验时，应合理选择频率测试点，特别在截止频率两侧的测试点要较密，以得到完整的频率特性曲线。

表2.31　RC无源低通滤波器的幅频特性测量表

②测试RC有源低通滤波器的幅频特性。

实验电路如图2.44（b）所示。

取R=1 kΩ、C=0.01 μF、放大系数K=1。测试方法用与①中相同的方法进行实验操作，并将实验数据记入表2.32中。

表2.32　RC有源低通滤波器的幅频特性测量表

（3）分别测试无源、有源HPF、BPF、BEF的幅频特性，实验步骤、数据记录表格及实验内容自行拟定。

（4）研究各滤波器对方波信号或其他非正弦信号输入的响应（选做，实验步骤自拟）。

6）实验报告

（1）根据实验测量所得的数据，绘制各类滤波器的幅频特性。对于同类型的无源和有源滤波器幅频特性，要求绘制在同一坐标纸上，以便比较，并计算出各自的特征频率、截止频率和通频带。

（2）比较分析各类无源和有源滤波器的滤波特性。

（3）分析在方波信号激励下，滤波器的响应情况（选做）。

7）注意事项

（1）在实验测量过程中，必须始终保持正弦波信号源的输出（即滤波器的输入）电压U1幅值不变，且输入信号幅度不宜过大。

（2）在进行有源滤波器实验时，输出端不可短路，以免损坏运算放大器。

（3）用扫频电源作为激励时，可很快得出实验结果，但必须熟悉扫频电源的操作和使用方法。

8）思考题

（1）试比较有源滤波器和无源滤波器各自的优缺点。

（2）各类滤波器参数的改变，对滤波器特性有何影响。