1）实验目的

（1）用同时分析法观测50 Hz非正弦周期信号的频谱，并与其傅里叶级数各项的频率与系数作比较。

（2）观测基波和其谐波的合成。

2）实验设备

（1）TKSS-C型信号与系统实验箱　　　　一台

（2）YB4340G型双踪示波器　　　　　　一台

3）实验原理

（1）在电子电路系统中最常用的是正弦交流信号，电路的分析以其作为基础。然而，电子技术领域中常遇到另一类交流电，虽然是周期波，却不是正弦量，统称为非正弦周期信号，常见的有方波、锯齿波等，它们对电路产生的影响比单一频率的正弦波复杂得多。

（2）一个非正弦周期波可以用一系列频率与之成整数倍的正弦波来表示。反过来，不同频率的正弦波可以合成一个非正弦周期波。这些正弦波称为非正弦波的谐波分量，其中与非正弦波具有相同频率的成分称为基波或一次谐波，其他成分则根据其频率为基波频率的几倍，就称为几次谐波，其幅度将随谐波次数的增加而减小，直至无穷小。

（3）一个非正弦周期函数可用傅里叶级数来表示，级数各项系数之间的关系可用一个频谱来表示，不同的非正弦周期函数具有不同的频谱图。方波频谱图如图2.40所示。

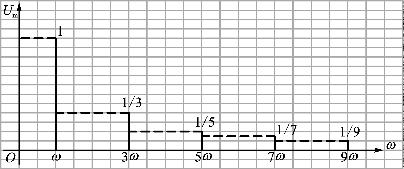
图2.40　方波频谱图

（4）各种不同非正弦周期函数傅里叶级数表达式如下，波形如图2.41所示。

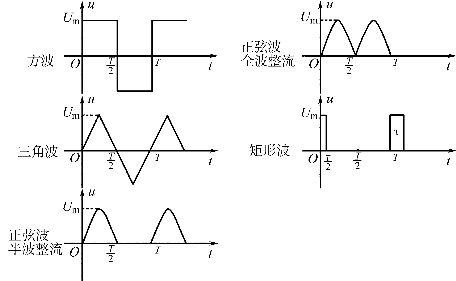
图2.41　几种非正弦周期函数的波形

①方波

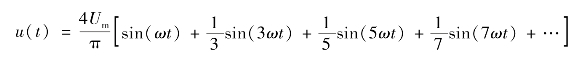
②三角波

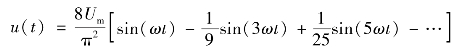
③半波

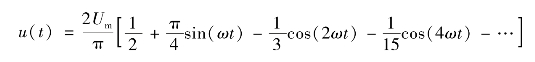
④全波(www.daowen.com)

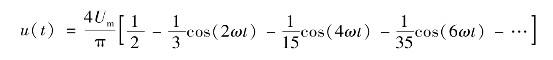
⑤矩形波

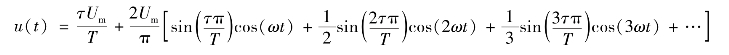
（5）实验电路图如图2.42所示。

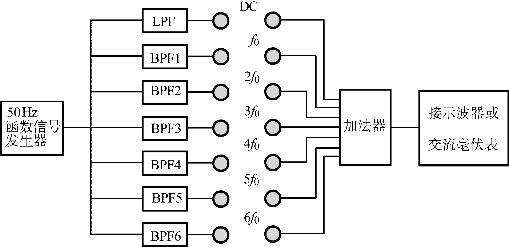
图2.42　信号分解与合成实验装置结构框图

图中LPF为低通滤波器，可分解出非正弦周期函数的直流分量。BPF1～BPF6为调谐在基波和各次谐波的带通滤波器。加法器用于信号的合成。

4）预习要求

在做实验前必须认真复习教材中关于周期性信号傅里叶级数分解的有关内容。

5）实验内容

（1）调节函数信号发生器，使其输出50 Hz的方波信号，并将其接至信号分解实验模块BPF的输入端。也可使用实验箱内提供的50 Hz方波作为输入信号。

（2）将各带通滤波器的输出分别接至示波器，观测各次谐波的频率和幅值，并列表记录之（表格自拟）。

（3）将方波分解所得的基波和三次谐波分量接至加法器的相应输入端，观测加法器的输出波形，并记录。

（4）在（3）的基础上，再将五次谐波分量加到加法器的输入端，观测并记录相加后的波形。

（5）分别将50 Hz单相正弦半波、全波、矩形波和三角波的输出信号接至50 Hz电信号分解与合成模块输入端，观测基波及各次谐波的频率和幅度，并记录。

（6）将50 Hz单相正弦半波、全波、矩形波、三角波的基波和谐波分量分别接至加法器相应的输入端，观测加法器的输出波形，并记录。

6）实验报告

（1）根据实验测量所得的数据，在同一坐标纸上绘制方波及其分解后所得的基波和各次谐波的波形，画出其频谱图。

（2）将方波分解所得的基波和三次谐波的合成波形及基波、三次谐波、五次谐波的合成波形一同绘制在同一坐标纸上，便于比较。

7）思考题

（1）什么样的周期性函数没有直流分量和余弦项？

（2）分析理论合成的波形与实验观测到的合成波形之间误差产生的原因。