1）实验目的

（1）学会用实验方法测定RLC串联谐振电路的电压和电流以及学会绘制谐振曲线。

（2）加深理解串联谐振电路的频率特性和电路品质因数的物理意义。

2）实验原理

含有电感和电容元件的电路，在一定条件下可以呈现电阻性，即整个电路的总电压与总电流同相位，这种现象称为谐振。谐振时，电路的电抗为零，电路的复阻抗Z=R+jX=R，此时阻抗值最小，电路对外呈现纯电阻性，在输入电压Ui为定值时，电路中的电流达到最大值。当电路的参数一定时，调节信号源的频率，可使电路发生谐振（称为变频调谐）；当电源的频率一定时，改变电路的参数L或C的数值也可使电路发生谐振。

在RLC串联谐振电路中，当外加正弦交流电压的频率可变时，电路中的感抗、容抗和电抗都随着外加电源频率的改变而变化，因而电路中的电流也随着频率而变化。将这些物理量随频率而变化的特性绘成曲线，就是它们的频率特性曲线。

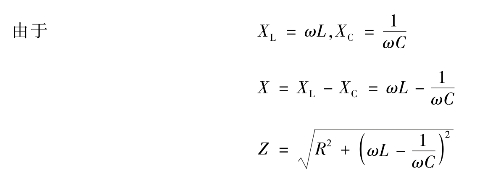
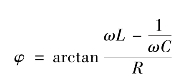
将它们的频率特性曲线绘出，就得到如图2.18所示的一系列曲线，当XL=XC时的频率ω叫做串联谐振频率ω0，这时电路呈谐振状态，谐振角频率为

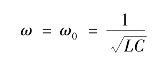
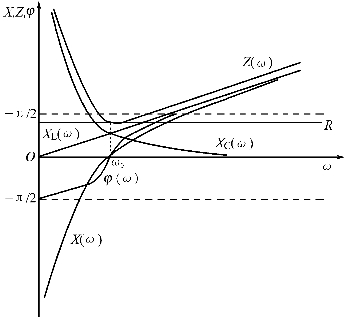
图2.18　串联谐振电路频率特性曲线图

谐振频率为：

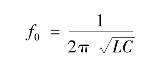
可见谐振频率决定于电路参数L及C，随着频率的变化，电路的性质在ω＜ω0时呈容性；ω＞ω0时呈感性；ω=ω0时，即在谐振点呈纯电阻性。

如维持外加电压U不变，并将谐振时的电流表示为：

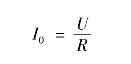
电路的品质因数Q为：

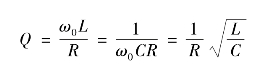
改变外加电压的频率，作出如图2.19所示的电流谐振曲线，它的表达式为：

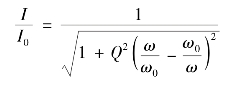(www.daowen.com)

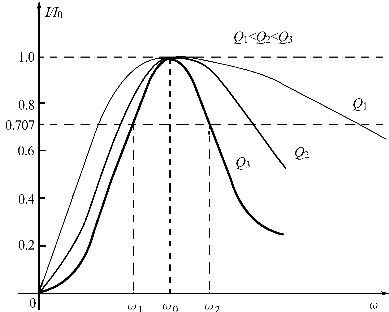
图2.19　不同Q值时的电流谐振曲线

当电路的L及C维持不变，只改变R的大小时，可以作出不同Q值的谐振曲线。Q值越大，曲线越尖锐。在这些不同Q值谐振曲线图上通过纵坐标I/I0=0.707处作一平行于横轴的直线，与各谐振曲线交于两点——ω1及ω2，Q值越大，这两点之间的距离越小。可以证明：

上式说明，电路的品质因数越大，谐振曲线越尖锐，电路的选择性越好，相对通频带（ω2-ω1）/ω0越小，这就是Q值的物理意义。

3）实验内容

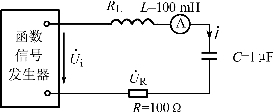
图2.20　串联谐振实验电路图

（1）实验电路如图2.20所示，选C=1 μF，R=100 Ω，L=100 mH（用互感器原边），保持Ui=8 V，调节信号源的频率由小逐渐变大（注意要维持信号源的输出幅度不变），当电路中的电流I的读数为最大时，信号源输出信号的频率即为电路的谐振频率f0。在谐振点两侧，依次各取4～6个测量点，逐点测出电路中的电流I，作出电流谐振曲线。（2）选C=1 μF，R=400 Ω，L=100 mH（用互感器原边），重复步骤（1），完成表2.17。

表2.17　串联谐振测量表

4）实验报告

（1）在坐标纸上绘出两种电阻的电流谐振曲线，并比较上述两种曲线的特点。

（2）计算相对通频带与Q值。

5）思考题

（1）根据实验电路给出的元件参数值，计算电路的谐振频率。

（2）改变电路的哪些参数可以使电路发生谐振，电路中R的数值是否影响谐振频率值？

（3）如何判断电路是否发生谐振？测试谐振点的方案有哪些？

（4）要提高RLC串联谐振电路的品质因数，电路参数应如何改变？

（5）本实验在谐振时，对应的UL与UC是否相等？如有差异，原因何在？