灰色模型以目前确知的信息为基础来对灰色系统进行数学建模，然后通过构建的模型对灰色系统还不确定的部分进行预测。灰色模型可以对历史信息的随机性进行削弱，运用微分拟合法将时间序列转变为微分方程，能够反映系统内机制变动历程的实质，适合用于预测控制。

GM（1，1）模型是最常用的一种灰色预测模型，它将离散的随机数经过依次累加成算子，削弱其随机性，得到较有规律的生成数，然后建立微分方程模型。

设原始序列为

累加序列为

序列X（0），X（1）之间的关系满足：

累加处理的目的，是使新生成的数据序列与原始数据序列相比，平稳性进一步增强而波动性减弱。

对新生成序列建立GM（1，1）白化形式的微分方程：

式中，a称为发展灰数，体现历史序列X（0）与累加生成序列X（1）的变化趋势；b称作内生控制系数，体现数据间的变动关联。

由于所分析的数列是离散的，为了求解a和b，将式离散化，有

背景值公式为

式中，Z（1）（k）称为式（6-3）的背景值；ρ 称为权重系数，[0，1]ρ∈。

假定ρ取0.5，则

将式（6-3）离散化，得

记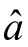=（a，b）T，令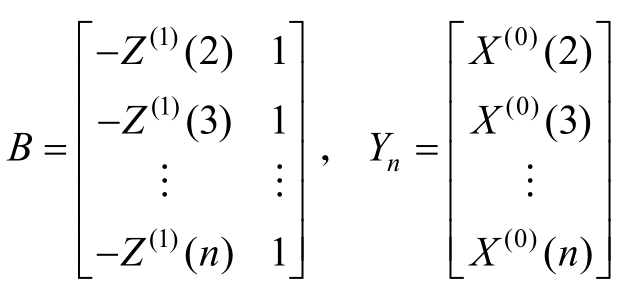

由最小二乘法求解得

将（6-8）代入（6-3）中并令x（1）（1）=x（0）（1），得(www.daowen.com)

该式是x（1）的预测函数。

对（6-9）做累减生成，获取（0）X的灰色预测值为

上式为GM（1，1）模型的预测公式。

若考虑设备状态参数的关联性来做出灰色预测，这样就要用到GM（1，n）模型进行预测。

令为系统的特征数据序列，（i=2，3，…，N）为关联的因素序列：

是的一阶累加生成序列，X（1）=（x（1）（1），x（1）（2），…，x（1）（n）），其中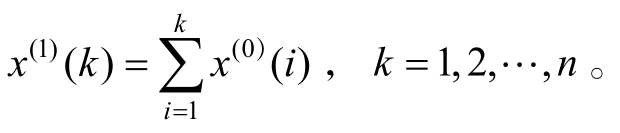

Z（1）为X（1）的紧邻均值生成序列，Z（1）=（z（1）（2），z（1）（3），…，z（1）（n）），其中，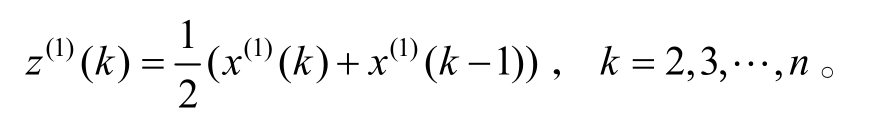

则称

为GM（1，n）模型。

为GM（1，n）模型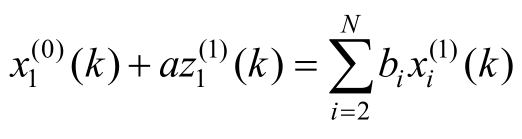的影子方程，也称为白化方程。

设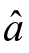=[a，b1，b2，…，bN]T，

则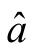=[a，b1，b2，…，bN]T最小二乘估计满足

（1）白化方程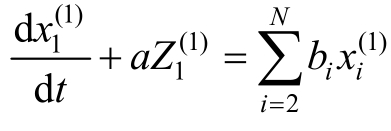的解为

（2）当变化幅度非常小时，则视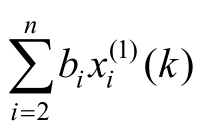为灰常量，于是式（6-15）的时间响应式为

累减还原得