粗糙集通过已有的知识表达系统，利用属性的等价关系来划分论域的范围，得到不区分的等价类，表示为对论域的一种区分能力。通过构建适当的决策表，在保留必要属性的情况下对属性进行约简[27]。

依赖度的定义如下：P，Q∈R，P和Q两者之间相互依赖水平，体现了一个属性对另一个属性的重要程度。属性集Q对于P的依赖程度表示如下：

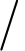式中，表示Q在UInd（P）上的正区域。

（1）当γP=1时，表示Q完全依赖于P，论域所有的研究对象都可以通过属性P划进Q的范围。

（2）当0＜γP＜1时，表示Q部分依赖于P，只有属于正域的研究对象可通过属性P划入Q中。

（3）当γP=0时，表示P和Q之间相互独立，论域中没有对象可以通过P划入Q中。

为研究属性依赖性的差异，引入属性的重要度概念，属性a加入P中，对于分类Uind（Q）的重要程度定义为：

由上可知，属性的重要性不同影响也不同，属性的重要度越大，属性对决策的影响也就越大。

主要流程为：以属性的依赖度作为启发信息，以属性重要度大小依次加入核中；当条件满足后终止，得到属性的约简集合。

步骤如下：(www.daowen.com)

输入：信息系统S=（U，A，V，f），A=C∪U，C∩D≠∅ ，C为条件属性集，D为决策属性集，CoreD（C）表示相对核。

输出：属性约简RedD（C）

（1）令初始条件为：RedD（C）=CoreD（C）。

（2）计算C′=C-redD（C）。

（3）根据C′的结果，计算sig（a，redD（C），D）=γredD（C）∪{a}（D）-γredD（C′）（D），取得最大值的属性a。

（4）假设有多个属性sig（a，redD（C），D）取得最大值，则从中选出与redD（C）的组合值最小的一个属性a。

（5）redD(C)=redD(C)∪{a}，C′=C′-{a}。

（6）当γredD（C）（D）=1，结束；相反，当γredD（C）（D）≠1，跳转到（3）继续。