1.状态指标参量矩阵的建立

传统的主成分分析对设备状态指标的特征提取是直接依据状态监测数据建立指标相关矩阵来进行的，如文献[52]中利用变压器油中溶解气体分析数据、绝缘油试验数据、电气试验数据建立主元分析数学模型，利用主成分分析分别对建立的模型进行求解，提取出主成分中载荷较大的指标，从而达到减少变压器状态评估指标的效果。

分别选取设备状态指标参量，对每个状态指标参量进行量化，可构建指标参量量化矩阵，即X=[X1，X2，…，Xn]。

2.状态数据的预处理

因为所选的变量矩阵量纲往往不同，所以在做主成分分析计算之前应该先消除量纲的影响。消除数据的量纲方法有很多种，最常用的方法是将原始数据进行标准化，即对数据进行如下的变换：

式中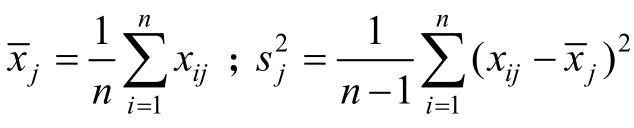，。其中，i=1，2，…，n；j=1，2，…，p。

根据协方差的原理，任何变量对其做标准化变换后，对数据矩阵进行标准化后的变量协方差矩阵就是其相关系数矩阵，标准化后的协方差相关系数是等价的。

3.状态指标参量矩阵求解

求解上述相关系数矩阵，根据，求出该矩阵的特征值以及特征向量，并使其按大小顺序排列λ1≥λ2≥λ3≥…≥λP；分别求出对应于特征值iλ的特征向量ei，其中。选择主成分个数的标准要按照主成分向量的特征值来执行。假设主成分向量的特征值小于某个数值时，就说明它无法解释任何一个指标，所以在选取特征值的时候，应该选择特征值大的因子来作为主成分。

计算累计方差贡献率及确定主成分个数，方差贡献率反映了变量相关性变换后每个主成分所包含的数据信息含量，主成分贡献率越大，该公共因子包含的数据信息含量也就越大，该因子也就越重要。

方差贡献率：(www.daowen.com)

累计方差贡献率：

累计方差贡献率表征了蕴含原始数据信息的多少，一般情况下选择主成分的个数需保证所选择的主成分的累积贡献率应该达到85%以上，可以认为即保留原始数据信息又可以通过主成分来分析解决问题。

4.状态监测指标的特征提取

求取主成分载荷：

式中，λ1，λ2，λ3，…，λm为特征值，α1，α2，α3，…，αm为特征向量

计算各指标变量权重，对选出的m个主成分进行分析，求出主成分中各状态指标参量的权重H，然后按照各状态指标参量的大小进行排名，各指标权重公式如下：

将求出各状态指标参量的权重H进行归一化，到[0，1]，权重越大的状态指标参量说明相关性越强，表示该状态指标参量就在众多指标中越具有代表性。对电力设备状态指标进行特征提取，应当以各状态指标参量的权重结合实际要求，对设备状态关键参量进行特征提取，最后得到设备状态关键指标参量。

根据上述特征提取的原理，电力设备状态指标的特征提取步骤总体流程如图4-3所示。

图4-3　改进主成分分析特征提取流程