如同讨论等温管流一样，应用式（11．52）除以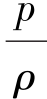得

并利用断面不变时的连续性方程

音速公式

再用等熵过程方程式

所以

将式（a）、式（b）、式（c）代入式（11．66）得

所以

讨论式（11．67）、式（11．68）：

①当l增加，摩阻增加，将引起下列结果：

M＜1，　1－M2＞0，　v增加，　p减小

M＞1，　1－M2＜0，　v减小，　p增加变化率随摩阻的增加而增加。

②M＜1时，摩阻增加，引起速度增加。正如等温管流一样，在管路中间绝不可能出现临界断面。至出口断面上，M只能是M2≤1。

如同等温管路证明（见参考文献［3］）：M＜1，且dv＞0时，则式（11．67）中

1－M2＞0

故

M＜1

③在M＝1处求得的管长就是绝热管流动的最大管长，如管道实长超过最大管长时，与等温管流情况相同。

例11．3 空气温度为16℃，在1at压力下流出，管内径D为10cm的保温绝热管道。上游马赫数M＝0．3，压强比p1／p2＝3．0，求管长，并判断是否为可能的最大管长。(www.daowen.com)

解 ①从马赫数M1求v1

空气k＝1．4，R＝287J／（kg·K），T1＝（273＋16）K＝289K，于是得

②钢管

16℃时，空气ν＝15．3×10－6m2／s

可从莫迪图查得

λ＝0．0175

③应用绝热管流公式（11．65）

上式又可变为

于是

故 l≈45m

④判定是否为最大管长

求M2＝v2／c2，式中v2从绝热伯努利方程及流量ρ1v1求得

ρ1v1＝1．183×102＝120．666

ρ2＝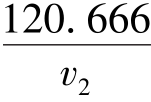

由伯努利方程得

取正值

M2＜1，所以此管长不是可能的最大管长。