上一节研究了速度发生变化时，气流的压强、密度和温度的变化规律，但未讨论速度是在什么情况下发生变化的，以及气流速度变化时，气流形状会发生什么变化，通道的形状应怎样变化才能适应或保证气流速度按要求变化。本节将解决这些问题。

由运动方程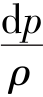＋udu＝0，得

将式（11．47）代入式（11．9），解得

注意到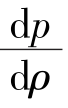＝a2则上式可写成

再将式（11．47）代入上式可得

式（11．47）和式（11．49）建立了压强变化和面积的相对变化同速度相对变化之间的关系。

下面分三种情况进行讨论。

①M＜1，即u＜a

此时，1－M2＞0。从式（11．48）和式（11．49）可以看到，dA与dp同号而与du异号，这说明面积减小时，速度将增大而压强将减小；反之，如果面积增大，则速度减小而压强增大。(www.daowen.com)

②M＞1，即u＞a

此时，1－M2＜0。从式（11．48）和式（11．49）可以看到，dA与dp异号而与du同号。这说明面积增大，则速度增大而压强减小；反之，如果面积减小，则速度减小而压强增大。

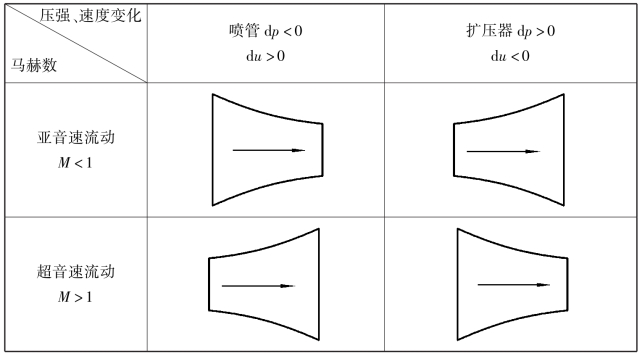
上面两种情况（M＜1或M＞1）下的结果如图11．7所示。在亚音速（M＜1）情况下，使气体加速的喷管和使气体减速的扩压器，其面积变化与速度变化的关系与不可压缩流动情况相同。在超音速（M＞1）情况下，使气体加速的超音速喷管和使气体减速的超音速扩压器，其面积变化与速度变化的关系正好相反，即面积增大速度增大压强减小，面积减小速度减小压强增大。

图11．7　气流参数与通道面积的关系

③M＝1，即u＝a

将式（11．49）改写成

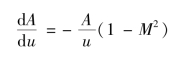
则当M＝1时，上式成为

这意味着通道面积在M＝1时必须通过极小值或极大值。但是，观察图11．7可知，M＝1只能在喉部或最小断面上达到。要将气体从静止加速到超音速（M＞1），首先必须有一个亚音速喷管，然后在适当条件下的最小断面上达到音速。如果在最小断面下游加上一面积渐扩管段，则气流就能继续加速到超音速，此时最小断面称为喉部。但是，超音速实际上不能在超音速扩压器中等熵地减小到亚音速。

由上面的讨论可得这样的结论：一般而言，初始断面为亚音速的收缩形气流不可能达到超音速流动，若要得到超音速气流，必须使收缩气流在其最小断面上达到音速，然后再在扩张通道中继续加速到超音速。