设想存在这样一个参考断面，其上的参数（称为参考状态参数）在整个过程中是不变的。这样的断面能使一元恒定等熵气流的讨论和计算很方便。

（1）第一个参考状态——滞止状态

如果在流动中某一断面上的速度等于零（处于静止或滞止），则此断面上的其他参数就称为滞止参数。一元恒定等熵滞止参数在整个流动过程中不变，因此，它们可作为一种参考状态参数。可证明如下：

记u＝0断面上的其他参数为p0、ρ0、T0、a0、i0另一任意断面上的参数略去下标记为u、p、ρ、T，这里的p、T，称为静压、静温。于是，由式（11．16）可得

因为研究的是完全气体，故i0＝CpT0，且Cp＝常数，所以知道在整个运动过程中T0＝常数（11．27）由式（11．18）和式（11．22）可得

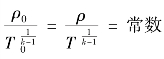
因T0＝常数，故可得

ρ0＝常数　（11．28）

再由式（11．22）或式（11．24）可得

p0＝常数　（11．29）

由上可知，滞止参数在整个运动过程中确是不变的。

为了便于计算，在此推导速度与之间的关系。由式（11．26）可得

再由式（11．18）和式（11．22）可推导得

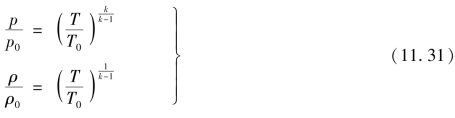
为了计算方便常用表征速度变化的量纲一的数M来表示这些关系式，式（11．30）可改写为

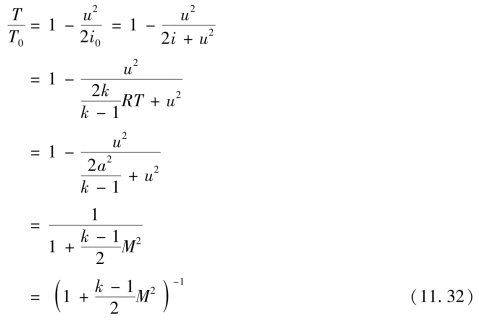
于是

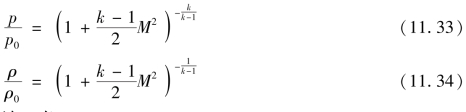
由式（11．30）和式（11．31）可知：当u减小时，p、T均增大，且压强比温度增大得快，密度随u减小而增大；当u增大时，p、T均减小，且压强比温度降低得快，密度随u增大而减小。这种关系反映在图11．5中，因此，在等熵或绝热气流下，随着速度的增加，发生气体膨胀。

例11．1 已知一元恒定等熵空气流某一断面上的速度为142m／s，温度为17℃，压强为1．3×105N／m2。求此气流的滞止温度、滞止压强和滞止密度为多大？（空气的k＝1．4，R＝287J／kg·K）

解 由能量方程

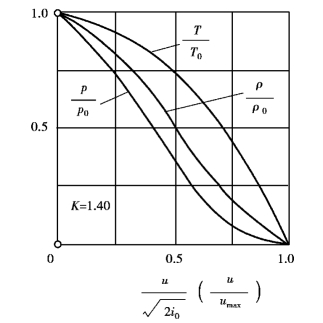
图11．5　一元恒定等熵气流基本特性关系曲线

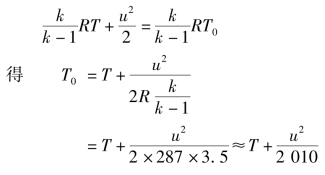
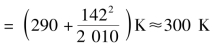
由式（11．31）得

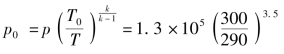
≈1．42×105N／m2

于是，由状态方程可得

（2）第二个参数状态——临界状态(www.daowen.com)

当一元恒定等熵气流中某一断面上的速度等于当地音速时，该断面上的参数就称为临界参数。记u＝a时的压强、密度、温度为p∗、ρ∗、T∗。临界参数在整个运动过程中不变，因此，它们可作为另一种参考状态参数，可证明如下：

因为，故由式（11．24）可得

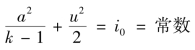
由上式可知，当u增大时，a便减小。当u＝a，并记它们为a∗时，便得

即

由于T0不变，所以a0在整个运动过程中是不变的。由此可知，由于a∗不变，所以T∗在整个运动过程中是不变的。类似滞止状态中的证明过程，可推知ρ∗、p∗在整个运动过程中也是不变的。

由于a∗与a0有确定的关系，即T∗与T0有确定的关系，因而p、ρ、T与临界参数的关系可通过临界参数与滞止参数的关系而求得。

由式（11．35）直接可得

再由式（11．31）可得

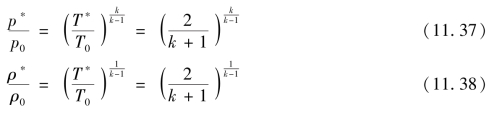
当k＝1．4时，可得

当k＝1．4时，由速度增大，p、ρ、T均减小可推知：

当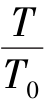＜0．833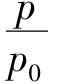＜0．528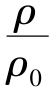，＜0．634时，为超音速流动；

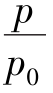当＞0．833，＞0．528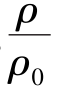，＞0．634时，为亚音速流动。

故式（11．36）至式（11．37）可用作判断一元恒定等熵气流是超音速还是亚音速流动的准则。

（3）第三个参考状态——最大速度状态（极限状态）

如果一元恒定等熵气流某断面上的T＝0，则该断面上的气流速度达到最大值，记为umax。因为T＝0时，p、ρ、a的值均等于零，分子的热运动停止。当然，实际上这是达不到的，但它有理论价值。因为最大速度在整个运动过程中不变，所以它可作为又一种参考状态参数。证明如下：

T＝0即i＝0，于是由式（11．16）得

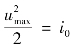
即

或

上式也表明，一元恒定等熵气流中的总能量全部转化为动能时能达到最大速度值。它也是极限状态参数与滞止状态参数的唯一联系公式，因为极限状态参数只有一个，即最大速度umax。

当u＝umax时，易知其相应的压强和密度为

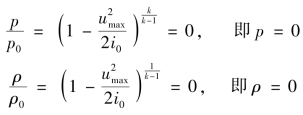
此外，由式（11．40）可得

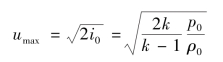
这说明umax决定于i0即T0，而不决定于p0，即滞止压强单独不能影响最大速度的大小。这三个参考状态中，滞止状态和临界状态比较重要。